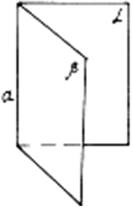
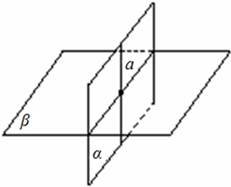
Признак перпендикулярности плоскостей

Если плоскость α проходит через прямую а, которая перпендикулярна другой плоскости β, то такие плоскости перпендикулярны.

Кроме знания этих теорем вам потребуется умение строить искомые в задачах углы и расстояния. Отрезок АН называется перпендикуляром, проведённым из А к плоскости α, точка Н — основание перпендикуляра. М — точка плоскости, отличная от Н. Отрезок АМ — наклонная к плоскости, М — её основание, отрезок НМ — проекция наклонной на плоскость. Перпендикуляр АН меньше наклонной АМ. Длина АН называется расстоянием от точки А до плоскости α.

1. Расстояние между точками A и B можно вычислить:

· как длину отрезка AB, если отрезок AB удается включить в некоторый треугольник в качестве одной из его сторон;

2. Расстояние от точки M до прямой можно вычислить:

· как длину отрезка перпендикуляра, включив этот отрезок в треугольник (трапецию) в качестве одной из высот

3. Расстояние от точки М до плоскости α можно вычислить:

· как расстояние до плоскости α от произвольной точки Р, лежащей на прямой n, которая проходит через точку М и параллельна плоскости α;

· как расстояние до плоскости α от произвольной точки Р, лежащей на плоскости β, которая проходит через точку М и параллельна плоскости α;

· вычисляется по формуле: ρ (M, α) = ρ (M, ABC) = , где треугольник АВС расположен на плоскости α, а объём пирамиды АВСМ равен VABCM. В общем случае рассматривают равенство объемов одной фигуры, выраженные двумя разными способами (метод объёмов);

4.Расстояние между скрещивающимися прямыми можно вычислить:

· как расстояние от любой точки одной из этих прямых до плоскости, проходящую через вторую прямую, параллельно первой прямой;

· как расстояние между двумя параллельными плоскостями, содержащие эти прямые;

· как длину общего перпендикуляра (отрезок, с концами на этих прямых и перпендикулярный каждому из них);

· если ортогональная проекция на плоскость α переводит прямую а в точку А, а прямую b в прямую b 1, то расстояние между скрещивающимися прямыми a и b равно расстоянию от точки А до прямой b 1.

 

Углы

1. Угол между скрещивающимися прямыми ― это угол между параллельными им прямыми, лежащими в одной плоскости.

а и b ― скрещивающиеся прямые. М ― произвольная точка пространства, через которую проведём прямые а 1 || а и b 1 || b, то угол между прямыми (а 1; b 1) и есть искомый угол между а и b.

Угол между скрещивающимися прямыми можно вычислить как угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся.

2. Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость. Искомый угол ∠ АМН.

3. Угол между плоскостями можно вычислить:

· как угол треугольника, если удастся включить линейный угол в некоторый треугольник;

· как угол между прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения;

· как между перпендикулярами к данным плоскостям;

· как угол между плоскостями, параллельными данным плоскостям.

4.Двугранным углом называется фигура, образованная двумя не принадлежащими одной плоскости полуплоскостями, имеющими общую границу ― прямую а. Полуплоскости, образующие двугранный угол называются его гранями, а общая граница этих плоскостей ― ребром двугранного угла.

Двугранный угол, как и плоский угол, измеряется в градусах. Чтобы измерить двугранный угол необходимо на общей прямой выбрать произвольную точку O. В обеих плоскостях через точку O проводятся два луча ОА и ОВ перпендикулярно ребру a. Образованный угол AOB называется линейным углом двугранного угла с ребром a. Таким образом, для измерения угла между двумя пересекающимися плоскостями необходимо измерить линейный угол ∠ AOB.

Опорная задача: Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции: S пр = S ∙ cos α, где S ― площадь многоугольника, лежащего в плоскости p, а S пр (или S 1) ― площадь его ортогональной проекции на плоскость q.

S 1 = S ∙ cos α.