
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные тригонометрические формулыСодержание книги
Поиск на нашем сайте
Тригонометрические формулы суммы и разности двух углов
Тригонометрические формулы двойного угла
Формулы понижения степени
Тригонометрические формулы произведения
Формулы суммы и разности тригонометрических функций sin α + sin β = 2sin sin α – sin β = 2sin cos α + cos β = 2cos cos α – cos β = –2sin Формулы приведения Формул приведения много, а точнее 32. И все формулы надо знать. К счастью существует простое мнемоническое правило, позволяющее быстро воспроизвести любую формулу приведения. Каждая формула связывает между собой либо синус с косинусом, либо тангенс с котангенсом. Причём, первая функция либо меняется на вторую, либо нет. 1. В левой части формулы аргумент представляет собой сумму или разность одного из «основных координатных углов»:
2. В правой части знак перед функцией либо «плюс», либо «минус». Мнемоническое правило Достаточно задать себе два вопроса: 1. Меняется ли функция на кофункцию? Ответ: Если в формуле присутствуют углы 2. Какой знак надо поставить в правой части формулы? Ответ: Знак определяем по левой части. Смотрим, в какую четверть попадает угол, и вспоминаем, какой знак в этой четверти имеет функция, стоящая в левой части. Например, sin( 1) «Меняется функция или нет?»
2) «Знак?» Угол ( Итак, получили формулу, sin( Тригонометрический круг Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое. Он заменяет десяток таблиц. Сколько полезного на этом рисунке! 1. Перевод градусов в радианы и наоборот. Полный круг содержит 360 градусов, или 2π радиан. 2. Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси x, а значение синуса — на оси y. 3. И синус, и косинус принимают значения от –1 до 1. Тригонометрический круг:
1. Значение тангенса угла α тоже легко найти — поделив sinα на cosα. А чтобы найти котангенс — наоборот, косинус делим на синус. 2. Знаки синуса, косинуса, тангенса и котангенса. 3. Синус — функция нечётная, косинус — чётная. 4. Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен 2π. Графики тригонометрических функций На рисунках приведены графики тригонометрических функций: y = sin x, y = cos x, y = tg x, y = ctg x. 1. График функции y = sin x
2. График функции y = cos x
3. График функции y = tg x
4. График функции y = ctg x
Площади плоских фигур Большинство планиметрических задач на экзамене заканчиваются словами «найти площадь…». В 99% таких задач работать в итоге придется с самыми простыми известными плоскими фигурами, а именно находить площадь треугольников, четырехугольников и окружности. На этом занятии мы рассмотрим и повторим все основные формулы нахождения площадей, а также обратим внимание на частные случаи, которые могут существенно облегчить задачу.
Цель урока ― обобщить и систематизировать знания, умения и навыки по нахождению площадей плоских фигур. Сначала мы систематизируем и обобщим знания и умения по теме, затем вы должны будете выполнить несколько типов заданий, которые помогут закрепить материал и легко справиться с задачами такого типа на экзамене.
Треугольник Существует пять основных формул нахождения площади произвольного треугольника:
S = S = S = S = r ∙ p, где r ― радиус вписанной окружности, p ― полупериметр треугольника. S = Как следствия из этих формул, можно отметить следующие частные случаи:
Пример: Найдите площадь треугольника, если известны три его стороны: 5, 9, 12. Решение: Прежде всего определяемся с подходящей формулой нахождения площади. Есть ли среди пяти основных форму та, в которой мы используем три стороны? Да, это формула Герона. Тогда: S = S = Ответ: 4√26.
Параллелограмм
S = a ∙ h, где a ― сторона параллелограмма, h ― высота, проведенная к этой стороне. S = a ∙ b ∙ sin γ, где a, b ― стороны параллелограмма, γ ― величина угла между ними. Как следствия из этих формул, можно отметить следующие частные случаи:
Пример: Стороны параллелограмма равны 1 и √3, а его площадь равна 1,5. Чему равен тупой угол, образованный его сторонами? Решение: Даны стороны и площадь, найти необходимо угол. Подходящая формула: S = a ∙ b ∙ sin γ. Подставим данные из условия задачи: 1.5 = 1√3 ∙ sin γ ⇔ sin γ = Тогда γ =60 или 120. Но в задаче требуется найти тупой угол ⇒ γ = 120. Ответ: 120.
Трапеция
S = Пример: Вычислите среднюю линию трапеции, если ее высота 6 см, а площадь 36 см2. Решение: Зная площадь и высоту трапеции, можем найти полусумму ее оснований, а это и есть средняя линия: S = Ответ: 6 см.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.61 (0.007 с.) |

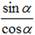 , α≠
, α≠ 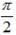 + πn, n є Z
+ πn, n є Z
 , a ≠ πn, n є Z
, a ≠ πn, n є Z
 , n є Z
, n є Z
 , a ≠
, a ≠  + πn, n є Z
+ πn, n є Z
 , a ≠ πn, n є Z
, a ≠ πn, n є Z
 α, β, α + β ≠
α, β, α + β ≠ 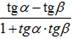 α, β, α + β ≠
α, β, α + β ≠  α ≠
α ≠ 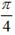 +
+ 
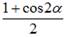
 α ≠
α ≠ 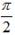 + πn, n є Z
+ πn, n є Z
 (cos(α − β) − cos(α + β))
(cos(α − β) − cos(α + β))
 ∙cos
∙cos  ;
; ∙cos
∙cos  ;
; ∙cos
∙cos  .
. , 2 π и острого угла α, а в правой части аргумент α.
, 2 π и острого угла α, а в правой части аргумент α. — угол вертикальной оси, киваем головой по вертикали: «Да, меняется». Значит в правой части будет cos α.
— угол вертикальной оси, киваем головой по вертикали: «Да, меняется». Значит в правой части будет cos α.





 ⋅ a ⋅ h,где a ― сторона треугольника, h ― высота, проведенная к этой стороне.
⋅ a ⋅ h,где a ― сторона треугольника, h ― высота, проведенная к этой стороне. (формула Герона), где a, b, c ― стороны треугольника, p ― полупериметр треугольника.
(формула Герона), где a, b, c ― стороны треугольника, p ― полупериметр треугольника.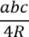 , где a, b, c ― стороны треугольника, R ― радиус описанной окружности.
, где a, b, c ― стороны треугольника, R ― радиус описанной окружности.


 ∙ a 2 ∙ √3
∙ a 2 ∙ √3

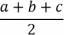 =
=  = 13.
= 13. =
=  = 4√26.
= 4√26.



 .
.
 ∙ h,где a, b ― основания трапеции, h ― высота трапеции.
∙ h,где a, b ― основания трапеции, h ― высота трапеции.


