
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы сокращённого умноженияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
У некоторых людей существует трудности с использованием формул сокращённого умножения. Все эти степени и скобки, внезапно превращающиеся в произведения ― да как это вообще работает? На самом деле, основная причина непонимания как раз и кроется в этом вопросе: «Как это вообще работает?» Простая зубрёжка не всегда даёт свои результаты, в то время как осознание того, откуда появляются эти выражения (что, кстати, совсем несложно, в чём мы сейчас и убедимся) позволяет раз и навсегда расправиться с проблемами в этой теме.
Сейчас мы увидим три основных формулы сокращённого умножения, поймём, почему они называются именно так, докажем их, а затем для каждого случая рассмотрим конкретные примеры.
Возьмём самую распространённую формулу:
a2 – b2 = (a – b)∙(a + b).
Для начала отвлечёмся от математики и попытаемся прочитать левую часть этой формулы. Да-да, вы не ослышались ― именно прочитать, можно даже слегка нараспев и с выражением. У нас есть два числа в квадрате, и мы вычитаем одно из другого. Таким образом, у нас есть разница квадратов (слово «чисел» обычно опускается). Собственно, это и есть формальное название этой формулы.
Теперь давайте взглянем на правую часть. У нас есть произведение двух скобок ― так почему бы не попробовать просто перемножить эти скобки, элемент за элементом?
(a – b)∙(a + b) = a 2 + ab – ba – b 2 = a 2 + ab – ab – b 2 = a 2 – b 2.
Так, постойте. Но это же…как раз и есть левая часть нашего равенства! Неужели, просто раскрыв скобки и приведя подобные слагаемые, мы получили нашу загадочную формулу?
Правильный ответ ― да, так оно и есть! Более того, математически эта формула доказывается именно таким образом. Конечно, это не единственное существующее доказательство* ― но определённо самое простое.
Посмотрим на конкретном примере. Разложим на простые множители x 2 – 4:
x 2 – 4 = (x – 2)∙(x + 2).
Теперь давайте взглянем на другую формулу, которую можно назвать паронимом нашей первой (пароним ― это похожие по звучанию, но различные по смыслу слова):
(a – b)2 = a2 – 2ab + b2.
Я уже вижу возмущение на ваших лицах ― как же так, они же выглядят совсем по-разному! Тем не менее, давайте попробуем прочитать левую часть. Мы вычитаем одно число из другого, а затем возводим получившееся в квадрат. Ещё раз ― вычитание, а затем возведение в степень. Это определённо квадрат разницы (и снова слово «чисел» опускается). Вот теперь и правда похоже, даже несколько пугающе похоже. Как же их различить? Да очень просто ― по смыслу, так же, как мы только что делали с вами вместе. Главное правильно читать математическую (или русскую запись) и понимать, что идёт за чем ― вначале возведение в квадрат и затем вычитание, или наоборот ― вначале вычитание, а затем возведение в квадрат.
Но вернёмся к нашей формуле. Что такое число в квадрате? Это его произведением на самого себя, то есть:
(a – b)2 = (a – b)∙(a – b).
Как и в первом случае, у нас снова есть произведением двух скобок. Так давайте поступим точно так же и почленно перемножим их:
(a – b)∙(a – b) = a 2 – ab – ba + b 2 = a 2 – ab – ab + b 2 = a 2 – 2 ab + b 2.
Вуаля! Снова, как и в предыдущем примере, мы пришли к нужному результату, просто перемножив скобки и приведя подобные слагаемые.
Давайте закрепим успех, использовав эту формулу на конкретном примере. Раскроем скобки (1 – 2 xy)2:
(1 – 2 xy)2 = 1 – 4 xy + 4 x 2 y 2.
И ещё одна формула ― на этот раз внешне очень похожая на вторую, но имеющая другой смысл (в русском языке нет подходящего определения для таких слов. Может, оно и к лучшему):
(a + b)2 = a2 + 2ab + b2.
Вспоминаем, что такое число в квадрате, и опять перемножаем скобки:
(a + b)∙(a + b) = a 2 + ab + ba + b 2 = a 2 + ab + ab + b 2 = a 2 + 2 ab + b 2.
Отлично, вот мы доказали и это выражение! Но как же оно называется? Посмотрим, что у нас есть. Два числа вначале складываются, а потом возводятся в квадрат. Это явно квадрат суммы.
Раскроем скобки и успростим (5 + 3 х)2 – 9 х 2:
(5 + 3 х)2 – 9 х 2 = 25 + 30 х + 9 х 2 – 9 х 2 = 30 х + 25.
Итак, мы с вами успешно разобрались с тремя основными формулами сокращённого умножения, а главное ― поняли, как именно они выводятся. Ещё две формулы (куб разницы и куб суммы, соответственно) ждут вас в домашнем задании, так же как и около десяти примеров для закрепления полученных знаний. Сейчас же давайте ещё раз повторим, что мы узнали:
Успехов!
_____________________________________________________________________________ * Некоторые правила сокращённого умножения были известны ещё около 4 тысяч лет тому назад. Их знали вавилоняне, греки и другие народы древности. Правда, доказывались эти формулы не алгебраически, а геометрически (вообще, практически вся математика в то время сводилась к геометрии). Например, для доказательства разницы квадратов рисовались два квадрата (один в другом), один со стороной a, другой ― со стороной b. Тогда a 2 – b 2 ― это разница площадей квадратов, то есть закрашенная оранжевым часть. (Любопытствующие могут посчитать эту площадь и убедиться, что она равна (a – b)∙(a + b)).
Целые числа Числовые множества Натуральные числа — это числа 1, 2, 3,… Натуральные числа мы используем для счёта, а счёт начинается с единицы. Поэтому ноль не является натуральным числом! Множество натуральных чисел обозначается N. Целые числа — это числа 0, ±1, ±2, ±3,… Натуральные числа являются целыми положительными числами. Множество целых чисел обозначается Z (именно это обозначение мы использовали в тригонометрических уравнениях для записи ответов). Рациональные числа — это всевозможные дроби Множество рациональных чисел обозначается Q. Все натуральные числа являются целыми, все целые — рациональными. То есть N Делимость Понятие делимости относится к целым числам. Определение. Число a делится на число b ≠ 0, если найдётся число c такое, что a = bc. Иногда вместо слова делится говорят делится нацело. Обозначение a Если a делится на b, то число b называется делителем числа a. Например, число 16 имеет пять делителей: это 1, 2, 4, 8 и 16. Признаки делимости: · a делится на 2 ⇔ последняя цифра a есть 0, 2, 4, 6 или 8; · a делится на 5 ⇔ последняя цифра a есть 0 или 5; · a делится на 10 ⇔ последняя цифра a равна 0; · a делится на 3 ⇔ сумма цифр a делится на 3; · a делится на 9 ⇔ сумма цифр a делится на 9. Чётность Определение. Число называется чётным, если оно делится на 2. Число называется нечётным, если оно не делится на 2. Все чётные числа: 0, ±2, ±4, ±6,… Если a чётно, то оно имеет вид a = 2 n. Все нечётные числа: ±1, ±3, ±5,… Если a нечётно, то оно имеет вид a = 2 n + 1. Деление с остатком Любое число a можно разделить с остатком на любое число b ≠ 0. А именно, найдутся два числа q и r такие, что a = b·q + r, причем 0 ≤ r ≤ │ b │. Число q называется частным (иногда, неполным частным), а число r — остатком от деления a на b. Простые числа Всякое число делится на 1 и на само себя. Если натуральное число a не равно 1 и не имеет других натуральных делителей, кроме 1 и a, то такое число a называется простым. Вот первые несколько простых чисел: 2, 3, 5, 7, 11, 13, 17, 19. Число 2 — единственное чётное простое число. Число, не равное 1 и не являющееся простым, называется составным. Всякое число можно разложить на простые множители. Такое разложение единственно с точностью до порядка множителей и называется каноническим разложением. Утверждение о существовании и единственности канонического разложения называется основной теоремой арифметики. Например, 600 = 8 · 25 · 3 = 23 · 52 · 3. Взаимно простые числа Числа называются взаимно простыми, если они не имеют общих делителей кроме 1. Иными словами, числа a и b взаимно просты, если НОД (a, b) = 1, или по-другому дробь
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 777; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.114.190 (0.013 с.) |

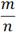 , где m ϵ Z, n ϵ N.
, где m ϵ Z, n ϵ N. Z
Z  b.
b. несократима.
несократима.


