Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равносильные формулы алгебры логикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Две формулы алгебры логики А и В называются равносильными, если они принимают одинаковые логические значения на любом наборе значений входящих в формулы элементарных высказываний. Равносильность формул будем обозначать знаком Например, равносильны формулы:
Формула А называется тождественно истинной (или тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных. Например, тожественно истинны формулы Формула А называется тождественно ложной, если она принимает значение 0 при всех значениях входящих в нее переменных. Например, тождественно ложна формула Ясно, что отношение равносильности рефлексивно, симметрично и транзитивно. Между понятиями равносильности и эквивалентности существует следующая связь: если формулы А и В равносильны, то формула А Важнейшие равносильности алгебры логики можно разбить на три группы. 1. Основные равносильности:
Докажем один из законов поглощения. Рассмотрим формулу 2. Равносильности, выражающие одни логические операции через другие:
Ясно, что равносильности 5 и 6 получаются из равносильностей 3 и 4 соответственно, если от обеих частей последних взять отрицания и воспользоваться законом снятия двойного отрицания. Таким образом, в доказательстве нуждаются первые четыре равносильности. Докажем две из них: первую и третью. Так как при одинаковых логических значениях х и у истинными являются формулы Пусть теперь х и у имеют различные логические значения. Тогда будут ложными эквивалентность будет ложной и конъюнкция
Рассмотрим равносильность 3. Если х и у принимают одновременно истинные значения, то будет истинной конъюнкция х&у и ложным отрицание конъюнкции Пусть теперь хотя бы одна из переменных х или у принимает значение ложь. Тогда будет ложной конъюнкция х&у и истинной ее отрицание. В то же время отрицание хотя бы одной из переменных будет истинным, а поэтому будет истинной и дизъюнкция Следовательно, во всех случаях обе части равносильности 3 принимают одинаковые логические значения. Аналогично доказываются равносильности 2 и 4. Из равносильностей этой группы следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание. Дальнейшее исключение логических операций невозможно. Так, если мы будем использовать только конъюнкцию, то уже такая формула как отрицание х не может быть выражена с помощью операции конъюнкции. Однако существуют операции, с помощью которых может быть выражена любая из пяти логических операций, которыми мы пользуемся. Такой операцией является, например, операция «Штрих Шеффера». Эта операция обозначается символом х|у и определяется следующей таблицей истинности:
Очевидно, имеют место равносильности: 1) 2) х&у Из этих двух равносильностей следует, что всякая формула алгебры логики может быть заменена равносильной формулой, содержащей только операцию «Штрих Шеффера». Отметим, что Аналогично может быть введена операция 3. Равносильности, выражающие основные законы алгебры логики: 1. х& у 2. x 3. х& (у& г) 4. х 5. х& (у 6. х
Докажем последний из перечисленных законов. Если х = 1, то будут истинными формулы х
Пусть теперь х = 0. Тогда х
§ 5. Равносильные преобразования формул Используя равносильности I, II и III групп можно часть формулы или формулу заменить равносильной ей формулой. Такие преобразования формул называются равносильными. Равносильные преобразования используются для доказательства равносильностей, для приведения формул к заданному виду, для упрощения формул. Формула А считается проще равносильной ей формулы В, если она содержит меньше букв, меньше логических операций. При этом обычно операции эквивалентность и импликация заменяются операциями дизъюнкции и конъюнкции, а отрицание относят к элементарным высказываниям. Рассмотрим ряд примеров. 1. Доказать равносильность Используя равносильности I, II и III групп запишем цепочку равносильных формул:
2. Упростить формулу Запишем цепочку равносильных формул:
3. Доказать тождественную истинность формулы
Запишем цепочку равносильных формул:
Алгебра Буля Равносильности III группы говорят о том, что алгебра логики обладает коммутативными и ассоциативными законами относительно операций конъюнкции и дизъюнкции и дистрибутивным законом конъюнкции относительно дизъюнкции, эти же законы имеют место и в алгебре чисел. Поэтому над формулами алгебры логики можно производить те же преобразования, которые проводятся в алгебре чисел (раскрытие скобок, заключение в скобки, вынесение за скобки общего множителя). Но в алгебре логики возможны и другие преобразования, основанные на использовании равносильностей:
Эта особенность позволяет прийти и к далеко идущим обобщениям. Рассмотрим непустое множество М элементов любой природы { x,y,z,... }, в котором определены отношение «=» (равно) и три операции: «+» (сложение), « Коммутативные законы: 1а. х + у = у + х, 1б. х Ассоциативные законы: 2а. х + (у + г) = (х + у) + z, 2б. х Дистрибутивные законы: 3а. (х + у) Законы идемпотентности: 4а. х + х = х, 4б. х Закон двойного отрицания: 5. Законы де-Моргана: 6а. Законы поглощения: 7а. х + (у Такое множество М называется булевой алгеброй. Если под основными элементами х, у, z,... подразумевать высказывания, под операциями «+», « В тех случаях, когда для некоторой системы аксиом удается подобрать конкретные объекты и конкретные соотношения между ними так, что все аксиомы выполняются, говорят, что найдена интерпретация (или модель) данной системы аксиом. Значит, алгебра логики является интерпретацией булевой алгебры. Алгебра Буля имеет и другие интерпретации. Например, если под основными элементами х, у, z,... множества М подразумевать множества, под операциями «+», «
Среди различных интерпретаций булевой алгебры имеются интерпретации и технического характера. Одна из них будет рассмотрена ниже. Как будет показано, она играет важную роль в современной автоматике. Функции алгебры логики Как уже отмечалось, значение формулы алгебры логики полностью зависит от значений входящих в эту формулу высказываний. Поэтому формула алгебры логики является функцией входящих в нее элементарных высказываний. Например, формула трех переменных f(x,y,z). Особенностью этой функции является то обстоятельство, что ее аргументы принимают одно из двух значений: ноль или единицу, и при этом функция также принимает одно из двух значений: ноль или единицу. Определение. Функцией алгебры логики га переменных (или функцией Буля) называется функция га переменных, где каждая переменная принимает два значения: 0 и 1, и при этом функция может принимать только одно из двух значений: 0 или 1. Ясно, что тождественно истинные и тождественно ложные формулы алгебры логики представляют собой постоянные функции, а две равносильные формулы выражают одну и ту же функцию. Выясним, каково число функций n переменных. Очевидно, каждую функцию алгебры логики (как и формулу алгебры логики) можно задать с помощью таблицы истинности, которая будет содержать 2n строк. Следовательно, каждая функция n переменных принимает 2nзначений, состоящих из нулей и единиц. Таким образом, функция n переменных полностью определяется набором значений из нулей и единиц длины 2n.(Общее же число наборов, состоящих из нулей и единиц, длины 2n равно В частности, различных функций одной переменной четыре, а различных функций двух переменных шестнадцать. Выпишем все функции алгебры логики одной и двух переменных. Рассмотрим таблицу истинности для различных функций одной переменной. Она, очевидно, имеет вид:
Из этой таблицы следует, что две функции одной переменной будут постоянными: f1(x)= 1, f4(x) = 0, а f2(x) Таблица истинности для всевозможных функций двух переменных имеет вид:
fi = fi (x,y)
Ясно, что аналитические выражения этих функций могут быть записаны следующим образом:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 3874; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.126.79 (0.013 с.) |

 , а запись A
, а запись A 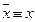 ,
, ,
,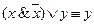 .
.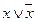 ,
, 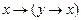 .
.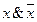 .
.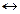 В - тавтология, и обратно, если формула А
В - тавтология, и обратно, если формула А 


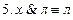


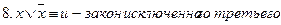


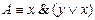 . Если в этой формуле а = 1 то, очевидно,
. Если в этой формуле а = 1 то, очевидно, 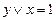 и тогда
и тогда 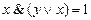 как конъюнкция двух истинных высказываний. Пусть теперь вформуле А x = 0. Но тогда по определению операции конъюнкции будет ложной и конъюнкция
как конъюнкция двух истинных высказываний. Пусть теперь вформуле А x = 0. Но тогда по определению операции конъюнкции будет ложной и конъюнкция 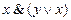 . Итак, во всех случаях значения формулы А совпадают со значениями а, а поэтому А
. Итак, во всех случаях значения формулы А совпадают со значениями а, а поэтому А 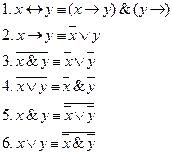
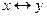 ,
, 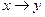 ,
, 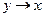 , то истинной будет и конъюнкция
, то истинной будет и конъюнкция 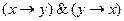 . Следовательно, в этом случае обе части равносильности имеют одинаковые истинные значения.
. Следовательно, в этом случае обе части равносильности имеют одинаковые истинные значения.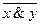 . В то же время будут ложными и
. В то же время будут ложными и  и
и 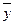 , а поэтому будет ложной и дизъюнкция
, а поэтому будет ложной и дизъюнкция 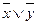 .
.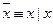 .
. (х|у)|(х|у).
(х|у)|(х|у).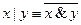 .
.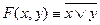 .
. у
у  .
.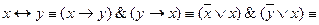
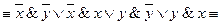
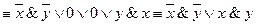 .
.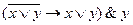 .
.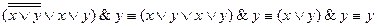 .
.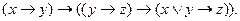 .
.
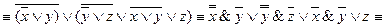
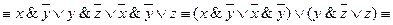
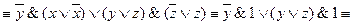
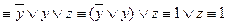
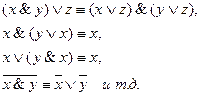
 » (умножение) и «-» (отрицание), подчиняющиеся следующим аксиомам:
» (умножение) и «-» (отрицание), подчиняющиеся следующим аксиомам: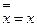 .
.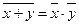 , 6б.
, 6б.  .
.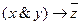 является функцией
является функцией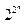 . Значит, число различных функций алгебры логики п переменных равно
. Значит, число различных функций алгебры логики п переменных равно 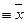 .
.