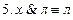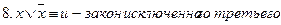Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Высказывания и логические операции над ними. Формулы алгебры логикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Понятие высказывания является основным неопределяемым понятием математической логики. Под высказыванием понимают любое повествовательное предложение, о котором можно сказать истинно оно или ложно в данных условиях места и времени. Логическое значение высказывания «истина» («ложь») обозначается или буквой и, (л) или цифрой 1, (0). Высказывания обычно обозначают малыми латинскими буквами. Отрицанием высказывания а называется высказывание
Конъюнкцией высказываний а,b называется высказывание a Дизъюнкцией высказываний а,b называется высказывание a Импликацией высказываний а,b называется высказывание а Эквивалентностью (или эквиваленцией) высказываний а,b называется высказывание а Таблица истинности для этих логических операций такова:
Все высказывания можно разделить на простые (или элементарные) и составные (или сложные). Всякое сложное высказывание, которое может быть получено из элементарных высказываний посредством применения выше определенных пяти логических операций, называется формулой алгебры логики. Формулы алгебры логики будем обозначать большими латинскими буквами. Логические значения формулы при различных комбинациях значений входящих в нее высказываний можно описать посредством таблицы, которая называется таблицей истинности формулы. Формула А, всегда истинная, называется тождественно истинной формулой или тавтологией и записывается А
Пример 1. Среди следующих предложений выделить высказывания, установить, истинны они или ложны: 1) река Волхов впадает в озеро Ильмень; 2) всякий человек имеет брата; 3) пейте томатный сок!; 4) существует человек, который моложе своего отца; 5) который час?; 6) ни один человек не весит более 1000 кг; 7) 23<5; 8) для всех действительных чисел х и у верно равенство х+у=у+х; 9) х2-7x + 12; 10) x2-7x+ 12 = 0. Решение. Легко видеть, что высказывания 4), 6), 8) - истинные, а высказывания 1), 2), 7) - ложные. Предложения 3), 5), 9), 10) не являются высказываниями. Пример 2. Пусть a - высказывание «Студент Иванов изучает английский язык», b - высказывание «Студент Иванов успевает по математической логике». Дать словесную формулировку высказываний: 1) Решение. а) «Студент Иванов изучает английский язык и не успевает по математической логике»; б) «Если студент Иванов изучает английский язык, то он успевает по математической логике»; в) «Студент Иванов не успевает по математической логике тогда и только тогда, когда он не изучает английский язык». Пример 3. Доставить таблицу истинности для высказывания Решение. Таблица истинности для высказывания
1.1. Какие из следующих предложений являются высказываниями: 1) Москва - столица России; 2) студент физико-математического факультета; 3) 4) Луна есть спутник Марса; 5) а>0. 1.2. Приведите примеры предложений, а) являющихся высказываниями; б) не являющихся высказываниями. 1.3. Верны ли утверждения: 1) сумма корней приведенного квадратного уравнения равна свободному члену; 2) сумма корней любого приведенного квадратного уравнения равна свободному члену; 3) существует приведенное квадратное уравнение, сумма корней которого равна свободному члену? 1.4. Установите, истинно или ложно высказывание: 1) 2) 3) 4) 5) 6) 7) 8) {l,-l,2} 9) { x | x 3+ x 2- x -1 = 0, x 10) 11) { 12) { 1.5. Является ли высказыванием следующее предложение: «Это предложение ложно»? 1.6. Среди следующих высказываний указать элементарные и составные. В составных высказываниях выделить грамматические связки:
1) число 27 не делится на 3; 2) число 15 делится на 5 и на 3; 3) если число 126 делится на 9, то оно делится на 3; 4) число 7 является делителем числа 42; 5) число 1269 делится на 9 тогда и только тогда, когда 18 делится на 9. 1.7. Обозначьте элементарные высказывания буквами и запишите следующие высказывания с помощью символов алгебры логики: 1) 45 кратно 3 и 42 кратно 3; 2) 45 кратно 3 и 12 не кратно 3; 3) 4) 2 5) если число 212 делится на 3 и 4, то оно делится на 12; 6) число 212 - трехзначное и кратно 3 или 4. 1.8. Пусть р и q обозначают высказывания: р - «Я учусь в школе», q - «Я люблю математику». Прочтите следующие сложные высказывания: 1) 1.9. Какие из следующих импликаций истинны: 1) если 2x2 = 4, то 2<3; 2) если 2x2 = 4, то 2>3; 3) если 2x2 = 5, то 2<3; 4) если 2x2 = 5, то 2>3? 1.10. Выясните, в каких случаях приведенные ниже данные противоречивы: 1) a = 1, а & b = 0; 2) a = 1,a 3) а = 1, а & b = 1; 4) а = 1, a 5) a = 0, а & b = 1; 6) а = 0, a 7) а = 0, a&b = 0; 8) а = 0, a 1.11. Пусть x, x', y, у' означают соответственно «7 -простое число», «7 - составное число», «8 - простое число», «8 - составное число»: 1) какие из предложений х&у, х&у', х'&у, х'&у' истинны и какие ложны?; 2) то же с заменой конъюнкции на дизъюнкцию; 3) то же для предложений 1.12. Проверить, не составляя таблиц истинности, являются ли следующие формулы тождественно истинными: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 1.13. Найдите логические значения х и у, при которых выполняются равенства: 1) 1.14. 1) Известно, что импликация х 2) Известно, что эквивалентность х 3) Известно, что х имеет значение 1. Что можно сказать о значениях импликации 4) Известно, что сказать о значениях 1.15. Пусть x = 0, у = 1, z = 1. Определить логические значения нижеследующих сложных высказываний: 1) 2) 3) 4) 5) 6) 1.16. Показать, что логические связки 1.17. 1) Постройте с помощью отрицания и дизъюнкции формулу, таблица истинности для которой совпадала бы с таблицей для импликации. 2) Аналогично этому постройте с помощью отрицания и импликации формулу, таблица для которой совпадает с таблицей для дизъюнкции, ивторую формулу с таблицей, совпадающей с таблицей для конъюнкции. 1.18. Составить таблицы истинности для формул: 1) 2) 3) 4) 5) 6) 7) 8) 1.19. Установить, какие из следующих формул являются тождественно истинными, тождественно ложными: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10)
§ 2. Равносильные формулы алгебры логики Определение. Две формулы алгебры логики А и Б называются равносильными, если онипринимают одинаковые логические значения на любом наборе значений входящих в них высказываний (А Важнейшие равносильности можно разбить на три группы: I. Основные равносильности.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 12529; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.17.171 (0.014 с.) |

 , которое истинно, если а ложно, и ложно, если а истинно. Высказывание
, которое истинно, если а ложно, и ложно, если а истинно. Высказывание  b (а&b), которое истинно, если а и Ъ истинны и ложно, если хотя бы одно из них ложно. Высказывание а
b (а&b), которое истинно, если а и Ъ истинны и ложно, если хотя бы одно из них ложно. Высказывание а 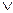 b, которое истинно, если хотя бы одно из высказываний а или 6 истинно, и ложно, если оба они ложны. Читается: «a или b».
b, которое истинно, если хотя бы одно из высказываний а или 6 истинно, и ложно, если оба они ложны. Читается: «a или b». b, которое ложно, если а истинно и b ложно, и истинно во всех остальных случаях. Читается: «Если а, то b».
b, которое ложно, если а истинно и b ложно, и истинно во всех остальных случаях. Читается: «Если а, то b». b, которое истинно, если оба высказывания а и 6 одновременно истинны или ложны, и ложно во всех остальных случаях. Читается: «а тогда и только тогда, когда b».
b, которое истинно, если оба высказывания а и 6 одновременно истинны или ложны, и ложно во всех остальных случаях. Читается: «а тогда и только тогда, когда b». 1. Формула В, всегда ложная, называется тождественно ложной формулой и записывается B
1. Формула В, всегда ложная, называется тождественно ложной формулой и записывается B  ; 2)
; 2)  ; 3)
; 3) 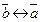 .
.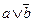 .
.
 ;
; ;
;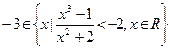 ;
; ;
; ;
; , где P (N)- множество всех подмножеств множества N;
, где P (N)- множество всех подмножеств множества N;

 ;{ x | x 3+ x 2- x -l = 0, x
;{ x | x 3+ x 2- x -l = 0, x  };
};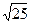 =5 или
=5 или  5;
5; ; 2)
; 2) 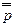 3) p&q; 4) p&
3) p&q; 4) p&  ; 5)
; 5) 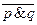 .
. .
. ;
; ;
;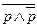 ;
;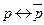 ;
;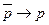 ;
;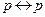 ;
; ;
; ;
;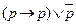 ;
; ;
; ;
; ;
; ;
; .
.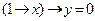 ; 2)
; 2)  .
. и
и 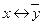 ?
? ;
;  ?
? ;
;  ;
; 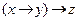 ?
? ;
; ;
; ;
; ;
; ;
; .
. ,
,  ,
,  ,
,  , где л - фиксированное ложное высказывание, имеют ту же таблицу истинности, что и импликация
, где л - фиксированное ложное высказывание, имеют ту же таблицу истинности, что и импликация  ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
;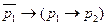 ;
; ;
; ;
; ;
; ;
; ;
;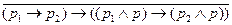 .
. В).
В).