
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приложения алгебры логики в технике (релейно-контактные схемы).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Среди технических средств автоматизации значительное место занимают устройства релейно-контактного действия. Они широко используются в технике автоматического управления, в электронно-вычислительной технике и т.д. Эти устройства (их в общем случае называют переключательными схемами) содержат сотни реле, электронных ламп, полупроводников и электромагнитных элементов. Описание и конструирование таких схем в силу их громоздкости весьма затруднительно. Еще в 1910 году физик П. С. Эренфест указал на возможность применения аппарата алгебры логики при исследовании релейно-контактных схем (РКС). Однако его идеи стали реализовываться значительно позже, когда создание общей теории конструирования РКС стало остро необходимым. Использование алгебры логики в конструировании РКС оказалось возможным в связи с тем, что каждой схеме можно поставить в соответствие некоторую формулу алгебры логики, и каждая формула алгебры логики реализуется с помощью некоторой схемы. Это обстоятельство позволяет выявить возможности заданной схемы, изучая соответствующую формулу, а упрощение схемы свести к упрощению формулы. С другой стороны, до построения схемы можно заранее описать с помощью формулы те функции, которые схема должна выполнять. Рассмотрим, как устанавливается связь между формулами алгебры логики и переключательными схемами. Под переключательной схемой понимают схематическое изображение некоторого устройства, состоящего из следующих элементов: 1) переключателей, которыми могут быть механические действующие устройства (выключатели, переключающие ключи, кнопочные устройства и т. д.), электромагнитные реле, электронные лампы, полупроводниковые элементы и т.п.; 2) соединяющих их проводников; 3) входов в схему и выходов из нее (клемм, на которые подается электрическое напряжение). Они называются полюсами схемы. Сопротивления, конденсаторы и т.д. на схемах не изображаются. Переключательной схемой принимается в расчет только два состояния каждого переключателя, которые называют «замкнутым» и «разомкнутым». Рассмотрим простейшую схему, содержащую один переключатель Р и имеющую один вход А и один выход В. Переключателю Р поставим в соответствие высказывание р, гласящее: «Переключатель Р замкнут». Если р истинно, то импульс, поступающий на полюс А, может быть снят на полюсе В без потери напряжения. Будем в этом случае говорить, что схема проводит ток. Если р ложно, то переключатель разомкнут, и схема тока не проводит или на полюсе В снимается минимальное напряжение при подаче на полюс А максимального напряжения. Если принять во внимание не смысл высказывания, а только его значение, то можно считать, что любому высказыванию может быть поставлена в соответствие переключательная схема 1.
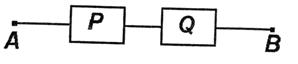
Схема 1. Формулам, включающим основные логические операции, также могут быть поставлены в соответствие переключательные схемы. Конъюнкция двух высказываний р и q будет представлена двухполюсной схемой с последовательным соединением двух переключателей Р и Q (схема 2).
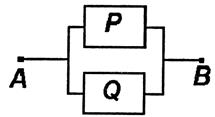
Схема 2. Эта схема пропускает ток тогда и только тогда, когда истинны и р, и q одновременно, то есть истинна конъюнкция р& q. Дизъюнкция двух высказываний р и q изобразится двухполюсной схемой с параллельным соединением двух переключателей Р и Q (схема 3).
Схема 3. Эта схема пропускает ток в случае, если истинно высказывание р или истинно высказывание д, то есть истинна дизъюнкция p Если высказывание р есть отрицание высказывания р, то тождественно истинная формула р
Схема 4.
Схема 5. Из схем 1, 2 и 3 путем последовательного и параллельного их соединения могут быть построены новые двухполюсные переключательные схемы, которые называют П-схемами. Как было показано, всякая формула алгебры логики путем равносильных преобразований может быть представлена в виде формулы, содержащей только две операции: конъюнкцию и отрицание или дизъюнкцию и отрицание. Из этого следует, что всякая формула алгебры логики может быть изображена П-схемой и, обратно, для любой П-схемы может быть записана формула, которая изображается этой схемой. Пример 1. Формуле
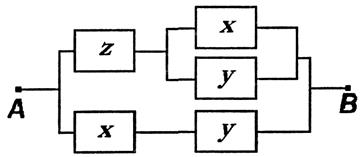
Схема 6. Пример 2. Для П-схемы 7
Схема 7. соответствующая формула алгебры логики имеет вид:
Упростим эту формулу следующим образом:
Последней формуле соответствует П-схема 8:
Схема 8. Из примера 2 следует, что для некоторых РКС путем равносильных преобразований соответствующей формулы алгебры логики можно получить РКС, содержащую меньшее число переключателей. Проблема решения этой задачи носит название проблемы минимизации. Приведем пример построения РКС по заданным условиям с оценкой числа контактов. Пример 3. Построить контактную схему для оценки результатов некоторого спортивного соревнования тремя судьями при следующих условиях: судья, засчитывающий результат, нажимает имеющуюся в его распоряжении кнопку, а судья, не засчитывающий результат, кнопки не нажимает. В случае, если кнопки нажали не менее двух судей, должна загореться лампочка (положительное решение судей принято простым большинством голосов). Решение. Ясно, что работа нужной РКС описывается функцией Буля трех переменных F(x, у, z), где переменные высказывания х, у, z означают: х - судья х голосует «за», у - судья у голосует «за», z - судья г голосует «за». Таблица истинности функции F(x, у, z), очевидно, имеет вид:
В связи с этим СКНФ формулы (функции) F(x,y,z) запишется в виде
А этой формуле соответствует РКС, изображенная на схеме 7, которая содержит двенадцать переключателей. Но как было показано, в результате равносильных преобразований формула F(x, у, z) может быть приведена к виду:
которому соответствует РКС, изображенная на схеме 8, содержащей пять переключателей.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1851; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.40.234 (0.01 с.) |


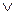 q.
q.

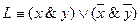 соответствует схема 6:
соответствует схема 6: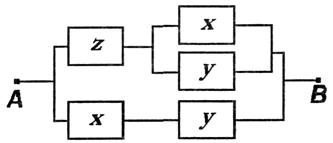

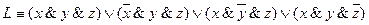 .
.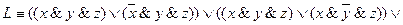
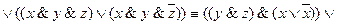
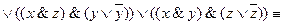
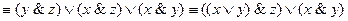 .
.
 .
.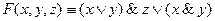 ,
,


