
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементарные функции алгебры логикиСодержание книги Поиск на нашем сайте ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
Пример 2.2 Рассмотрим несколько функций двух переменных (табл.2.7).
Таблица 2.7
Покажем, что (х 1& x 2) существенно зависит от х 1. Рассмотрим наборы (0,1) и (1,1), здесь a 2=1, f (0, a 2)=0 и не равно f (1, a 2)=1. Покажем, что х 2 – тоже существенная переменная. Рассмотрим наборы (1,0) и (1,1). Здесь a 1=1, f (1,0)=0 и не равна f (1,1)=1. Для функции f 3(x 1, x 2) покажем, что х 2 – фиктивная переменная, т.е. надо показать, что не существует наборов (a 1,0) и (a 1,1) таких, что f 3(a 1,0) Для функции f 15 x 1 и x 2 являются фиктивными переменными. x 1–фиктивная переменная, так как существует набор (0, a 2) и (1, a 2), таких, что f (0, a 2)¹ f (1, a 2). Если a 2=0, то f (0,0)= f (1,0)=1, если a 2=1, тогда f (0,1)= f (1,1)=1. Аналогично доказывается, что Пусть хi является фиктивной переменной для функции f (x 1,..., xi,..., xn). Тогда ее можно удалить из таблицы истинности, вычеркнув все строки вида (a 1,... ai– 1, 1, ai +1,... an) или, наоборот, все строки вида (a 1,..., ai– 1, 0, ai +1,... an) и столбец для переменной хi. При этом получим таблицу для некоторой функции g (x 1,..., xi –1, xi +1,... xn). Будем говорить, что функция g (x 1,... xi –1, xi +1,... xn) получена из функции f (x 1,..., x i,... xn) путем удаления фиктивной переменной хi или f получена из g путем введения фиктивной переменной хi (табл.2.8). Определение 2.4. Функции f 1 и f 2 называются равными, если f 2 можно получить из f 1 путем добавления или удаления фиктивной переменной.
Пример 2.3 Таблица 2.8
Вычеркнули строки типа (a,1), т.е. (0,1) и (1,1) и столбец для х 2. Получили f 3(x 1 x 2) = g (x 1) = x 1. Пример 2.4 Пусть функция g (x 1 x 2) задана табл. 2.9 и существенно зависит от обеих переменных. Таблица 2.9
Построим функцию f (x 1, x 2, x 3), которая получается из g (x 1, x 2) введением фиктивной переменной х 3 (табл. 2.10). Таблица 2.10
К наборам (х 1, х 2) мы добавим х 3=0, получим наборы вида (a 1, a 2,0), на этих наборах функцию f положим равной g (a 1, a 2), затем добавим наборы вида (a 1, a 2,1), функцию f (a 1, a 2,1) положим равной g (a 1, a 2). Особую роль играют константы 0 и 1, которые не имеют существенных переменных и которые можно рассматривать как функции от пустого множества переменных.
2.2. Формульное задание функции алгебры логики
Дадим индуктивное определение формулы над множеством. Это определение несколько сложное по форме, но будет полезно в дальнейшем. С индуктивным определением мы встречались в математическом анализе при определении n -го дифференциала dnf (x): было введено понятие первого дифференциала df (x), а затем n -й дифференциал определялся как первый дифференциал от d (n –1) f (x).
Определение 2.5. Пусть М Ì P 2, тогда: 1) каждая функция f (x 1,..., x n)Î M называется формулой над M; 2) пусть g (x 1,..., xm)Î M, G 1,..., Gm – либо переменные, либо формулы над M. Тогда выражение g (G 1... Gn) – формула над M. Формулы будем обозначать заглавными буквами: N [ f 1,..., fs ], имея в виду функции, участвовавшие в построении формулы, или N (х 1,..., xk), имея в виду переменные, вошедшие в формулу. Gi , формулы, участвовавшие в построении g (G 1,..., Gn), называются подформулами.
Пример 2.5. Пусть N ={(x 1& x 2),(x 1Ú x 2),(` x)}, тогда ((х 1& х 2)Ú х 3) – формула над N. Сопоставим каждой формуле N (x 1,..., xn) функцию f (x 1,..., xn)Î P 2. Сопоставление будем производить в соответствии с индуктивным определением формулы. 1) Пусть N (x 1,..., xn)= f (x 1,..., xn), тогда формуле N (x 1,..., xn) сопоставим функцию f (x 1,..., xn). 2) Пусть N (x 1,..., xn)= g (G 1,..., Gm), где каждое Gi – либо формула над M, либо переменная, тогда по индуктивному предположению каждому Gi сопоставлена либо функция fi Î P 2, либо переменная хi, которую можно считать тождественной функцией. Таким образом, каждой формуле Gi сопоставлена функция fi ( Множество всех формул над M обозначим через < M >.
Определение 2.6. Две формулы N и D из < M > называются равными N = D или эквивалентными N ~ D, если функции, реализуемые ими, равны.
Упрощение записи формул 1) внешние скобки можно опускать; 2) приоритет применения связок возрастает в следующем порядке: ~, 3) связка ־ над одной переменной сильнее всех связок; 4) если связка ־ стоит над формулой, то сначала выполняется формула, затем отрицание; 5) если нет скобок, то операции ~ и
Пример 2.6. Доказать эквивалентность формул (табл. 2.11). (
Таблица 2.11
Пример 2.7 Упростим формулы: 1. x 2 x 3Ú x 1 2. x 1Ú
Принцип двойственности
Определение 2.7. Функция f *(x 1,..., xn) называется двойственной к функции f (x 1,..., xn), если f *(x 1,..., xn) = Пример 2.8. Покажем с помощью таблицы истинности (табл. 2.13) что константа 0 двойственна к 1.
Таблица 2.13
Функции f (x) = x и g (x) = так как f *(0)= Таблица 2.14
Определение 2.8. Если f *(x 1,..., xn) = f (x 1,..., xn), то f (x 1,..., xn) называется самодвойственной. Если f *– самодвойственна, то
Пример 2.9. Покажем, что f (x 1, x 2, x 3)= x 1Å x 2Å x 3 – самодвойственна (табл. 2.15). Таблица 2.15
Пример 2.10. Покажем, что функция х1Úх2 двойственна к x1&x2, функция х1
Таблица 2.16
Теорема 2.1. О двойственных функциях Если f * двойственна к f, то f двойственна к f *. Доказательство. f *(x 1,..., xn) = Предположим, что функция задана формулой. Можно ли найти по этой формуле двойственную функцию? Ответ на этот вопрос дает следующая теорема.
Теорема 2.2. О принципе двойственности Пусть функция h (x 1,..., xn) реализована формулой h (x 1,..., xn) = = g (G 1,..., Gm) = g (f 1(x 1,..., xn),..., fm (x 1,..., xn)), где какие-то переменные могут быть фиктивными. Тогда h *(x 1,..., xn) = g *(f 1*(x 1,..., xn),..., fm *(x 1, …, xn)), это означает, что если функция задана некоторой формулой, то, чтобы получить двойственную функцию, надо в этой формуле все знаки функций заменить на двойственные: 0 на 1, 1 на 0. Доказательство. h *(x 1,..., xn) = (x 1,..., xn)), что и требовалось доказать. Если функция h (x 1,..., xn) реализуется формулой N [ f 1,..., fn ], то формулу, полученную из N заменой fi, входящих в нее, на fi * и реализующую функцию h *(x 1,..., xn), будем называть двойственной и обозначать N *(x 1,..., xn). Пример 2.11. Построить формулу, реализующую f *, если f = =((x Найдем (x Å y)* и (x Таблица 2.17
Из табл. 2.17 видно, что (x По принципу двойственности f *= Тогда f = (f *)* = [ z (x Å y)]* = z Ú(x ~ y).
Примеры использования теоремы Поста 1.Покажем, что система функций { f 1 = x 1 x 2, f 2 =0, f 3 =1, f 4 = = x 1Å x 2Å x 3} полна в Р 2. Составим табл. 2.23, которая называется критериальной
Таблица 2.23
Таблица 2.24
Из табл. 2.24 видно, что какой бы класс мы ни взяли, всегда есть функция из данной системы, которая в этот класс не входит. Можно сформулировать следующее правило: для того чтобы система функций была полна, необходимо и достаточно, чтобы в каждом столбце критериальной таблицы был хотя бы один «минус». Отметим еще одно обстоятельство, касающееся приведенной системы. Какую бы функцию из этой системы мы ни удалили, система станет неполной, действительно, { f 2, f 3, f 4}Ì L, { f 1, f 3, f 4}Ì T 1, { f 1, f 2, f 4}Ì T 0, { f 1, f 2, f 3}Ì M. 2. Мы знаем, что система { x 1| x 2} полна в Р 2. Какова для нее критериальная таблица? x 1| x 2=
Таблица 2.25
3. Составим критериальную таблицу для другой полной системы функций из Р2: {0, 1, x 1 x 2, x 1Å x 2} (табл.2.26).
Таблица 2.26
Согласно критериальной таблице, полной является и система {1, x 1 x 2, x 1Å x 2}. Константа 0 введена в эту систему для удобства, тогда мы можем записать полином Жегалкина в виде, где а 4. Выясним, полна ли система Таблица 2.27
Определение 2.15. Система функций { f 1,..., fs,...} называется базисом в Р 2,если она полна в Р 2, но любая ее подсистема не будет полной. Например, система функций { x 1& x 2, 0, 1, x 1
ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
Элементарные функции алгебры логики
Обозначения: E 2={0,1}; Е Определение 2.1. Функцией алгебры логики называется отображение Е Так как множество Е
Пример 2.1. Пусть n =2, тогда Е Тем самым задана функция, для которой мы будем использовать стандартное обозначение f (x 1, x 2), записывая эту функцию в виде таблицы 2.1. Таблица 2.1
Здесь x 1 и x 2 обозначают названия столбцов, а f – символ, обозначающий отображение. Следует обратить внимание, что функции f (x 1, x 2) и f (y 1, y 2) задают одно и то же отображение и их таблицы отличаются только названиями столбцов.
Определение 2.2. Таблица, задающая функцию f (x 1, x 2,..., xn), называется таблицей истинности для этой функции. Рассмотрим функции одной переменной. Их будет всего 4, они задаются таблицами истинности 2.2–2.5.
Таблица 2.2
Функция называется константой 0, записывается f 0(x)
Таблица 2.3
Функция называется тождественной, записывается f 1(x)= x.
Таблица 2.4
Функция называется «не x» и записывается f 2 (x)=
Функция записывается f 3(x) Рассмотрим функции двух переменных f (x 1, x 2). Функции двух переменных определены на множестве Е Таблица 2.6
Некоторые из этих функций носят специальные названия и играют такую же роль, как элементарные функции в анализе, поэтому называются элементарными функциями алгебры логики. Перечислим их. 1) f 1(x 1, x 2) = (x 1& x 2), читается «конъюнкция х 1 и х 2», иногда вместо знака & употребляют знак 2) f 6(x 1, x 2) = (x 1Å x 2) – сложение х 1 и х 2 по модулю два, иногда пишут (х 1+ х 2) mod 2. 3) f 7(x 1, x 2) = (x 1Ú x 2), читается «х 1 дизъюнкция х 2», она совпадает с max(x 1, x 2), ее называют логическим сложением. 4) f 8(x 1, x 2) = (x 1 5) f 9(x 1, x 2) = (x 1~ x 2), читается «х 1 эквивалентно х 2». 6) f 13(x 1, x 2) =(x 1 7) f 14(x 1, x 2) = (x 1| x 2), читается «х 1 штрих Шеффера х 2», она является отрицанием конъюнкции. Cимволы Рассмотрим функцию f (x 1... xn), где (x 1... xn)Î Е С ростом n число Р 2(n) быстро растет: P 2(1)=4, P 2(2)=16, P 2(3)=256, P 2(4)=65536. При больших n табличный способ задания функций становится неприемлемым, используется формульное задание функций. Но прежде чем ввести понятие формулы, дадим определение существенной переменной.
Определение 2.3. Функция f (x 1,..., xi –1, xi, xi +1,..., xn) существенно зависит от хi, если существуют такие значения a 1,... ai –1, ai +1,... an переменных x 1,... xi –1, xi +1,... xn, что f (a 1,... ai –1, 0, ai +1... an)¹ f (a1... ai –1, 1, ai +1... an). Тогда переменная хi называется существенной переменной. В противном случае хi называется фиктивной переменной.
Пример 2.2 Рассмотрим несколько функций двух переменных (табл.2.7).
Таблица 2.7
Покажем, что (х 1& x 2) существенно зависит от х 1. Рассмотрим наборы (0,1) и (1,1), здесь a 2=1, f (0, a 2)=0 и не равно f (1, a 2)=1. Покажем, что х 2 – тоже существенная переменная. Рассмотрим наборы (1,0) и (1,1). Здесь a 1=1, f (1,0)=0 и не равна f (1,1)=1. Для функции f 3(x 1, x 2) покажем, что х 2 – фиктивная переменная, т.е. надо показать, что не существует наборов (a 1,0) и (a 1,1) таких, что f 3(a 1,0) Для функции f 15 x 1 и x 2 являются фиктивными переменными. x 1–фиктивная переменная, так как существует набор (0, a 2) и (1, a 2), таких, что f (0, a 2)¹ f (1, a 2). Если a 2=0, то f (0,0)= f (1,0)=1, если a 2=1, тогда f (0,1)= f (1,1)=1. Аналогично доказывается, что Пусть хi является фиктивной переменной для функции f (x 1,..., xi,..., xn). Тогда ее можно удалить из таблицы истинности, вычеркнув все строки вида (a 1,... ai– 1, 1, ai +1,... an) или, наоборот, все строки вида (a 1,..., ai– 1, 0, ai +1,... an) и столбец для переменной хi. При этом получим таблицу для некоторой функции g (x 1,..., xi –1, xi +1,... xn). Будем говорить, что функция g (x 1,... xi –1, xi +1,... xn) получена из функции f (x 1,..., x i,... xn) путем удаления фиктивной переменной хi или f получена из g путем введения фиктивной переменной хi (табл.2.8). Определение 2.4. Функции f 1 и f 2 называются равными, если f 2 можно получить из f 1 путем добавления или удаления фиктивной переменной.
Пример 2.3 Таблица 2.8
|

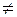 f 3(a 1,1). Пусть a 1=0, т.е. рассмотрим наборы (0,0) и (0,1), f (0,0)= f (0,1)=0. Пусть a 1=1, но f (1,0)= f (1,1)=1.
f 3(a 1,1). Пусть a 1=0, т.е. рассмотрим наборы (0,0) и (0,1), f (0,0)= f (0,1)=0. Пусть a 1=1, но f (1,0)= f (1,1)=1. – тоже фиктивная переменная.
– тоже фиктивная переменная. ), причем {
), причем { 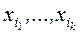 }Í{ x 1,..., x n}, так как в формуле N (x 1,..., xn) перечислены все переменные, участвовавшие в построении формулы. Можно считать, что все функции fi зависят от переменных (x 1,..., xn), причем какие-то переменные могут быть фиктивными. Тогда N (x 1,..., xn) = g (G 1,..., Gm) = g (f 1(x 1,..., xn),..., fm (x 1,.., xn)). Сопоставим этой формуле функцию h (x 1,..., xn) следующим образом: пусть (a 1,..., an) – произвольный набор переменных (x 1,..., xn). Вычислим значение каждой функции fi на этом наборе, пусть
}Í{ x 1,..., x n}, так как в формуле N (x 1,..., xn) перечислены все переменные, участвовавшие в построении формулы. Можно считать, что все функции fi зависят от переменных (x 1,..., xn), причем какие-то переменные могут быть фиктивными. Тогда N (x 1,..., xn) = g (G 1,..., Gm) = g (f 1(x 1,..., xn),..., fm (x 1,.., xn)). Сопоставим этой формуле функцию h (x 1,..., xn) следующим образом: пусть (a 1,..., an) – произвольный набор переменных (x 1,..., xn). Вычислим значение каждой функции fi на этом наборе, пусть  (a 1,..., an)= bi, затем найдем значение функции g (x 1,..., xm) на наборе (b 1,..., bm) и положим h (a 1,..., an) = g (b 1,..., bm) = g (f 1(a 1,..., an),..., fm (a 1,..., an)). Так как каждое fi (x 1,..., xn) есть функция, то на любом наборе (a 1,..., an) она определяется однозначно, g (x 1,..., xm) – тоже функция, следовательно, на наборе (b 1,..., bn) она определяется однозначно, h (x 1,..., xn) есть функция, определенная на любом наборе (a 1,..., an).
(a 1,..., an)= bi, затем найдем значение функции g (x 1,..., xm) на наборе (b 1,..., bm) и положим h (a 1,..., an) = g (b 1,..., bm) = g (f 1(a 1,..., an),..., fm (a 1,..., an)). Так как каждое fi (x 1,..., xn) есть функция, то на любом наборе (a 1,..., an) она определяется однозначно, g (x 1,..., xm) – тоже функция, следовательно, на наборе (b 1,..., bn) она определяется однозначно, h (x 1,..., xn) есть функция, определенная на любом наборе (a 1,..., an). , Ú,&;
, Ú,&; &(х 2Å x 3))~(
&(х 2Å x 3))~( ).
).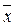 2 x 3 = x 3(x 2Ú x 1
2 x 3 = x 3(x 2Ú x 1 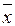 2) = x 3((x 2Ú x 1)&(x 2Ú
2) = x 3((x 2Ú x 1)&(x 2Ú 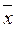 1 x 2Ú
1 x 2Ú  1
1  2 x 3Ú
2 x 3Ú 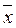 1
1 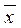 2 x 3 x 4= x 1Ú
2 x 3 x 4= x 1Ú 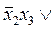
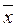 1
1 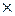
 2
2 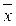 2
2 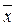 3 х 4)= x 1Ú(x 2Ú x 3)Ú(
3 х 4)= x 1Ú(x 2Ú x 3)Ú(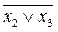 ) x 4= = x 1Ú(x 2Ú х 3Ú(
) x 4= = x 1Ú(x 2Ú х 3Ú(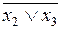 ))(x 2Ú x 3Ú x 4) = x 1Ú x 2Ú x 3Ú x 4.
))(x 2Ú x 3Ú x 4) = x 1Ú x 2Ú x 3Ú x 4.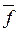 (
(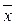 1,...,
1,...,  (1).
(1).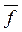 (
(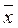 1,...,
1,..., 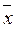 n) = f (x 1,..., xn), т.е. на противоположных наборах функция принимает противоположные значения.
n) = f (x 1,..., xn), т.е. на противоположных наборах функция принимает противоположные значения.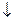 х2 двойственна к функции x1|x2 (табл. 2.16).
х2 двойственна к функции x1|x2 (табл. 2.16). (
(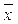 1,...,
1,...,  (
(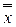 1,...,
1,..., 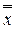 n) = f (x 1,.., xn).
n) = f (x 1,.., xn).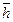 (
( (f 1(
(f 1( (
(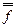 1(
1(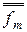 (
(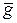 ((
((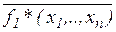 ),..., ((
),..., (( ) = g *(f 1*(x 1,..., xn),..., fm *
) = g *(f 1*(x 1,..., xn),..., fm *
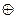 y)*= x ~ y =
y)*= x ~ y = 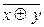 = x
= x  , (x
, (x  y)* =
y)* = 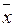 y, x
y, x  y =
y = 
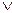 y.
y.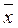 yz
yz 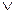 (
(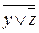 (x
(x 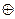 1))=
1))= 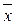 yz
yz 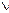
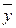 z (x
z (x 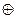 1)= = z (
1)= = z ( y Ú
y Ú 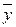 (x Å z Å1))= z (
(x Å z Å1))= z (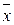 y Ú
y Ú  ))= = z
))= = z 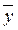 x Å z
x Å z 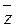 ) = z (
) = z (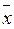 y Ú x
y Ú x 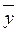 ) = z (x Å y).
) = z (x Å y). = x 1 x 2Å1 (табл.2.25).
= x 1 x 2Å1 (табл.2.25). равны 0, если члены х
равны 0, если члены х  х
х  ... х
... х  в полиноме отсутствуют.
в полиноме отсутствуют. . Составим критериальную таблицу, очевидно,
. Составим критериальную таблицу, очевидно,  . Чтобы показать, что
. Чтобы показать, что 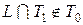 , достаточно найти одну функцию
, достаточно найти одну функцию  и
и  . Возьмем
. Возьмем  , удовлетворяющую требуемым условиям. Если f
, удовлетворяющую требуемым условиям. Если f 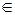 S \ T 0, то f (0,..., 0) = 1, f (1,..., 1)=0, следовательно, f
S \ T 0, то f (0,..., 0) = 1, f (1,..., 1)=0, следовательно, f  M, f
M, f  x 2 x 3
x 2 x 3  T 1
T 1
 = E 2´ E 2´...´ E 2 – прямое произведение n сомножителей; (x
= E 2´ E 2´...´ E 2 – прямое произведение n сомножителей; (x  ,.., xn)Î
,.., xn)Î  , | E 2| – мощность E 2, | E 2|=2, тогда | Е
, | E 2| – мощность E 2, | E 2|=2, тогда | Е  E 2, причем отображение всюду определено и функционально.
E 2, причем отображение всюду определено и функционально.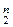 конечно, то задать отображение Е
конечно, то задать отображение Е  ={(0 0),(0 1),(1 0),(1 1)}, отображение Е
={(0 0),(0 1),(1 0),(1 1)}, отображение Е  0.
0. .
. Таблица 2.5
Таблица 2.5 E 2|=4. Для удобства функции пронумерованы так, что двоичный код номера совпадает с набором значений функции.
E 2|=4. Для удобства функции пронумерованы так, что двоичный код номера совпадает с набором значений функции. . Следовательно, число функций двух переменных равно 24=16, занумеруем их числами от 0 до 15 так, чтобы двоичный код номера совпадал с набором значений функции (табл.2.6).
. Следовательно, число функций двух переменных равно 24=16, занумеруем их числами от 0 до 15 так, чтобы двоичный код номера совпадал с набором значений функции (табл.2.6). или вообще его опускают, пишут (х 1 х 2). (х 1& х 2) совпадает с обычным произведением х 1 х 2 и совпадает с min(x 1, x 2). Эту операцию называют также логическим умножением.
или вообще его опускают, пишут (х 1 х 2). (х 1& х 2) совпадает с обычным произведением х 1 х 2 и совпадает с min(x 1, x 2). Эту операцию называют также логическим умножением. x 2), читается «х 1 импликация х 2», иногда обозначается
x 2), читается «х 1 импликация х 2», иногда обозначается  , т. е. х 1 влечет х 2.
, т. е. х 1 влечет х 2. ,&,Ú,
,&,Ú,  .
.


