
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи и упражнения по функциям алгебры логикиСодержание книги
Поиск на нашем сайте
При оперировании с функциями алгебры логики бывают полезны следующие эквивалентности (большинство из них называют обычно основными эквивалентностями алгебры логики). Построив таблицу для соответствующих функций, убедитесь в справедливости следующих эквивалентностей: 1. 2. 3. Дистрибутивность а) б) в) 4. а) 5. а) 6. а) 7. а) в) 8. а) б) 9. а)
1. Построив таблицу для соответствующих функций, убедитесь в справедливости следующих эквивалентностей: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 2. Используя непосредственно определение двойственности булевых функций, а также основные эквивалентности и соотношения, выясните, является ли функция g двойственной к функции f: 1) 2) 3) 4) 5) 6) 7) 8) 9)
Ответы: 4)
3. Используя принцип двойственности, постройте формулу, реализующую функцию, двойственную к функции f, и убедитесь в том, что полученная формула эквивалентна формуле V: 1) 2) 3) 4) 5)
Ответы: 1) 2)
4. Указать все фиктивные переменные у функции f: 1) 2) 3) 4) 5) 6) Ответы: 1) две фиктивные переменные; 3) одна фиктивная переменная; 5) фиктивные переменные x 1 и x 3.
5. Показать, что x 1 – фиктивная переменная у функции f (реализовав для этой цели функцию f формулой, не содержащей явно переменную x 1): 1) 2) 3) 4) 8) Ответы: 4), 8), 10)
6. Представить в СДНФ следующие функции: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) Ответы: 2) 4) 7) 7. Представить в СКНФ следующие функции: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) Ответы: 1)
8. С помощью эквивалентных преобразований построить ДНФ функции 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) Ответы: 4) 10)
9. Используя эквивалентные преобразования, построить КНФ функции 1)
2) 3) 4) 5) 6) 7) Ответы: 1) 3) 6)
10. Применяя преобразования вида 1) 2) 3) 4) 5) 6) 7) 8) Ответы: 2) 5)
11. С помощью преобразований вида 1) 2) 3) 4) 5) 6) 7) 8) Ответы: 1) 5) 12. Используя дистрибутивный закон 1) 2) 3) 4) 5) 6) 7)
Ответы: 3) 6)
13. Используя дистрибутивный закон 1) 2) 3) 4) 5) 6) 7) 8)
Ответы: 2) 5) 14. Методом неопределенных коэффициентов найти полиномы Жегалкина для следующих функций:
Ответы: 1)
15. Методом треугольника Паскаля построить полином Жегалкина для этой функции, если: 1) 3) 5) Ответы: 1)
16. Представив функцию 1) 2) 3) 4) 5) 6) 7) 8)
Ответы: 1) 3)
17. Построить множество всех функций, зависящих от переменных x 1, x 2 и принадлежащих замыканию множества А: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) Ответы: 1)
18. Представив функцию f полиномом, выяснить, является ли она линейной: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) Ответы: 2),3),5),6),8),9)–является. 1),4),7),10)–не является.
19. Выяснить, принадлежит ли функция f множеству T 1\ T 0: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) Ответы: 1),3),4),6),8),9) – является; 2),5),7),10) – не является.
20. По вектору значений 1) 2) 3) 4) 5) 6) 7) 8)
21. Проверить, является ли функция f монотонной: 1) 2) 3) 4) 5) 6) 7) 8) Ответы: 1),2),4),6),7) – является; 3),5),8) – не является.
22. Выяснить, полна ли система функций: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) Ответы: 2),4),6) – полна;1) нет,
23. Выяснить, полна ли система А функций, заданных векторами своих значений: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) Ответы: 3),5) – полна; 1)нет,
24. Выяснить, полна ли система А: 1) 2) 3) 4) 5) 6)
7) 8) 9) 10) Ответы: 1),4),6) – полна; 2)нет,
25. Проверить, является ли система функций А базисом в Р 2: 1) 2) 3) 4) 5) 6) 7) 8) Ответы:1) нет, так как подсистема
26. Из полной в Р 2 системы А выделить всевозможные базисы: 1) 2) 3) 4) 5) 6) 7) 8) Ответы: 1) где 2)
27. Из заданного множества А элементарных конъюнкций выделить простые импликанты функции f: 1) A = 2) A = 3) A = 4) A = 5) A = 6) A =
28. По заданной ДНФ с помощью метода Блейка построить сокращенную ДНФ: 1) 2) 3) 4) 5) 6) 7) 8)
29. Построить сокращенную ДНФ по заданной КНФ: 1) 2) 3) 4) 5) 6) 7) 8)
30. Найти сокращенную ДНФ функции f с помощью минимизирующей карты: 1) 3) 5) 7)
31. С помощью минимизирующих карт построить сокращенную ДНФ для частично определенной функции f, заданной векторно (прочерки соответствуют неопределенным значениям):
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 552; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.18.202 (0.01 с.) |

 – коммутативность связки *, где символ * является общим обозначением для связок &,
– коммутативность связки *, где символ * является общим обозначением для связок &,  ~, |,
~, |,  .
.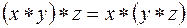 – ассоциативность связки *, где *– общее обозначение для связок &,
– ассоциативность связки *, где *– общее обозначение для связок &,  – дистрибутивность конъюнкции относительно дизъюнкции;
– дистрибутивность конъюнкции относительно дизъюнкции; – дистрибутивность дизъюнкции относительно конъюнкции;
– дистрибутивность дизъюнкции относительно конъюнкции; – дистрибутивность конъюнкции относительно сложения по mod 2.
– дистрибутивность конъюнкции относительно сложения по mod 2. ; б)
; б)  суть правила де Моргана;
суть правила де Моргана; ; б)
; б)  суть правила поглощения;
суть правила поглощения; ; б)
; б)  ;
; ; б)
; б) 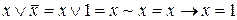 ;
; ; г)
; г)  ; д)
; д) 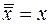 ;
; ;
; ; в)
; в)  ;
; ; б)
; б)  .
. ;
; ;
; ;
;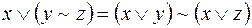 ;
;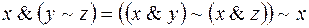 ;
; ;
;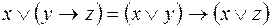 ;
; ;
; ;
; ;
; .
. ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
, 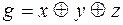 ;
;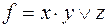 ,
,  ;
; ,
,  ;
; ,
, 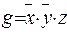 ;
; ,
,  .
. ,
, 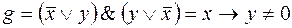 . Значит, g не двойственна к f. 6) – не является; 8),9) – является.
. Значит, g не двойственна к f. 6) – не является; 8),9) – является.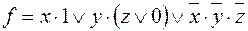 ,
,  ;
;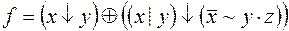 ,
,  ;
;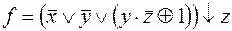 ,
,  ;
;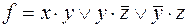 ,
,  ;
; ,
,  .
.
 ; 5)
; 5) 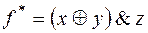 .
.


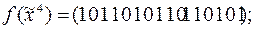
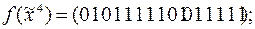
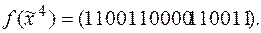
 ;
; ;
; ;
; 5)
5)  6)
6)  7)
7) 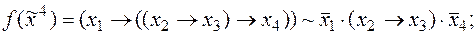
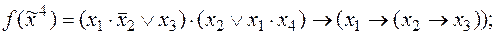 9)
9)  10)
10) 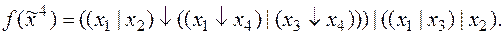
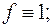 9)
9) 
 ;
;




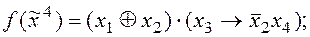
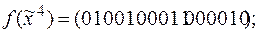

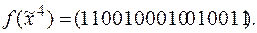
 ;
; ,
,






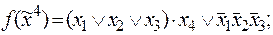



 ; 2)
; 2)  ; 6)
; 6)  ; 8)
; 8) 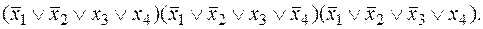
 :
:

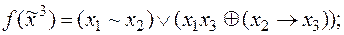




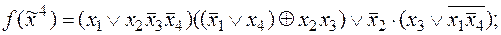
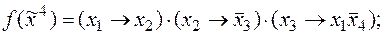



 :
:
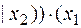


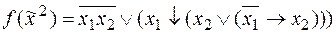 ;
;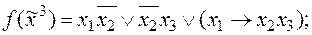

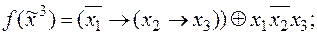



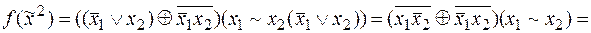



 и
и  построить из заданной ДНФ функции
построить из заданной ДНФ функции  ее совершенную ДНФ:
ее совершенную ДНФ:



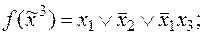


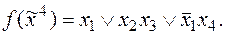


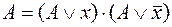 и
и  построить из данной КНФ функции
построить из данной КНФ функции 





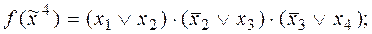



 и эквивалентности
и эквивалентности 

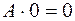 ,
,  и
и  перейти от заданной КНФ функции
перейти от заданной КНФ функции 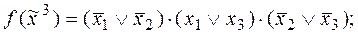




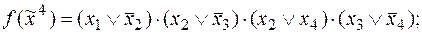

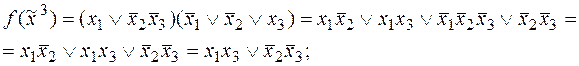

 и эквивалентности
и эквивалентности 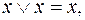

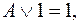
 и
и 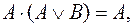 перейти от заданной ДНФ функции
перейти от заданной ДНФ функции  к ее КНФ:
к ее КНФ: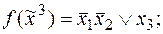




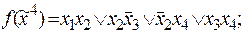










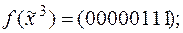

 .
.

 6)
6) 
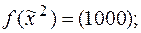 2)
2) 
 4)
4) 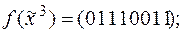
 6)
6) 
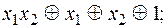 4)
4) 
 }, преобразуйте полученную формулу в полином Жегалкина функции
}, преобразуйте полученную формулу в полином Жегалкина функции 
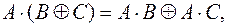

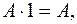

 ):
):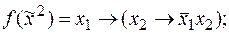


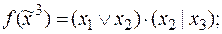








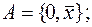












 2)
2)  3)
3)  4)
4)  5)
5)  6)
6) 


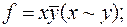




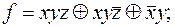
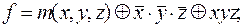



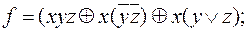

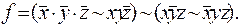


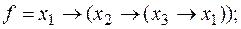



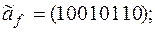



 выяснить, является ли функция f монотонной, самодвойственной и линейной:
выяснить, является ли функция f монотонной, самодвойственной и линейной: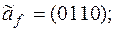






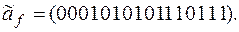
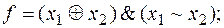

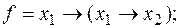

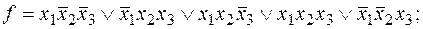








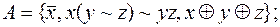




 3) нет,
3) нет,  5)нет,
5)нет, 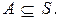




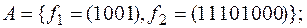
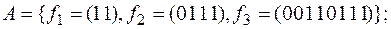




 2)нет,
2)нет, 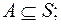 6)нет,
6)нет, 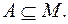




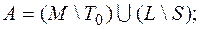





 5)нет,
5)нет, 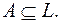





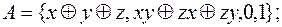


 полна; 2) является; 3) не является,
полна; 2) является; 3) не является,  4)нет, можно удалить
4)нет, можно удалить 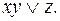



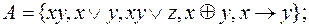
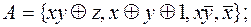
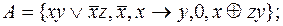
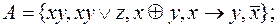




 ,
,  = (00101111);
= (00101111); ,
, 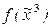 = (01111110);
= (01111110); ,
, 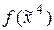 = (1010111001011110);
= (1010111001011110);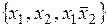 ,
,  = (1011);
= (1011);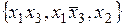 ,
,  ,
, 
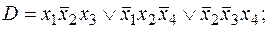




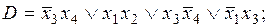









 = (01010111); 2)
= (01010111); 2) 


