Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые свойства элементарных функцийСодержание книги
Поиск на нашем сайте
1. Идемпотентность & и Ú: х & x = x, x Ú x = x. 2. Коммутативность &,Ú,Å,|,~, 3. Ассоциативность &,Ú,Å,~, поэтому в формулах вида xyz можно не ставить никаких скобок. 4. Дистрибутивность: а) & по отношению к Ú: x &(y Ú z)= xy Ú xz, б) Ú по отношению к &: x Ú(y & z)=(x Ú y)&(x Ú z), в) & по отношению к Å: x (y Å z)= xy Å xz. 5. Инволюция: 6. Правила де Моргана: 7. Законы действия с 0 и 1: x Ú0= x, x Ú1=1, x Ú 8. Самодистрибутивность импликации: x Равенство всех этих формул доказывается по определению, т.е. по равенству функций, которые они реализуют. Проверим для примера самодистрибутивность импликации: x
Таблица 2.12
Следствия из свойств элементарных функций 1. Законы склеивания: xy Ú x (x Ú y)&(x 2. Законы поглощения: x Ú xy = x (1Ú y)= x Свойства элементарных функций и теорема о замене подформул на эквивалентные позволяют упрощать формулы.
Пример 2.7 Упростим формулы: 1. x 2 x 3Ú x 1 2. x 1Ú
Принцип двойственности
Определение 2.7. Функция f *(x 1,..., xn) называется двойственной к функции f (x 1,..., xn), если f *(x 1,..., xn) = Пример 2.8. Покажем с помощью таблицы истинности (табл. 2.13) что константа 0 двойственна к 1.
Таблица 2.13
Функции f (x) = x и g (x) = так как f *(0)= Таблица 2.14
Определение 2.8. Если f *(x 1,..., xn) = f (x 1,..., xn), то f (x 1,..., xn) называется самодвойственной. Если f *– самодвойственна, то
Пример 2.9. Покажем, что f (x 1, x 2, x 3)= x 1Å x 2Å x 3 – самодвойственна (табл. 2.15). Таблица 2.15
Пример 2.10. Покажем, что функция х1Úх2 двойственна к x1&x2, функция х1
Таблица 2.16
Теорема 2.1. О двойственных функциях Если f * двойственна к f, то f двойственна к f *. Доказательство. f *(x 1,..., xn) = Предположим, что функция задана формулой. Можно ли найти по этой формуле двойственную функцию? Ответ на этот вопрос дает следующая теорема.
Теорема 2.2. О принципе двойственности Пусть функция h (x 1,..., xn) реализована формулой h (x 1,..., xn) = = g (G 1,..., Gm) = g (f 1(x 1,..., xn),..., fm (x 1,..., xn)), где какие-то переменные могут быть фиктивными. Тогда h *(x 1,..., xn) = g *(f 1*(x 1,..., xn),..., fm *(x 1, …, xn)), это означает, что если функция задана некоторой формулой, то, чтобы получить двойственную функцию, надо в этой формуле все знаки функций заменить на двойственные: 0 на 1, 1 на 0. Доказательство. h *(x 1,..., xn) = (x 1,..., xn)), что и требовалось доказать. Если функция h (x 1,..., xn) реализуется формулой N [ f 1,..., fn ], то формулу, полученную из N заменой fi, входящих в нее, на fi * и реализующую функцию h *(x 1,..., xn), будем называть двойственной и обозначать N *(x 1,..., xn). Пример 2.11. Построить формулу, реализующую f *, если f = =((x Найдем (x Å y)* и (x Таблица 2.17
Из табл. 2.17 видно, что (x По принципу двойственности f *= Тогда f = (f *)* = [ z (x Å y)]* = z Ú(x ~ y).
Разложение булевой функции по переменным Обозначим xs = Посмотрим, чему равно xs при разных значениях x и s (табл. 2.18).
Таблица 2.18
Из табл. 2.18 следует: xs =1 тогда и только тогда, когда x = s.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.157.203 (0.01 с.) |

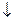 .
.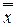 = х.
= х.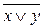 =
= 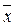 &
& 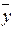 и
и  =
=  .
.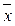 =1, x &0=0, x &1= x, x &
=1, x &0=0, x &1= x, x & 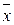 =0, x Å1=
=0, x Å1=  (y
(y 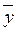 = x (y Ú
= x (y Ú  )= x
)= x 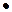 1= x (дистрибутивность & относительно Ú);
1= x (дистрибутивность & относительно Ú); )= x
)= x 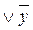 • y = x Ú 0= x (дистрибутивность Ú относительно &).
• y = x Ú 0= x (дистрибутивность Ú относительно &).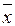 2) = x 3((x 2Ú x 1)&(x 2Ú
2) = x 3((x 2Ú x 1)&(x 2Ú 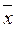 1 x 2Ú
1 x 2Ú  1
1  2 x 3Ú
2 x 3Ú 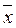 1
1 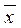 2 x 3 x 4= x 1Ú
2 x 3 x 4= x 1Ú 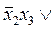
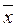 1
1 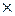
 2
2 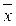 2
2 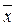 3 х 4)= x 1Ú(x 2Ú x 3)Ú(
3 х 4)= x 1Ú(x 2Ú x 3)Ú(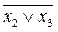 ) x 4= = x 1Ú(x 2Ú х 3Ú(
) x 4= = x 1Ú(x 2Ú х 3Ú(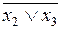 ))(x 2Ú x 3Ú x 4) = x 1Ú x 2Ú x 3Ú x 4.
))(x 2Ú x 3Ú x 4) = x 1Ú x 2Ú x 3Ú x 4.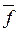 (
(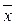 1,...,
1,...,  (1).
(1).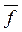 (
(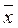 1,...,
1,..., 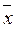 n) = f (x 1,..., xn), т.е. на противоположных наборах функция принимает противоположные значения.
n) = f (x 1,..., xn), т.е. на противоположных наборах функция принимает противоположные значения. (
(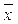 1,...,
1,...,  (
(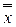 1,...,
1,..., 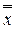 n) = f (x 1,.., xn).
n) = f (x 1,.., xn).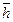 (
( (f 1(
(f 1( (
(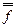 1(
1(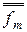 (
(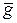 ((
((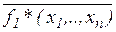 ),..., ((
),..., (( ) = g *(f 1*(x 1,..., xn),..., fm *
) = g *(f 1*(x 1,..., xn),..., fm *
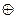 y)*= x ~ y =
y)*= x ~ y = 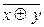 = x
= x  , (x
, (x  y)* =
y)* = 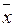 y, x
y, x  y =
y = 
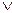 y.
y.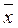 yz
yz 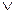 (
(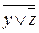 (x
(x 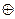 1))=
1))= 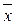 yz
yz 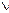
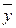 z (x
z (x 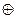 1)= = z (
1)= = z ( y Ú
y Ú 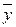 (x Å z Å1))= z (
(x Å z Å1))= z ( ))= = z
))= = z 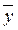 x Å z
x Å z 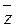 ) = z (
) = z (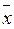 y Ú x
y Ú x 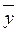 ) = z (x Å y).
) = z (x Å y).