
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема 2.3. О разложении функции по переменнымСодержание книги
Поиск на нашем сайте
f(x1,..., xm, xm+1,..., xn) = где дизъюнкция берется по всем наборам из 0 и 1, которое называется разложением функции f по переменным x 1,..., xn. Прежде чем доказать утверждение, рассмотрим примеры.
Пример 2.12. m = 1, запишем разложение по переменным х: f (x 1,..., xn)=
Пример 2.13. m =2, запишем разложение по переменным х и f (x 1, x 2,… x n) = = = Если f (x 1, x 2) = x 1 Å x 2, то последняя формула дает x 1 Å x 2 =
Доказательство. Для доказательства возьмем произвольный набор (a 1,..., a n) и покажем, что левая и правая части формулы (2.1) принимают на этом наборе одинаковые значения. Слева имеем f (a 1,..., an). Cправа: Дизъюнкция берется по всевозможным наборам (s 1,..., sm). Если в этих наборах хотя бы одно si ¹ ai (1≤ i ≤ m), то
Следствие 2.1. Любую функцию f(x1,..., xn), не равную тождественно нулю, можно представить в виде:
Доказательство. Существование СДНФ для функции, не равной тождественно нулю, вытекает из предыдущей теоремы. Замечание. Cледствие 2.2. Любая функция алгебры логики может быть представлена в виде формулы через отрицание, & и Ú. а) Если f ≡ 0, то f (x 1,..., xn) = б) Если f (x 1,..., xn) ¹ 0 тождественно, тогда ее можно представить в виде СДНФ, где используются только связки
Пример 2.14. Пусть функция f (x 1, x 2, x 3) задана таблицей истинности (2.19). Запишем ее в виде СДНФ. Наборов, на которых функция равна 1, три: (0, 1, 0), (1, 0, 0) и (1, 1, 1), поэтому f (x 1, x 2, x 3) = x 10 & x 21 & x 30 Ú x 11 & x 20 & x 30 Ú x 11& x 21 & x 31 = =
Таблица 2.19
Следствие 2.3. Мы умеем представлять функцию в виде
По принципу двойственности заменим & на Ú и наоборот; получим
Пример 2.15. Пусть f (x 1, x 2, x 3) = x 1 Функция равна нулю только на наборе (1, 1, 0), поэтому f (x 1 x 2 x 3)= x 1
Таблица 2.20
2.5. Полнота, примеры полных систем Определение 2.9. Система функций { f 1, f 2,..., f s,...}Ì P 2 называется полной в Р 2, если любая функция f (x 1,..., xn) Î P 2 может быть записана в виде формулы через функции этой системы.
Полные системы 1. P 2 – полная система. 2. Система M ={ x 1& x 2, x 1Ú x 2,
Пример 2.16. Неполные системы: { Лемма (достаточное условие полноты) Пусть система Доказательство. Пусть h(x1,..., xn) Î P2; так как U полна в Р2, то h(x1,..., xn) =N[f1,..., fs,...] = N[L1[g1,..., gk],..., Ls[g1,..., gk],...] = U[g1,..., gk]. Здесь мы воспользовались тем, что для любого i 3. Система { x 1Ú x 2, Возьмем в качестве полной в Р 2 системы U ={ x 1Ú x 2,
С помощью этой леммы докажем полноту еще ряда систем. 4. Система { x 1& x 2, 5. Система { x 1| x 2} полна в Р 2. Для доказательства возьмем в качестве полной в Р 2 системы U = { x 1& x 2,
6. Система { x 1 7. Система { x 1& x 2, x 1Å x 2, 0, 1}, U = { x 1& x 2, Следствие 2.4. Полином Жегалкина. f (x 1,..., xn) Î P 2, представим ее в виде формулы через конъюнкцию и сумму по модулю два, используя числа 0 и 1. Это можно сделать, так как { x 1& x 2, x 1Å x 2, 0, 1} полна в Р 2. В силу свойства x & & (y Å z)= xy Å xz можно раскрыть все скобки, привести подобные члены, и получится полином от n переменных, состоящий из членов вида х Общий вид полинома Жегалкина
где
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 377; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.46.202 (0.007 с.) |


 ,
,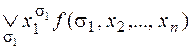 =
= 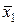 f (0, x 2 , …, xn)Ú x 1 f (1, x 2,..., xn). (2.1)
f (0, x 2 , …, xn)Ú x 1 f (1, x 2,..., xn). (2.1) :
: =
=
 .
.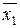 x 2Ú x 1
x 2Ú x 1  .
.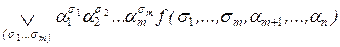 .
.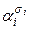 = 0 и
= 0 и  , следовательно, ненулевой член будет только на наборе (s 1,..., sm) = (a 1,..., am), тогда
, следовательно, ненулевой член будет только на наборе (s 1,..., sm) = (a 1,..., am), тогда  =
= 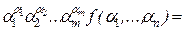 f (a 1,..., an).
f (a 1,..., an).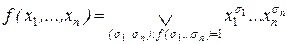 , причём единственным образом. Этот вид называется совершенной дизъюнктивной нормальной формой функции f(x1,..., xn) и записывается СДНФ.
, причём единственным образом. Этот вид называется совершенной дизъюнктивной нормальной формой функции f(x1,..., xn) и записывается СДНФ.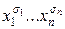 – элементарная конъюнкция ранга n по числу входящих переменных; предполагается, что при i ¹ j, хi ¹ хj. СДНФ для f (x1,..., xn) – дизъюнкция элементарных конъюнкций ранга n. Если функция представлена в виде дизъюнкций элементарных конъюнкций, где ранг хотя бы одной элементарной конъюнкции меньше n, то такая форма называется дизъюнктивной нормальной формой (ДНФ).
– элементарная конъюнкция ранга n по числу входящих переменных; предполагается, что при i ¹ j, хi ¹ хj. СДНФ для f (x1,..., xn) – дизъюнкция элементарных конъюнкций ранга n. Если функция представлена в виде дизъюнкций элементарных конъюнкций, где ранг хотя бы одной элементарной конъюнкции меньше n, то такая форма называется дизъюнктивной нормальной формой (ДНФ).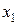 &
& 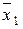 .
. 
 , &, Ú. СДНФ дает алгоритм представления функции в виде формулы через &, Ú,
, &, Ú. СДНФ дает алгоритм представления функции в виде формулы через &, Ú,  .
. Ú x 1&
Ú x 1& 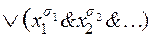 . Нельзя ли представить ее в виде
. Нельзя ли представить ее в виде 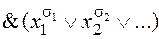 ? Пусть функция f (x1,..., xn) ¹ 1 тождественно. Тогда функция f * ¹ 0 тождественно, и ее можно представить в виде
? Пусть функция f (x1,..., xn) ¹ 1 тождественно. Тогда функция f * ¹ 0 тождественно, и ее можно представить в виде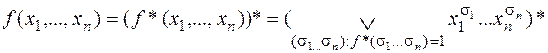
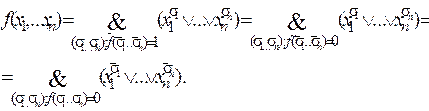 (2.2)
(2.2) называется элементарной дизъюнкцией ранга n. Представление функции в виде (2.2) называется совершенной конъюнктивной нормальной формой или в краткой записи – СКНФ. СКНФ для f (x 1,..., xn) – конъюнкция элементарных дизъюнкций ранга n. КНФ для f (x 1,..., xn) – конъюнкция элементарных дизъюнкций, где ранг хотя бы одной элементарной дизъюнкции меньше n.
называется элементарной дизъюнкцией ранга n. Представление функции в виде (2.2) называется совершенной конъюнктивной нормальной формой или в краткой записи – СКНФ. СКНФ для f (x 1,..., xn) – конъюнкция элементарных дизъюнкций ранга n. КНФ для f (x 1,..., xn) – конъюнкция элементарных дизъюнкций, где ранг хотя бы одной элементарной дизъюнкции меньше n. (x 2
(x 2  Ú x 2
Ú x 2  = x 10Ú x 20Ú x 31=
= x 10Ú x 20Ú x 31=  } – полная система, так как любая функция алгебры логики может быть записана в виде формулы через эти функции.
} – полная система, так как любая функция алгебры логики может быть записана в виде формулы через эти функции. }, {0,1}.
}, {0,1}. U = { f 1, f 2,..., fs,...} полна в Р 2. Пусть B = { g 1, g 2,..., gk,...} – некоторая система из Р 2, причем любая функция fi Î U может быть выражена формулой над B, тогда система B полна в Р 2.
U = { f 1, f 2,..., fs,...} полна в Р 2. Пусть B = { g 1, g 2,..., gk,...} – некоторая система из Р 2, причем любая функция fi Î U может быть выражена формулой над B, тогда система B полна в Р 2. n fi может быть выражена формулой над B, поэтому fi=Li[gi,..., gk].
n fi может быть выражена формулой над B, поэтому fi=Li[gi,..., gk].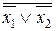 .
. = (x 1| x 2)|(x 1| x 2).
= (x 1| x 2)|(x 1| x 2).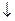 x 2} полна в Р 2. U = { x 1Ú x 2,
x 2} полна в Р 2. U = { x 1Ú x 2, 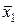 },
},  = (x 1
= (x 1 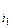 х
х  ... х
... х  , соединенных знаком Å. Такой полином называется полиномом Жегалкина.
, соединенных знаком Å. Такой полином называется полиномом Жегалкина.
 , s = 0, 1,..., n, причем при s = 0 получаем свободный член а 0.
, s = 0, 1,..., n, причем при s = 0 получаем свободный член а 0.


