
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И совершенная конъюнктивная нормальная формаСодержание книги
Поиск на нашем сайте
(КНФ и СКНФ) Определение 1. Элементарной дизъюнкцией п переменных называется дизъюнкция переменных или их отрицаний. Элементарная дизъюнкция п переменных может быть записана в виде:
Определение 2. Конъюнктивной нормальной формой (КНФ) формулы А называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций. Для любой формулы алгебры логики путем равносильных преобразований можно получить ее КНФ, причем не единственную. Например, для формулы
,то есть КНФ А Но так как x А так как Определение 3. КНФ А называется совершенной конъюнктивной нормальной формой формулы А (СКНФ А), если для нее выполнены условия: 1. Все элементарные дизъюнкции, входящие в КНФ А, различны. 2. Все элементарные дизъюнкции, входящие в КНФ А, содержат все переменные. 3. Каждая элементарная дизъюнкция, входящая в КНФ А, не содержит двух одинаковых переменных. 4. Каждая элементарная дизъюнкция, входящая в КНФ А, не содержит переменную и ее отрицание. Можно доказать, что каждая не тождественно истинная формула имеет единственную СКНФ. Один из способов получения СКНФ состоит в использовании таблицы истинности для формулы А. Действительно, получив с помощью таблицы истинности СДНФ А, мы получим СКНФ А, взяв отрицание Другой способ получения СКНФ, использующий равносильные преобразования, состоит в следующем: 1. Путем равносильных преобразований формулы А получают одну из КНФ А. 2. Если в полученной КНФ А входящая в нее элементарная дизъюнкция В не содержит переменную xi, то, используя равносильность 3. Если в КНФ А входят две одинаковых элементарных дизъюнкции В, то лишнюю можно отбросить, пользуясь равносильностью В&В 4. Если некоторая элементарная дизъюнкция, входящая в КНФ А, содержит переменную хi дважды, то лишнюю можно отбросить, пользуясь равносильностью 5. Если некоторая элементарная дизъюнкция, входящая в КНФ А, содержит переменную хi и ее отрицание, то
Ясно, что после описанной процедуры будет получена СКНФ А. Например, для формулы Так как обе элементарные дизъюнкции различны и содержат все переменные (х и у), то первое и второе условия СКНФ А выполнены. Элементарная дизъюнкция § 12. Проблема разрешимости Все формулы алгебры логики делятся на три класса: 1) тождественно истинные, 2) тождественно ложные и 3) выполнимые. Определения тождественно истинной и тождественно ложной формул даны выше. Формулу А называют выполнимой, если она принимает значение «истина» хотя бы на одном наборе значений входящих в нее переменных и не является тождественно истинной. В связи с этим возникает задача: к какому классу относится данная формула? Эта задача носит название проблемы разрешимости. Очевидно, проблема разрешимости алгебры логики разрешима. Действительно, для каждой формулы алгебры логики может быть записана таблица истинности, которая и даст ответ на поставленный вопрос. Однако практическое использование таблицы истинности для формулы А(х1,х2,...,хп) при больших п затруднительно. Существует другой способ, позволяющий, не используя таблицы истинности, определить, к какому классу относится формула А. Этот способ основан на приведении формулы к нормальной форме (КНФ или ДНФ) и использовании алгоритма, который позволяет определить, является ли данная формула тождественно истинной или не является. Одновременно с этим решается вопрос о том, будет ли формула А выполнимой. Предположим, что мы имеем критерий тождественной истинности для формул алгебры логики. Рассмотрим механизм его применения. Применим критерий тождественной истинности к формуле А. Если окажется, что формула А - тождественно истинная, то задача решена. Если же окажется, что формула А не тождественно истинная, то применим критерий тождественной истинности к формуле Если же формула
Установим теперь критерий тождественной истинности произвольной формулы алгебры логики. С этой целью предварительно сформулируем и докажем критерий тождественной истинности элементарной дизъюнкции. Теорема 1. Для того, чтобы элементарная дизъюнкция была тождественно истинной, необходимо и достаточно, чтобы в ней содержалась переменная и ее отрицание. Доказательство. Необходимость. Пусть элементарная дизъюнкция тождественно истинна, но в нее одновременно не входит некоторая переменная и ее отрицание. Придадим каждой переменной, входящей в элементарную дизъюнкцию без знака отрицания, значение ложь, а каждой переменной, входящей в элементарную дизъюнкцию под знаком отрицания - значение «истина». Тогда, очевидно, вся элементарная дизъюнкция примет значение ложь, что противоречит условию. Достаточность. Пусть теперь элементарная дизъюнкция содержит переменную и ее отрицание. Так как Критерий тождественной истинности элементарной дизъюнкции позволяет сформулировать и доказать критерии тождественной истинности произвольной формулы алгебры логики. Теорема 2. Для того, чтобы формула алгебры логики А была тождественно истинна, необходимо и достаточно, чтобы любая элементарная дизъюнкция, входящая в КНФ А, содержала переменную и ее отрицание. Доказательство. Необходимость. Пусть А - тождественно истинна. Тогда и КНФ А - тождественно истинна. Но КНФ А Достаточность. Пусть любая элементарная дизъюнкция Ai, входящая в КНФ А, содержит переменную и ее отрицание. Тогда по теореме 1 Например, выясним, является ли формула Так как Аналогично можно установить критерий тождественной ложности формулы алгебры логики, используя ее ДНФ. Теорема 3. Для того, чтобы элементарная конъюнкция была тождественно ложной, необходимо и достаточно, чтобы в ней содержалась переменная и ее отрицание. Теорема 4. Для того, чтобы формула алгебры логики А была тождественно ложной, необходимо и достаточно, чтобы любая конъюнкция, входящая в ДНФ А, содержала переменную и ее отрицание.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1156; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.55.1 (0.01 с.) |

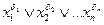 ,
,
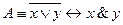 имеем:
имеем: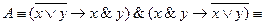
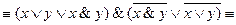

 ,
, 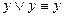 ,
, 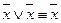 ,
, 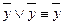 , то KHФ
, то KHФ 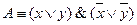
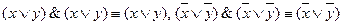 , то КНФ
, то КНФ  .
.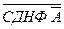 , то есть СКНФ
, то есть СКНФ  .
. , элементарную дизъюнкцию В заменяют на две элементарные дизъюнкции
, элементарную дизъюнкцию В заменяют на две элементарные дизъюнкции 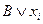 и
и 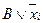 каждая из которых содержит переменную xi.
каждая из которых содержит переменную xi. В.
В.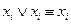 .
.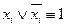 и, следовательно, вся элементарная дизъюнкция имеет значение 1, а поэтому ее можно отбросить, как единичный член конъюнкции.
и, следовательно, вся элементарная дизъюнкция имеет значение 1, а поэтому ее можно отбросить, как единичный член конъюнкции.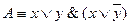 КНФ
КНФ 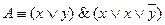 .
.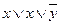 содержит переменную х дважды, но
содержит переменную х дважды, но 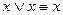 , и поэтому КНФ
, и поэтому КНФ 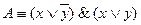 ; причем ни одна из элементарных дизъюнкций не содержит переменную и ее отрицание. Значит, теперь выполнены все условия СКНФ А, и, следовательно, СКНФ
; причем ни одна из элементарных дизъюнкций не содержит переменную и ее отрицание. Значит, теперь выполнены все условия СКНФ А, и, следовательно, СКНФ 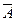 . Если окажется, что формула А - тождественно истинная, то ясно, что формула
. Если окажется, что формула А - тождественно истинная, то ясно, что формула 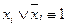 , то и вся элементарная дизъюнкция будет тождественно истинной.
, то и вся элементарная дизъюнкция будет тождественно истинной.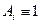 (i = 1,2..... n). При этом и КНФ
(i = 1,2..... n). При этом и КНФ  .
.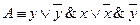 тождественно истинной.
тождественно истинной. , то ясно, что каждая элементарная дизъюнкция
, то ясно, что каждая элементарная дизъюнкция 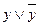 и
и 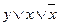 , входящая в КНФ А, содержит переменную и ее отрицание. Следовательно, A
, входящая в КНФ А, содержит переменную и ее отрицание. Следовательно, A 


