
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебра Жегалкина. Основные свойства операций алгебры Жегалкина.Содержание книги
Поиск на нашем сайте
Определение. Алгеброй Жегалкина называется алгебра над множеством логических функций и переменных, сигнатура которой содержит две бинарные операции & и В алгебре Жегалкина выполняются следующие соотношения: 1. x 2. x (y 3. x 4. x 5. x Эти соотношения легко проверить табличным способом. Кроме перечисленных соотношений в алгебре Жегалкина выполняются соотношения булевой алгебры относительно конъюнкции и констант. Функцию Шеффера, функцию стрелка Пирса и можно представить следующими эквивалентными формулами: х1 / x2 =
Найдем выражения для основных элементарных функций алгебры логики в алгебре Жегалкина. 1. Это соотношение проверяется непосредственной подстановкой 0 и 1 в обе части равенства. 2. x Доказательство: x = x y 3. x ’ y = x y Доказательство: Используем выражение для импликсации в. Тогда: x ’ y = = x y 4. x / y = x y Доказательство: Используем выражение для x / y. Тогда: x / y = 5. x “ y = x y Доказательство: Используем выражение для x “ y. Тогда: x “ y = 6. x ~ y = 1 Доказательство: Легко проверить, что x ~ y = x y x ~ y = x y 29. Алгебра Жегалкина. Представление логических функций полиномом Жегалкина.
Определение. Полиномом Жегалкина для n логических переменных называется полином, являющийся суммой константы и различных одночленов, в которые все переменные входят не выше, чем в первой степени: a причем в каждом наборе (i Например, 1 От формулы алгебры логики всегда можно перейти к формуле алгебры Жегалкина. Для этого нужно заменить основные элементарные функции алгебры логики на соответствующие эквивалентные выражения алгебры Жегалкина (1) - (5), представленные выше. В полученной формуле нужно раскрыть скобки и произвести упрощения, используя соотношения (1.4), а также следующие соотношения: x & x = x и x·1 = x. Полученное выражение и будет полиномом Жегалкина для данной формулы. Пример. Найти полином Жегалкина для функции: f(x, y) = (x
Полученное выражение и есть полином Жегалкина. При нахождении полинома Жегалкина для некоторой формулы алгебры логики можно использовать следующее соотношение, вытекающее из представления дизъюнкции в алгебре Жегалкина: f1 справедливое при f1f2 = 0. Используем соотношение (1.5) для нахождения полинома Жегалкина в следующих примерах. Пример. Найти полином Жегалкина для функции: f(x, y) = x y Сделаем следующие преобразования: f(x,y) = x y = x y Пример. Найти полином Жегалкина для функции: f(x, y) = x Сделаем следующие преобразования: f(x,y) = x = x y Теорема. Для любой логической функции существует полином Жегалкина и притом единственный. Доказательство: Существование полинома доказано вышеприведенным алгоритмом получения полинома из логической формулы. Для доказательства единственности надо показать, что между множеством всех логических функций от n переменных и множеством всех полиномов Жегалкина от n переменных существует взаимно однозначное соответствие. Полином Жегалкина можно найти методом неопределенных коэффициентов. Рассмотрим этот метод на следующим примере. Пример. Найти полином Жегалкина для функции заданной векторно: f(x,y) = (0, 1, 1, 0). Составим таблицу 1.14 задания данной функции. Таблица 1.14
Полином Жегалкина для функции двух переменных ищем в следующем виде: f(x, y) = a0 Для определения коэффициентов полинома нужно подставить значения неизвестных и соответствующее значение функции в (1.6), согласно таблице 1.14. Подставляя набор переменных(0,0) в (1.6) получим:
Аналогично для набора (0,1) получим: Для набора (1,0) получим: Для набора (1,1) получим: Подставляя в (1.6) найденные значения коэффициентов получим искомый полином для данной функции: f(x, y) = x Замечание. Можно показать, что переменная x
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 2830; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.46.87 (0.008 с.) |

 , и две нульарные операции – константы 0 и 1.
, и две нульарные операции – константы 0 и 1. = 1;
= 1;
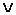
 =
=  , x1 “ x2 =
, x1 “ x2 =  &
&  =
= 
 =
= 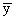
 = xy
= xy  x
x 
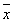
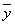 . Тогда:
. Тогда: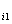 x
x  … x
… x  , (1 d k d n)
, (1 d k d n) ,, i
,, i  ) все i
) все i 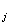 различны, а суммирование по mod 2 ведется по некоторому множеству таких не совпадающих наборов.
различны, а суммирование по mod 2 ведется по некоторому множеству таких не совпадающих наборов. , x
, x 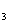


 .
. = x y
= x y 
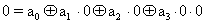 .
.  a
a  = 0.
= 0. .
. 

 будет фиктивной для некоторой функции тогда и только тогда, когда полином Жегалкина для нее не содержит переменной x
будет фиктивной для некоторой функции тогда и только тогда, когда полином Жегалкина для нее не содержит переменной x 


