
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о числе подмножеств n-элементного множества.Содержание книги
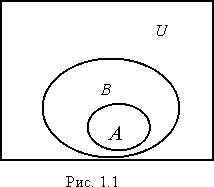
Поиск на нашем сайте Основные понятия теории множеств. Понятие множества — является одним из тех фундаментальных понятий математики, которым трудно дать точное определение, используя элементарные понятия. Поэтому ограничимся описательным объяснением понятия множества. Множеством называется совокупность определенных вполне различаемых объектов, рассматриваемых как единое целое. Создатель теории множеств Георг Кантор давал следующее определение множества — «множество есть многое, мыслимое нами как целое». Отдельные объекты, из которых состоит множество, называются элементами множества. Множества принято обозначать большими буквами латинского алфавита, а элементы этих множеств — маленькими буквами латинского алфавита. Множества записываются в фигурных скобках { }. Принято использовать следующие обозначения: a ∈ X — «элемент a принадлежит множеству X»; a ∉ X — «элемент a не принадлежит множеству X»; ∀ — квантор произвольности, общности, обозначающий «любой», «какой бы не был», «для всех»; ∃ — квантор существования: ∃y ∈ B — «существует (найдется) элемент y из множества B»; ∃! — квантор существования и единственности: ∃!b ∈ C — «существует единственный элемент b из множества C»; : — «такой, что; обладающий свойством»; → — символ следствия, означает «влечет за собой»; ⇔ — квантор эквивалентности, равносильности — «тогда и только тогда». Множества бывают конечные и бесконечные. Множества называются конечным, если число его элементов конечно, т.е. если существует натуральное число n, являющееся числом элементов множества. А={a1, a2,a 3,..., an}. Множество называется бесконечным, если оно содержит бесконечное число элементов. B={b1,b2,b3,...}. Например, множество букв русского алфавита — конечное множество. Множество натуральных чисел — бесконечное множество. Число элементов в конечном множестве M называется мощностью множества M и обозначается |M|. Пустоемножество — множество, не содержащее ни одного элемента — ∅. Два множества называются равными, если они состоят из одних и тех же элементов, т.е. представляют собой одно и тоже множество. Множества не равны X ≠ Y, если в Х есть элементы, не принадлежащие Y, или в Y есть элементы, не принадлежащие Х. Символ равенства множеств обладает свойствами: Х=Х; — рефлексивность если Х=Y, Y=X — симметричность если X=Y,Y=Z, то X=Z — транзитивность. Согласно такого определения равенства множеств мы естественно получаем, что все пустые множества равны между собой или что то же самое, что существует только одно пустое множество. Понятие мультимножества. Мультимножество — в математике, обобщение понятия множества, допускающее включение одного и того же элемента по нескольку раз Число элементов в мультимножестве, с учетом повторяющихся элементов, называется его размером или мощностью. Способы задания множеств. Множество может быть задано перечислением всех его элементов или списком. В этом случае элементы множества записывают внутри фигурных скобок, например: А = { 1, 2, a, x } или B = { река Нил, город Москва, планета Уран}. Множество может быть задано описанием свойств его элементов. Чаще всего при этом используют запись A = { x|P(x) }, которую читают следующим образом: "A есть множество элементов x таких, что для них выполняется свойство P(x)". Например, B = { x| x- натуральное число, меньшее 10 }, при этом, очевидно, B = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }. Множество можно задать порождающей процедурой, например: D = { z|1 О D,и если z О D,то z + 3 О D}, E = { x| x = 3k, k - любое нартуральное число.} Наряду с порождающей процедурой существует распознающая или разрешающая процедура, которая позволяет определить, принадлежит ли данный объект множеству или нет. Для множества D распознающая процедура заключается в том, что для любого натурального числа n будут проверять, является ли число 3 делителем числа n - 1. Для множества E распознающая процедура заключается в разложении числа на простые множители. Операции над множествами. Множество A называется подмножеством множества B, если любой элемент множества A принадлежит множеству B. При этом пишут A М B, где " М " есть знак вложения подмножества. Из определения следует, что для любого множества A справедливы, как минимум, два вложения A М A и A М U. В теории множеств, по определению, полагают, что пустое множество является подмножеством любого множества. Пустое множество и само множество A называются несобственными подмножествами множества A. При графическом изображении множеств удобно использовать диаграммы Венна, на которых универсальное множество обычно представляют в виде прямоугольника, а остальные множества в виде овалов, заключенных внутри этого прямоугольника (рис 1.1).
Объединением множеств A и B (обозначение A A
Пересечением множеств A и B (обозначение A A
Разностью множеств A и B называется множество всех тех элементов множества A, которые не принадлежат множеству B (рис. 1.4): A\B = {x|x
Симметрической разностью множеств A и B называется множество A
Абсолютным дополнением множества A называется множество всех элементов, не принадлежащих A, т.е. множество `A = U\A={x|x
Задание отображений. Для задания (записи) отображений используются следующие основные способы: Аналитический способ – в виде формулы. Табличный способ. В первой строчке таблицы записываются элементы (числа) области определения, во второй – элементы множества значений. Графический способ – на координатной плоскости. С помощью графов - двух кругов или иных геометрических фигур и стрелок. Словесный способ – в виде текста, описывающего закон соответствия Виды отображений. Отображения делятся на два вида: отображения “в” и “на”. Пусть задано отображение B=f (A) 1. Отображение “в” – инъекция. Соответствие, при котором каждому элементу множества A соответствует единственный элемент множества B, а каждому элементу множества B соответствует не более одного прообраза из A. При этом, мощность множества A меньше мощности множества B. 2. Отображение “на” – сюръекция. Соответствие, при котором каждому элементу множества A соответствует единственный элемент множества B, а каждому элементу множества B соответствует хотя бы один прообраз из A. При этом, мощность множества A больше или равна мощности множества B. Особое место занимают взаимнооднозначные отображения (соответствия). Взаимнооднозначное отображение (соответствие) – биекция. Соответствие, при котором каждому элементу множества A соответствует единственный элемент множества B и каждому элементу множества B соответствует один прообраз из множества A. При этом мощность множества A равна мощности множества B. Множества будут равномощными (равносильными, эквивалентными), если между ними можно установить (задать) взаимнооднозначное соответствие. Для взаимнооднозначных отображений, обратное отображение также является взаимнооднозначным отображением.
Определение кольца Кольцом
Пример 5.8.Все целые положительные и отрицательные числа и нуль образуют коммутативное кольцо с единицей относительно обычных операций сложения и умножения. Пример 5.9.Легко убедиться, что полная система вычетов по модулю Кольцо вычетов по модулю При описании блочных кодов [25, 30, 33] широко используется понятие кольца вычетов по модулю некоторого полинома Для полиномов существуют понятия, аналогичные введенным в 5.8 для чисел, если заменить в этих понятиях слово «число» словом «полином». Так, если при делении полиномов Все полиномы, сравнимые между собой по модулю Совокупность классов вычетов по модулю Пример 5.13.Рассмотрим кольцо классов вычетов по модулю полинома
Здесь 10. Определение поля Полем Другими словами, полем называют множество, которое является аддитивной абелевой группой; ненулевые же элементы этого множества образуют мультипликативную абелевую группу, и выполняется закон дистрибутивности. По аналогии с группами число элементов поля называется порядком поля. Поля, порядки которых конечны, называются конечными полями. Конечные поля имеют наибольшее значение в теории кодирования. Отметим некоторые свойства полей, вытекающие из их определения. 1. Для любого элемента поля 2. Для ненулевых элементов 3. Для любых элементов 4. Если Пример 5.10Множество всех действительных чисел образует поле. Существует также поле комплексных чисел, поле рациональных чисел, но не может быть поля целых чисел, поскольку обратные элементы по умножению, кроме единицы, не являлись бы целыми. Пример 5.11. Множество чисел Пример 5.12.При
Перестановки Перестановки. Перестановкой называется расположение элементов множества в определенном порядке. Теорема. Число перестановок n -элементного множества S, т.е. число способов его упорядочивания выражается формулой Pn=n!. Символом n! обозначается произведение натуральных чисел от 1 до n: n!=1×2×...× n. Считается, что 0!=1. Доказательство. Будем последовательно выбирать элементы множества S и располагать их в определенном порядке на n местах. На первое место можно поставить любой из n элементов. После того, как заполнено первое место, на второе место можно поставить любой из оставшихся n -1 элементов и т.д. Тогда по правилу произведения все n мест можно заполнить n ×(п -1)×(п -2)×...×2×1= n! способами. Следовательно, n -элементное множество можно упорядочить n! способами.
Перестановки с повторениями Перестановки с повторениями. Перестановкой с повторениями называется расположение элементов мультимножества в определенном порядке. Теорема. Число перестановок с повторениями для мультимножества где Доказательство 1. Рассмотрим одну перестановку мультимножества и заменим в ней все одинаковые элементы разными. Тогда, число различных перестановок, которые можно составить из рассматриваемой перестановки, равно k 1!× k 2!×…× km!. Проделав это для каждой перестановки, получим n! перестановок. Следовательно, Cn (k 1, k 2,…, km)× k 1!× k 2!×…× km!= n!, Число Cn (k 1, k 2,…, km) называется полиномиальным коэффициентом. Приведем еще одно доказательство данной теоремы. Доказательство 2. Для упорядочивания мультимножества необходимо из n мест выбрать k 1 мест для элемента s 1, что можно сделать
13. Понятие сочетания. Теорема о числе сочетаний из n элементов по k. Свойства сочетаний. Сочетанием из n элементов по m (иногда читают просто: из n по m) называется m-элементное подмножество некоторого n-элементного множества. Теорема. Число сочетаний из n элементов по k определяется по формуле:
Свойства сочетаний
Первое свойство непосредственно вытекает из формул:
Доказательство: Составим 1-й класс - сочетания, содержащие элемент 2-й класс - сочетания, не содержащие элемент Если из любого сочетания 1-го класса откинуть элемент Сочетания 2-го класса являются
Доказательство:
Сильная связность. Отношение Пусть
Пример ориентированного графа с тремя компонентами сильной связности. Ориентированный граф Граф сильно связен, если для любых вершин х у существует путь, идущий из х в у.
26. Понятие логической функции. Способы задания логических функций. Логическая функция - это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1. Способы задания функций алгебры логики АЛ Логической функцией называется зависимость поведения выходных логических величин от изменения входных логических величин. Задачей алгебры логики является поиск математического или функционального представления логических функций с целью ее непосредственного использования для управления объектом или процессом. Имеются различные способы представления логических взаимодействий. Табличный способ. При этом способе функция задается в виде таблицы истинности, представляющей собой совокупность всех комбинацийвходных переменных (левые столбцы) и соответствующих им значений функции (правый столбец). Таблица истинности содержит 2n строк, n +m столбцов (количество входов n +количество выходов m). Например: пусть требуется задать функцию двух переменных, т.е. дискретное устройство на два входа и на один выход, следовательно, число столбцов = 2+1, а число строк = 4.
Таблица. 3.2Пример таблицы истинности Таблицы истинности возможно составить по условиям задания. Задание на управление для выше приведенного примера может выглядеть следующим образом: лампа А горит только тогда, когда одновременно нажаты обе кнопки x и y. Таблицы истинности позволяют автоматизировать поиск искомой логической функции в математическом виде. Словесно-аналитический способ задания функции алгебры логики. При этом способе функция задается в виде аналитического выражения.В левой части высказывания указывается действие управляемого привода (или исполнительного устройства), а в правой части- условие, при котором выполняется это действие. Аналитическое выражение задается в возможно более краткой форме. Некоторые подразумеваемые слова могут опускаться, например, такие как «кнопка», «нажать», «активен» и другие. Название датчиков и кнопок возможно заменять их схемным обозначением. При этом указание на датчик означает то, что этот датчик изменил свое состояние на активное (логическая 1). Ударение делается на союзы предложения, которые, в большинстве случаев, указывают на логическое действие.
В данном примере описана работа распределителя, с помощью которого производиться управление цилиндром.Электромагнит Y1 включиться (соответственно цилиндр начнет свое движение), если будет нажата кнопка S1 и датчикB1 активен. Союз и указывает на логическое взаимодействие сигналов управления от кнопки и датчика. Для поиска несложных логических функций аналитический способ является наиболее простым и быстрым. Однако, этот способ в большей степени основан на интуиции. Поэтому для поиска сложных функций он не используется. Графические способы. Для графического описания логических взаимодействий можно использовать разные способы, предлагаемые стандартом IEC 848: шаговая, временная диаграмма, логические функциональные схемы, функциональный план. При взаимодействии нескольких приводов наиболее наглядным средством установления логических взаимосвязей является шаговая диаграмма. Рис. 3.4 Пример шаговой диаграммы В шаговой диаграмме различают линии состояния или положения привода (в данном случае это линия, описывающая перемещение цилиндра) и линии управляющих сигналов. Отличием от временной диаграммы является то, вместо временной оси здесь использованы шаги- условные временные отрезки. Длина шага не пропорциональна реальному времени, а связанна с одним действием управляемого объекта. Сигналы взаимодействуют друг с другом (сливание потоков информации) по определенному логическому закону. Каждое логическое действие имеет собственное обозначение. Достоинством шаговой диаграммы является наглядность связей взаимодействия приводов и сигналов управления между собой во времени.
Рис. 3.5 Пример временной диаграммы Из диаграммы следует, что лампа Н1 «горит» тогда, когда нажата кнопка S1 и не нажата кнопка S2. Лампа Н2 «горит» тогда, когда нажата кнопка S2 и не нажата кнопка S1. Логические функциональные блок-схемы состоят из логически связанных между собой отдельных функциональных блоков, которые являются обозначениями элементарных логических функций.
Логические функциональные блок-схемы обладают всеми достоинствами графического изображения- это наглядность связей логических функциональных блоков. Недостатком данных схем является сложность прослеживания изменения сигналов во времени. Логические функциональные блок-схемы являются одним из самых распространенных языков программирования в промышленности. Напомним, что целью алгебры логики является получение математического или функционального изображения функции. Функциональный план является графическим средством отображения по-шагового управления процессом. Весь процесс управления разбит на отдельные шаги (минимальные части процесса управления), которые осуществляются при выполнении определенных условий. Функциональный план является языком программиров Рис. 3.6 Пример функционального плана Математическое представление алгебры логики. Элементарные логические действия можно представить с помощью специальных или арифметических символов (AND: , ·;OR: , +; NO:a`), обозначающих логические действия. Используя законы алгебры логики, возможны преобразования математических выражений логических функций.
Булеву функцию можно задать с помощью единичного п – мерного куба (рис. 7).
Рис. 7 Единичным п – мерным кубом называется граф, каждая вершина которого взаимно однозначно соответствует двоичному набору. Две вершины соединены ребром, если соответствующие наборы отличаются только в одном разряде (в одной координате). На рис. 7 показаны п- мерные кубы для булевых функций: двух переменных (а), трех переменных (б), четырех переменных (в). Отметив вершины, в которых булева функция принимает единичные значения, получим геометрическое представление булевой функции. Так функция примет вид:
Часто для изображения булевых функций двух и трех переменных используют прямоугольную систему координат:
Рис. 9 Изображение булевых функций числа переменных более трех в этом случае невозможен. В методе минимизации булевых функций Квайна – Мак- Класки используется кубическое представление булевых функций (аналог п- мерных кубов). Терм максимального ранга принято называть 0-кубом и обозначать К 0. Если два 0-куба из комплекса К 0 различаются только по одной координате, то они образуют куб (отрезок) K 1. 27. Булева алгебра. Основные свойства операций булевой алгебры. Понятие двойственной и самодвойственной логической функции. Булевой алгеброй называется непустое множество A с двумя бинарными операциями
Некоторые свойства Из аксиом видно, что наименьшим элементом является 0, наибольшим является 1, а дополнение a любого элемента a однозначно определено. Для всех a и b из A верны также следующие равенства:
Основные тождества В данном разделе повторяются свойства и аксиомы, описанные выше с добавлением ещё нескольких. Сводная таблица свойств и аксиом, описанных выше:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 2564; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.013 с.) |

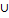 B) называется множество элементов x таких, что x принадлежит хотя бы одному из двух множеств A или B (рис 1.2). Символически это можно записать следующим образом:
B) называется множество элементов x таких, что x принадлежит хотя бы одному из двух множеств A или B (рис 1.2). Символически это можно записать следующим образом: A или x
A или x 
 B) называется множество, состоящее из элементов x, которые принадлежат и множеству A и множеству B (рис. 1.3):
B) называется множество, состоящее из элементов x, которые принадлежат и множеству A и множеству B (рис. 1.3): A и x
A и x 

 B = (A\B)
B = (A\B) 

 называется множество элементов, на котором определены две операции – сложение и умножение, и в
называется множество элементов, на котором определены две операции – сложение и умножение, и в 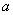 и
и  из
из  (замкнутость операции умножения).
(замкнутость операции умножения).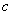 из
из  и
и  .
. и
и  .
. также образует коммутативное кольцо с единицей относительно операций сложения и умножения по модулю
также образует коммутативное кольцо с единицей относительно операций сложения и умножения по модулю  .
.
 .
.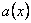 и
и  из
из  на
на 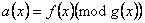 .
. над двоичным полем. Полиномы вида
над двоичным полем. Полиномы вида 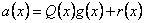 , где
, где  – произвольный полином, степень которого меньше 2, при фиксированном
– произвольный полином, степень которого меньше 2, при фиксированном 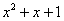 . Так как всего имеется 4 разных полинома
. Так как всего имеется 4 разных полинома 


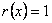





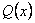 – произвольный полином. В качестве представителей классов обычно выбирают вычеты наименьшей степени, которые совпадают с полиномами
– произвольный полином. В качестве представителей классов обычно выбирают вычеты наименьшей степени, которые совпадают с полиномами  .
. .
. .
. .
. и
и  , то
, то  .
. , где
, где  имеем простейшее двоичное поле, состоящее из двух элементов 0 и 1. Эти элементы являются соответственно единичными элементами относительно операций сложения и умножения по модулю 2, которые определяются правилами:
имеем простейшее двоичное поле, состоящее из двух элементов 0 и 1. Эти элементы являются соответственно единичными элементами относительно операций сложения и умножения по модулю 2, которые определяются правилами:  ;
; 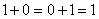 ;
;  ;
;  ;
;  . Так как
. Так как  , то операции сложения и вычитания в двоичном поле совпадают, а так как
, то операции сложения и вычитания в двоичном поле совпадают, а так как  , также совпадают операции умножения и деления. Это поле находит широкое применение в теории и технике помехоустойчивого кодирования.
, также совпадают операции умножения и деления. Это поле находит широкое применение в теории и технике помехоустойчивого кодирования. выражается формулой
выражается формулой ,
, .
.
 способами, затем из n - k 1оставшиеся мест выбрать k 2 мест для элемента s 2, что можно сделать
способами, затем из n - k 1оставшиеся мест выбрать k 2 мест для элемента s 2, что можно сделать  способами и т.д. Тогда число способов упорядочивания мультимножества S по правилу произведения равно (напомнив, что 0!=1)
способами и т.д. Тогда число способов упорядочивания мультимножества S по правилу произведения равно (напомнив, что 0!=1)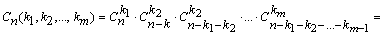
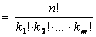 .
.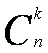 =
=  .
.
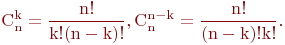
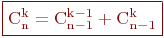
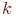 -элементные сочетания из
-элементные сочетания из  элементов
элементов  и разобьем их на два класса:
и разобьем их на два класса: ;
; сочетание из
сочетание из  , их число
, их число  .
. . Поскольку любое
. Поскольку любое  принадлежит одному и только одному из этих классов, а общее число равно
принадлежит одному и только одному из этих классов, а общее число равно  , то приходим к равенству
, то приходим к равенству
 - это число всех
- это число всех  элементов 2-го типа. Размещения k-го класса - это не что иное, как всевозможные перестановки из
элементов 2-го типа. Размещения k-го класса - это не что иное, как всевозможные перестановки из 
 на вершинах графа называется отношением сильной связности. Сильная связность — отношение эквивалентности. Рассмотрим транзитивность:
на вершинах графа называется отношением сильной связности. Сильная связность — отношение эквивалентности. Рассмотрим транзитивность: 
 — ориентированный граф. Компонентой сильной связности называется класс эквивалентности множества вершин этого графа относительно сильной связности.
— ориентированный граф. Компонентой сильной связности называется класс эквивалентности множества вершин этого графа относительно сильной связности.
 Рис. 3.3 Пример аналитического задания логической функции
Рис. 3.3 Пример аналитического задания логической функции
 Временные диаграммы важны для изображения динамически изменяющихся процессов. Горизонтальная ось является временной. Временные диаграммы удобны для изображения динамических процессов, которые быстро изменяются во времени. Они позволяют визуально анализировать реакцию выходных величин на изменение входных.
Временные диаграммы важны для изображения динамически изменяющихся процессов. Горизонтальная ось является временной. Временные диаграммы удобны для изображения динамических процессов, которые быстро изменяются во времени. Они позволяют визуально анализировать реакцию выходных величин на изменение входных. Рис. 3.5 Пример логической функциональной блок-схемы
Рис. 3.5 Пример логической функциональной блок-схемы ания.
ания.

 Рис. 8
Рис. 8
 (аналог конъюнкции),
(аналог конъюнкции),  (аналог дизъюнкции), унарной операцией
(аналог дизъюнкции), унарной операцией  (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:
(аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:









 ;
;
 ;
;
 ;
;
 ;
;
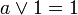 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
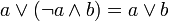 ;
;
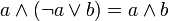 .
.



