
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие сильной связности. Анализ сильной связности с помощью алгоритмов поиска на графах.Содержание книги
Поиск на нашем сайте
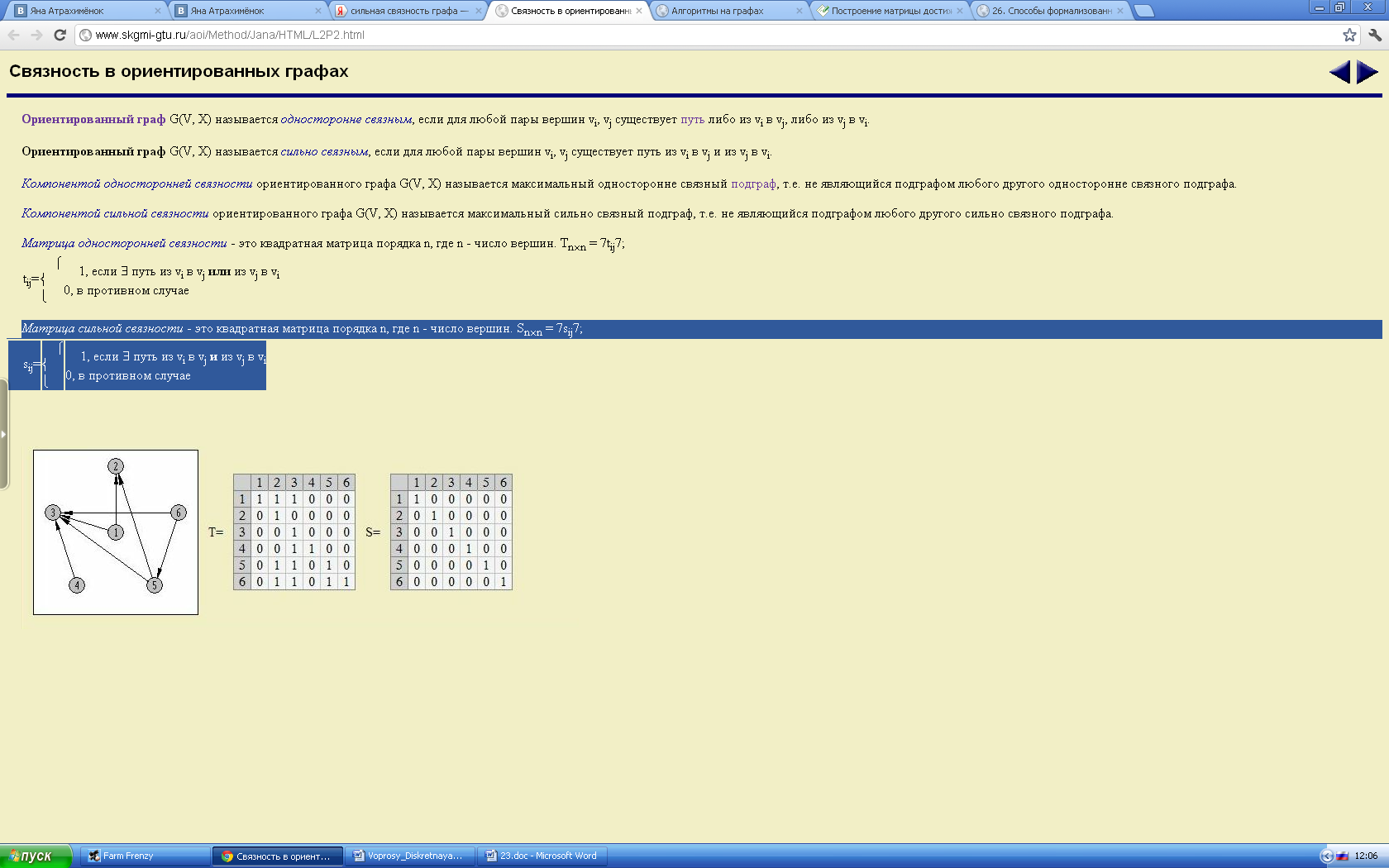
Ориентированный граф G(V, X) называется сильно связным, если для любой пары вершин vi, vj существует путь из vi в vj и из vj в vi.
Компонентой сильной связности ориентированного графа G(V, X) называется максимальный сильно связный подграф, т.е. не являющийся подграфом любого другого сильно связного подграфа.
Матрица сильной связности - это квадратная матрица порядка n, где n - число вершин. Sn*n = 7sij7;
] Поиск в ширину (BFS, Breadth-first search) — метод обхода и разметки вершин графа. Поиск в ширину выполняется в следующем порядке: началу обхода s приписывается метка 0, смежным с ней вершинам — метка 1. Затем поочередно рассматривается окружение всех вершин с метками 1, и каждой из входящих в эти окружения вершин приписываем метку 2 и т. д. Если исходный граф связный, то поиск в ширину пометит все его вершины. Дуги вида (i, i+1) порождают остовный бесконтурный орграф, содержащий в качестве своей части остовное ордерево, называемое поисковым деревом. Легко увидеть, что с помощью поиска в ширину можно также занумеровать вершины, нумеруя вначале вершины с меткой 1, затем с меткой 2 и т. д.
Поиск в глубину (англ. Depth-first search, DFS) — один из методов обхода графа. Алгоритм поиска описывается следующим образом: для каждой непройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них. Используется в качестве подпрограммы в алгоритмах поиска одно- и двусвязных компонент, топологической сортировки.
24. Транзитивное замыкание графа.
Алгоритм 2: (~n4)
Сильная связность. Отношение Пусть
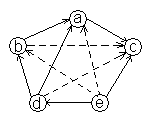
Пример ориентированного графа с тремя компонентами сильной связности. Ориентированный граф Граф сильно связен, если для любых вершин х у существует путь, идущий из х в у.
26. Понятие логической функции. Способы задания логических функций. Логическая функция - это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1. Способы задания функций алгебры логики АЛ Логической функцией называется зависимость поведения выходных логических величин от изменения входных логических величин. Задачей алгебры логики является поиск математического или функционального представления логических функций с целью ее непосредственного использования для управления объектом или процессом. Имеются различные способы представления логических взаимодействий. Табличный способ. При этом способе функция задается в виде таблицы истинности, представляющей собой совокупность всех комбинацийвходных переменных (левые столбцы) и соответствующих им значений функции (правый столбец). Таблица истинности содержит 2n строк, n +m столбцов (количество входов n +количество выходов m). Например: пусть требуется задать функцию двух переменных, т.е. дискретное устройство на два входа и на один выход, следовательно, число столбцов = 2+1, а число строк = 4.
Таблица. 3.2Пример таблицы истинности Таблицы истинности возможно составить по условиям задания. Задание на управление для выше приведенного примера может выглядеть следующим образом: лампа А горит только тогда, когда одновременно нажаты обе кнопки x и y.
Таблицы истинности позволяют автоматизировать поиск искомой логической функции в математическом виде. Словесно-аналитический способ задания функции алгебры логики. При этом способе функция задается в виде аналитического выражения.В левой части высказывания указывается действие управляемого привода (или исполнительного устройства), а в правой части- условие, при котором выполняется это действие. Аналитическое выражение задается в возможно более краткой форме. Некоторые подразумеваемые слова могут опускаться, например, такие как «кнопка», «нажать», «активен» и другие. Название датчиков и кнопок возможно заменять их схемным обозначением. При этом указание на датчик означает то, что этот датчик изменил свое состояние на активное (логическая 1). Ударение делается на союзы предложения, которые, в большинстве случаев, указывают на логическое действие.
В данном примере описана работа распределителя, с помощью которого производиться управление цилиндром.Электромагнит Y1 включиться (соответственно цилиндр начнет свое движение), если будет нажата кнопка S1 и датчикB1 активен. Союз и указывает на логическое взаимодействие сигналов управления от кнопки и датчика. Для поиска несложных логических функций аналитический способ является наиболее простым и быстрым. Однако, этот способ в большей степени основан на интуиции. Поэтому для поиска сложных функций он не используется. Графические способы. Для графического описания логических взаимодействий можно использовать разные способы, предлагаемые стандартом IEC 848: шаговая, временная диаграмма, логические функциональные схемы, функциональный план. При взаимодействии нескольких приводов наиболее наглядным средством установления логических взаимосвязей является шаговая диаграмма. Рис. 3.4 Пример шаговой диаграммы В шаговой диаграмме различают линии состояния или положения привода (в данном случае это линия, описывающая перемещение цилиндра) и линии управляющих сигналов. Отличием от временной диаграммы является то, вместо временной оси здесь использованы шаги- условные временные отрезки. Длина шага не пропорциональна реальному времени, а связанна с одним действием управляемого объекта. Сигналы взаимодействуют друг с другом (сливание потоков информации) по определенному логическому закону. Каждое логическое действие имеет собственное обозначение. Достоинством шаговой диаграммы является наглядность связей взаимодействия приводов и сигналов управления между собой во времени.
Рис. 3.5 Пример временной диаграммы Из диаграммы следует, что лампа Н1 «горит» тогда, когда нажата кнопка S1 и не нажата кнопка S2. Лампа Н2 «горит» тогда, когда нажата кнопка S2 и не нажата кнопка S1. Логические функциональные блок-схемы состоят из логически связанных между собой отдельных функциональных блоков, которые являются обозначениями элементарных логических функций.
Логические функциональные блок-схемы обладают всеми достоинствами графического изображения- это наглядность связей логических функциональных блоков. Недостатком данных схем является сложность прослеживания изменения сигналов во времени. Логические функциональные блок-схемы являются одним из самых распространенных языков программирования в промышленности. Напомним, что целью алгебры логики является получение математического или функционального изображения функции. Функциональный план является графическим средством отображения по-шагового управления процессом. Весь процесс управления разбит на отдельные шаги (минимальные части процесса управления), которые осуществляются при выполнении определенных условий. Функциональный план является языком программиров Рис. 3.6 Пример функционального плана Математическое представление алгебры логики. Элементарные логические действия можно представить с помощью специальных или арифметических символов (AND: , ·;OR: , +; NO:a`), обозначающих логические действия. Используя законы алгебры логики, возможны преобразования математических выражений логических функций.
Булеву функцию можно задать с помощью единичного п – мерного куба (рис. 7).
Рис. 7 Единичным п – мерным кубом называется граф, каждая вершина которого взаимно однозначно соответствует двоичному набору. Две вершины соединены ребром, если соответствующие наборы отличаются только в одном разряде (в одной координате). На рис. 7 показаны п- мерные кубы для булевых функций: двух переменных (а), трех переменных (б), четырех переменных (в). Отметив вершины, в которых булева функция принимает единичные значения, получим геометрическое представление булевой функции. Так функция примет вид:
Часто для изображения булевых функций двух и трех переменных используют прямоугольную систему координат:
Рис. 9 Изображение булевых функций числа переменных более трех в этом случае невозможен. В методе минимизации булевых функций Квайна – Мак- Класки используется кубическое представление булевых функций (аналог п- мерных кубов). Терм максимального ранга принято называть 0-кубом и обозначать К 0. Если два 0-куба из комплекса К 0 различаются только по одной координате, то они образуют куб (отрезок) K 1. 27. Булева алгебра. Основные свойства операций булевой алгебры. Понятие двойственной и самодвойственной логической функции.
Булевой алгеброй называется непустое множество A с двумя бинарными операциями
Некоторые свойства Из аксиом видно, что наименьшим элементом является 0, наибольшим является 1, а дополнение a любого элемента a однозначно определено. Для всех a и b из A верны также следующие равенства:
Основные тождества В данном разделе повторяются свойства и аксиомы, описанные выше с добавлением ещё нескольких. Сводная таблица свойств и аксиом, описанных выше:
Определение. Двойственной для функции f(x1, x2, …, xn) называется функция
Определение. Функция, совпадающая со своей двойственной, называется самодвойственной. Утверждение. Если функция f(x1, x2, …, xn) самодвойственна, то функция Утверждение. Чтобы функция была самодвойственной необходимо и достаточно, чтобы на всяких двух противоположных наборах она принимала разные значения. Противоположными называются те наборы, которые в сумме дают двоичный код числа (2n-1).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1047; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.224.236 (0.012 с.) |



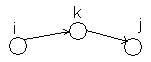

 на вершинах графа называется отношением сильной связности. Сильная связность — отношение эквивалентности. Рассмотрим транзитивность:
на вершинах графа называется отношением сильной связности. Сильная связность — отношение эквивалентности. Рассмотрим транзитивность: 
 — ориентированный граф. Компонентой сильной связности называется класс эквивалентности множества вершин этого графа относительно сильной связности.
— ориентированный граф. Компонентой сильной связности называется класс эквивалентности множества вершин этого графа относительно сильной связности.
 Рис. 3.3 Пример аналитического задания логической функции
Рис. 3.3 Пример аналитического задания логической функции
 Временные диаграммы важны для изображения динамически изменяющихся процессов. Горизонтальная ось является временной. Временные диаграммы удобны для изображения динамических процессов, которые быстро изменяются во времени. Они позволяют визуально анализировать реакцию выходных величин на изменение входных.
Временные диаграммы важны для изображения динамически изменяющихся процессов. Горизонтальная ось является временной. Временные диаграммы удобны для изображения динамических процессов, которые быстро изменяются во времени. Они позволяют визуально анализировать реакцию выходных величин на изменение входных. Рис. 3.5 Пример логической функциональной блок-схемы
Рис. 3.5 Пример логической функциональной блок-схемы ания.
ания.

 Рис. 8
Рис. 8
 (аналог конъюнкции),
(аналог конъюнкции),  (аналог дизъюнкции), унарной операцией
(аналог дизъюнкции), унарной операцией  (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:
(аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:









 ;
;
 ;
;
 ;
;
 ;
;
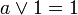 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
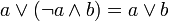 ;
;
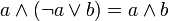 .
.
 ;
;
 .
.

 тоже самодвойственна.
тоже самодвойственна.


