
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие замкнутого класса. Класс монотонных логических функций.Понятие замкнутого класса. Класс линейный логических функций.. ⇐ ПредыдущаяСтр 6 из 6
Замкнутый класс в теории булевых функций — такое множество Классы логических функций Функция, "сохраняющая 0". Это - такая логическая функция, значение которой равно 0, если все аргументы равны 0: f(0,0,...,0) = 0. Примером функции, сохраняющей 0, является функция Функция, "сохраняющая 1". Это - такая логическая функция, значение которой равно 1, если все аргументы равны 1: f(1,1,...,1) = 1. Примером функции, сохраняющей 1, является функция &. "Монотонная" функция. Это - такая логическая функция, которую можно выразить через & и Монотонную функцию можно распознать по ее таблице истинности. Для этого нужно взять все пары строк в таблице, которые отличаются всего в одном столбце (не считая крайнего правого). Например: 0,0,0,0 и 0,0,0,1; 1,0,0,1 и 1,1,0,1. Пусть в одной строке в некотором столбце стоит "0", а в другой строке в этом же столбце стоит "1". Нельзя, чтобы в крайнем правом столбце, где записано значение функции было наоборот: "1", а потом "0". Если такая ситуация нигде не встречается, то функция монотонная, и ее можно выразить через "Линейная" функция. Это - такая логическая функция, которую можно выразить через Чтобы узнать, линейна ли функция, надо выразить ее через полином Жегалкина и посмотреть, не встречается ли там операция &. Если нет, то функция линейна. Для функций от 1 и 2 переменных мы уже приводили формулы, выражающие их через &, Двойственные функции. Логические функции f и g называются двойственными, если f(~x1, ~x2,...,~xN) = ~g(x1, x2,..., xN). Кратко это будем обозначать так: "f" * "g". Двойственные функции легко обнаружить с помощью простого приема. Надо заменить в таблице истинности все "0" на "1", а все "1" на "0". Полученная таблица истинности и будет таблицей двойственной функции. Ниже приведен список двойственных функций для всех унарных и бинарных операций.
"Самодвойственная" функция. Это - логическая функция, которая двойственна самой себе: f(~x1, ~x2,...,~xN) = ~f(x1, x2,..., xN).
37. Теорема о функциональной полноте в слабом смысле. Полнота системы функций означает, что, пользуясь только элементами соответствующих этим функциям типов, можно собрать любую логическую схему. При схемной реализации константы 0 и 1 специальных элементов не требуют. Поэтому существует ослабленное понятие функциональной полноты. Определение. Система функций S называется полной в слабом смысле, если система Теорема 1. (Поста). Для того, чтобы система функций S была полной в слабом смысле необходимо и достаточно, чтобы она содержала хотя бы одну нелинейную функцию и хотя бы одну немонотонную функцию. Теорема 2. (Пост). Для того, чтобы система функций была полной (в сильном смысле) необходимо и достаточно, чтобы она не содержалась целиком ни в одном из замкнутых классов K0, K1, KS, KM и KL. Схема доказательства. Необходимость очевидна, поскольку никакой из перечисленных классов не совпадает целиком с множеством всех булевых функций. Достаточность доказывается в 3 этапа: 1. построение констант 0 и 1 с помощью функций 2. построение функции–отрицания с помощью констант 0, 1 и 3. построение конъюнкции с помощью констант 0, 1, функции После этого учитывая, что дизъюнкция представляется через конъюнкцию и отрицание Замечание. Из теоремы, в частности, следует, что всякий замкнутый класс, отличный от множества всех булевых функций, содержится в одном из классов K0, K1, KS, KM, KL. По этой причине перечисленные классы называют основными замкнутыми классами пространства булевых функций. Пример. Рассмотрим совокупность булевых функций
Из таблицы видно, что множество функций S не содержится полностью ни в одном из пяти основных замкнутых классов (нет ни одного столбца целиком заполненного символами «+»). Следовательно, система функций S является полной (в сильном смысле), а совокупность
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 401; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.199.50 (0.008 с.) |
 функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим:
функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим:  . Другими словами, любая функция, которую можно выразить формулой с использованием функций множества
. Другими словами, любая функция, которую можно выразить формулой с использованием функций множества  .
. , 0 и 1.
, 0 и 1. "
"  "
"  "
"  "
" является полной (в сильном смысле, т. е. в смысле определения в пункте 1).
является полной (в сильном смысле, т. е. в смысле определения в пункте 1). ,
,  и
и  ;
; функции;
функции; и
и  .
. и что система
и что система 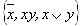 полная, достаточность доказана.
полная, достаточность доказана. . Составим и заполним следующую таблицу, отмечая знаком «+» функции, принадлежащие соответствующим классам. Заполнение первых трех строчек очевидно. Кроме того, непосредственно видно, что функция
. Составим и заполним следующую таблицу, отмечая знаком «+» функции, принадлежащие соответствующим классам. Заполнение первых трех строчек очевидно. Кроме того, непосредственно видно, что функция  сохраняет константы 0 и 1. Уже по форме записи она является линейной. Самодвойственоость функции
сохраняет константы 0 и 1. Уже по форме записи она является линейной. Самодвойственоость функции  – полная в слабом смысле.
– полная в слабом смысле.


