
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямое произведение множеств.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Прямым (декартовым) произведением множеств А и В называется множество всех пар (а, в) таких, что а Обозначение: А Если А = В, то А Приведем формулировку определения прямого произведения n множеств: Прямое произведение множеств А1, А2, …, Аn есть множество всех векторов (а1, а2, а3,…, аn) длины n таких, что а1 Если А1 = А2 = … = Аn, то А1 Теорема о мощности прямого произведения множеств. Пусть Тогда мощность прямого произведения Доказательство методом математической индукции. Для По предположению Таким образом, из всех Следствие: Понятие соответствия между множествами. Определение. Соответствием между множествами А и В называется некоторое подмножество G их декартова произведения: G= А Если (a;b) Соответствие называется полностью определённым, если, то есть каждый элемент множества имеет хотя бы один образ во множестве; в противном случае соответствие называется частичным. Соответствие называется сюръективным, если, то есть если каждому элементу множества соответствует хотя бы один прообраз во множестве. Соответствие называется функциональным (однозначным), если любому элементу множества определения соответствует единственный элемент множества значения. Соответствие называется инъективным, если оно является функциональным, и при этом каждый элемент множества имеет не более одного прообраза. Соответствие называется взаимнооднозначным (биективным), если любому элементу множества соответствует единственный элемент множества, и наоборот. Можно сказать также, что соответствие является взаимнооднозначным, если оно является полностью определённым, сюръективным, функциональным, и при этом каждый элемент множества имеет единственный прообраз. 4. Понятие отображения множеств. Одним из важных понятий математики, есть понятие отображения, которое непосредственно связано с понятием соответствия, описывая его. Понятие отображения часто ассоциируется с понятием функции. Для задания отображения f необходимо указать: 1. Область определения – множество, которое отображается. Область определения задается изначально. Обозначается D(f). Элементы области определения называют аргументами. 2. Область значений – множество, к которое или на которое отображается заданная область. Область значений. Обозначается E(f) Правило (закон, соответствие) между D(f) и E(f). Отображения можно записывать в т виде: f:A→B,, B=f(A), B=F(A), y=f(x) и др. При отображении, в том числе и однозначном отображении, количество образов равно или меньше числа прообразов. Это следует из того, что несколько элементов из области определения могут отобразиться в один и тот же элемент множества значений. Задание отображений. Для задания (записи) отображений используются следующие основные способы: Аналитический способ – в виде формулы. Табличный способ. В первой строчке таблицы записываются элементы (числа) области определения, во второй – элементы множества значений. Графический способ – на координатной плоскости. С помощью графов - двух кругов или иных геометрических фигур и стрелок. Словесный способ – в виде текста, описывающего закон соответствия Виды отображений. Отображения делятся на два вида: отображения “в” и “на”. Пусть задано отображение B=f (A) 1. Отображение “в” – инъекция. Соответствие, при котором каждому элементу множества A соответствует единственный элемент множества B, а каждому элементу множества B соответствует не более одного прообраза из A. При этом, мощность множества A меньше мощности множества B. 2. Отображение “на” – сюръекция. Соответствие, при котором каждому элементу множества A соответствует единственный элемент множества B, а каждому элементу множества B соответствует хотя бы один прообраз из A. При этом, мощность множества A больше или равна мощности множества B. Особое место занимают взаимнооднозначные отображения (соответствия). Взаимнооднозначное отображение (соответствие) – биекция. Соответствие, при котором каждому элементу множества A соответствует единственный элемент множества B и каждому элементу множества B соответствует один прообраз из множества A. При этом мощность множества A равна мощности множества B. Множества будут равномощными (равносильными, эквивалентными), если между ними можно установить (задать) взаимнооднозначное соответствие. Для взаимнооднозначных отображений, обратное отображение также является взаимнооднозначным отображением.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 827; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.158.29 (0.008 с.) |

 А и в
А и в  В.
В. А1, а2
А1, а2  Аn.
Аn. - конечные множества. Соответственно мощности этих множеств равны:
- конечные множества. Соответственно мощности этих множеств равны: 
 множеств равна произведению мощностей соответствующих множеств, т.е.
множеств равна произведению мощностей соответствующих множеств, т.е. 
 теорема тривиально верна. Предположим, что она верна и для
теорема тривиально верна. Предположим, что она верна и для  и докажем ее справедливость для
и докажем ее справедливость для 
 . Возьмем любой вектор
. Возьмем любой вектор  из
из 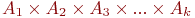 и припишем справа элемент
и припишем справа элемент  . Это можно сделать
. Это можно сделать  способом, т. е. получим
способом, т. е. получим  .
. векторов приписыванием справа элемента из
векторов приписыванием справа элемента из  можно получить
можно получить  векторов, причем все они различны. Поэтому для
векторов, причем все они различны. Поэтому для 
 , то говорят, что b соответствует a при соответствии | А
, то говорят, что b соответствует a при соответствии | А 


