
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие операции, ассоциативной операции, дистрибутивной операции. Понятие алгебры, алгебраической системы, модели. Понятие группоида, полугруппы, коммутативной полугруппы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Говорят, что на множестве X определена алгебраическая операция (*), если каждой упорядоченной паре элементов поставлен в соответствие некоторый элемент,называемый их произведением. Ассоциати́вная опера́ция — это бинарная операция Дистрибути́вность — свойство согласованности двух бинарных операций, определённых на одном и том же множестве. Говорят, что две бинарные операции + и × удовлетворяют свойству дистрибутивности, если для любых трех элементов
Алгеброй А называется совокупность множества М с заданными в нем операциями. А=(M,S), где M- носитель,S-сигнатура(множество различных операций). Алгебраической системой <M;S; O > называется объект, состоящий из трёх множеств: непустого множества M, множества алгебраических операций S, определёных на M, и множества отношений O, определёных на M. Множество M называется носителем алгебраической системы. Если алгебраическая система не содержит операций, она называется моделью, если не содержит отношений, то – алгеброй. Алгебра А=<M,*> с одной бинарной операцией называется группоид. Полугруппа - алгебра с одной бинарной операцией, в которой операция ассоциативна: А=<M,*>, Коммутативная полугруппа (абелева полугруппа)- алгебра с одной бинарной операцией, в которой операция ассоциативна и коммутативна: А=<M,*>, 1. 2. Понятие группы. Группа подстановок. Группой(А=<M,*>) называется множество элементов, на котором задана операция умножения, которая удовлетворяет следующим четырём аксиомам: Группа подстановок -совокупность подстановок на некотором множестве X, образующих группу относительно операции умножения подстановок. Иначе, группа подстановок.- это пара (G, X), где G - группа, X - множество и каждому
Понятие кольца. Кольцо вычетов. Определение кольца Кольцом
Пример 5.8.Все целые положительные и отрицательные числа и нуль образуют коммутативное кольцо с единицей относительно обычных операций сложения и умножения. Пример 5.9.Легко убедиться, что полная система вычетов по модулю Кольцо вычетов по модулю При описании блочных кодов [25, 30, 33] широко используется понятие кольца вычетов по модулю некоторого полинома Для полиномов существуют понятия, аналогичные введенным в 5.8 для чисел, если заменить в этих понятиях слово «число» словом «полином». Так, если при делении полиномов Все полиномы, сравнимые между собой по модулю Совокупность классов вычетов по модулю Пример 5.13.Рассмотрим кольцо классов вычетов по модулю полинома
Здесь 10. Определение поля Полем Другими словами, полем называют множество, которое является аддитивной абелевой группой; ненулевые же элементы этого множества образуют мультипликативную абелевую группу, и выполняется закон дистрибутивности. По аналогии с группами число элементов поля называется порядком поля. Поля, порядки которых конечны, называются конечными полями. Конечные поля имеют наибольшее значение в теории кодирования. Отметим некоторые свойства полей, вытекающие из их определения. 1. Для любого элемента поля 2. Для ненулевых элементов 3. Для любых элементов 4. Если Пример 5.10Множество всех действительных чисел образует поле. Существует также поле комплексных чисел, поле рациональных чисел, но не может быть поля целых чисел, поскольку обратные элементы по умножению, кроме единицы, не являлись бы целыми. Пример 5.11. Множество чисел Пример 5.12.При
Перестановки Перестановки. Перестановкой называется расположение элементов множества в определенном порядке. Теорема. Число перестановок n -элементного множества S, т.е. число способов его упорядочивания выражается формулой Pn=n!. Символом n! обозначается произведение натуральных чисел от 1 до n: n!=1×2×...× n. Считается, что 0!=1. Доказательство. Будем последовательно выбирать элементы множества S и располагать их в определенном порядке на n местах. На первое место можно поставить любой из n элементов. После того, как заполнено первое место, на второе место можно поставить любой из оставшихся n -1 элементов и т.д. Тогда по правилу произведения все n мест можно заполнить n ×(п -1)×(п -2)×...×2×1= n! способами. Следовательно, n -элементное множество можно упорядочить n! способами.
Перестановки с повторениями Перестановки с повторениями. Перестановкой с повторениями называется расположение элементов мультимножества в определенном порядке. Теорема. Число перестановок с повторениями для мультимножества где Доказательство 1. Рассмотрим одну перестановку мультимножества и заменим в ней все одинаковые элементы разными. Тогда, число различных перестановок, которые можно составить из рассматриваемой перестановки, равно k 1!× k 2!×…× km!. Проделав это для каждой перестановки, получим n! перестановок. Следовательно, Cn (k 1, k 2,…, km)× k 1!× k 2!×…× km!= n!, Число Cn (k 1, k 2,…, km) называется полиномиальным коэффициентом. Приведем еще одно доказательство данной теоремы. Доказательство 2. Для упорядочивания мультимножества необходимо из n мест выбрать k 1 мест для элемента s 1, что можно сделать
13. Понятие сочетания. Теорема о числе сочетаний из n элементов по k. Свойства сочетаний. Сочетанием из n элементов по m (иногда читают просто: из n по m) называется m-элементное подмножество некоторого n-элементного множества. Теорема. Число сочетаний из n элементов по k определяется по формуле:
Свойства сочетаний
Первое свойство непосредственно вытекает из формул:
Доказательство: Составим 1-й класс - сочетания, содержащие элемент 2-й класс - сочетания, не содержащие элемент Если из любого сочетания 1-го класса откинуть элемент Сочетания 2-го класса являются
Доказательство:
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.119.67 (0.007 с.) |

 , обладающая ассоциативностью или сочетательностью:
, обладающая ассоциативностью или сочетательностью:  для любых элементов
для любых элементов  .
. :
: — дистрибутивность слева;
— дистрибутивность слева; — дистрибутивность справа.
— дистрибутивность справа.

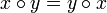




 соответствует подстановка
соответствует подстановка  множества X такая, что 1)
множества X такая, что 1)  ,
,  , и 2) х a =х для любого
, и 2) х a =х для любого  тогда и только тогда, когда a=e - единица группы G
тогда и только тогда, когда a=e - единица группы G называется множество элементов, на котором определены две операции – сложение и умножение, и в
называется множество элементов, на котором определены две операции – сложение и умножение, и в 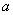 и
и  из
из  (замкнутость операции умножения).
(замкнутость операции умножения).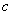 из
из  и
и  .
. и
и  .
. также образует коммутативное кольцо с единицей относительно операций сложения и умножения по модулю
также образует коммутативное кольцо с единицей относительно операций сложения и умножения по модулю  .
.
 .
.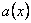 и
и  из
из  на
на 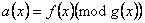 .
. над двоичным полем. Полиномы вида
над двоичным полем. Полиномы вида 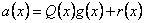 , где
, где  – произвольный полином, степень которого меньше 2, при фиксированном
– произвольный полином, степень которого меньше 2, при фиксированном 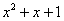 . Так как всего имеется 4 разных полинома
. Так как всего имеется 4 разных полинома 


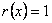





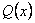 – произвольный полином. В качестве представителей классов обычно выбирают вычеты наименьшей степени, которые совпадают с полиномами
– произвольный полином. В качестве представителей классов обычно выбирают вычеты наименьшей степени, которые совпадают с полиномами  .
. .
. .
. .
. и
и  , то
, то  .
. , где
, где  имеем простейшее двоичное поле, состоящее из двух элементов 0 и 1. Эти элементы являются соответственно единичными элементами относительно операций сложения и умножения по модулю 2, которые определяются правилами:
имеем простейшее двоичное поле, состоящее из двух элементов 0 и 1. Эти элементы являются соответственно единичными элементами относительно операций сложения и умножения по модулю 2, которые определяются правилами:  ;
; 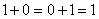 ;
;  ;
;  ;
;  . Так как
. Так как  , то операции сложения и вычитания в двоичном поле совпадают, а так как
, то операции сложения и вычитания в двоичном поле совпадают, а так как  , также совпадают операции умножения и деления. Это поле находит широкое применение в теории и технике помехоустойчивого кодирования.
, также совпадают операции умножения и деления. Это поле находит широкое применение в теории и технике помехоустойчивого кодирования. выражается формулой
выражается формулой ,
, .
.
 способами, затем из n - k 1оставшиеся мест выбрать k 2 мест для элемента s 2, что можно сделать
способами, затем из n - k 1оставшиеся мест выбрать k 2 мест для элемента s 2, что можно сделать  способами и т.д. Тогда число способов упорядочивания мультимножества S по правилу произведения равно (напомнив, что 0!=1)
способами и т.д. Тогда число способов упорядочивания мультимножества S по правилу произведения равно (напомнив, что 0!=1)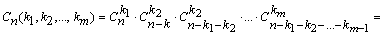
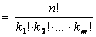 .
.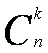 =
=  .
.
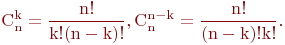
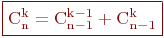
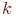 -элементные сочетания из
-элементные сочетания из  элементов
элементов  и разобьем их на два класса:
и разобьем их на два класса: ;
; сочетание из
сочетание из  , их число
, их число  .
. . Поскольку любое
. Поскольку любое  принадлежит одному и только одному из этих классов, а общее число равно
принадлежит одному и только одному из этих классов, а общее число равно  , то приходим к равенству
, то приходим к равенству
 - это число всех
- это число всех  элементов 2-го типа. Размещения k-го класса - это не что иное, как всевозможные перестановки из
элементов 2-го типа. Размещения k-го класса - это не что иное, как всевозможные перестановки из 



