
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равносильные формулы логики предикатовСодержание книги
Поиск на нашем сайте
1. Две формулы A и B логики предикатов называются равносильными на области M, если они принимают одинаковые логические значения для всех значений, входящих в них переменных, принадлежащих области M. 2. Две формулы A и B логики предикатов называются равносильными, если они равносильны на всякой области. Как и в алгебре логики, для равносильности формул используют обозначение К сказанному нужно добавить, что все равносильности алгебры логики будут верны, если в них вместо высказываний подставить формулы логики предикатов. В логике предикатов, кроме равносильностей, аналогичных равносильностям алгебры логики, имеются еще собственные равносильности, не имеющие аналогов в алгебре логики. Эти дополнительные равносильности обусловлены кванторными операциями. Приведем основные из этих равносильностей. Пусть A(x) и B(x) - переменные предикаты, а C - переменное высказывание, тогда имеют место следующие равносильности: 1) 2) 3) 4) 5) 6) 7) 8) 9) Равносильности 6 - 8 говорят о том, что переменное высказывание можно вносить под знак квантора всеобщности и выносить из-под знака этого квантора в конъюнкции, дизъюнкции и импликации. Несколько особой в этом смысле является равносильность 9. В ней переменное высказывание вносится под квантор
Последняя формула получена на основании равносильности 7. Далее:
10) 11) 12) 13) 14) Равносильности 11 - 13 говорят о том, что переменное высказывание можно вносить под знак квантора существования и выносить из-под этого квантора в конъюнкции, дизъюнкции и импликации. Так же, как и равносильность 9, равносильность 14 является особой. В ней переменное высказывание вносится под квантор
15) 16) Приведем обоснование некоторых из этих равносильностей. Однако сразу же нужно отметить, что если в алгебре логики для установления равносильности двух формул мы использовали либо алгебраическое преобразование формул, либо строили для них таблицы истинности, то в алгебре предикатов такой подход не приемлем. Это объясняется тем, что в алгебре логики можно было легко перебрать всевозможные наборы логических значений высказываний, так как каждое из них принимает всего два значения: 0 либо 1. В алгебре предикатов логическое значение предиката зависит уже от переменных, принимающих значения не из множества Поэтому в алгебре предикатов при установлении тех или иных их свойств в основном пользуются непосредственными рассуждениями, применяя аксиомы и законы алгебры логики. Так, равносильность 1 означает тот простой факт, что если не для всех x истинно A(x), то существует x, при котором будет истинным противоположный предикат Аналогично равносильность 2 означает тот простой факт, что если не существует Равносильности 3 и 4 получаются из равносильностей 1 и 2 соответственно, если над обеими их частями выполнить операцию отрицания, а затем воспользоваться законом двойного отрицания:
Приведем рассуждения, обосновывающие равносильность 5. Если оба предиката A(x) и B(x) тождественно истинные, то будет тождественно истинным и предикат
Эти два высказывания являются соответственно левой и правой частями равносильности 5, т.е. в этом случае обе части равносильности 5 принимают значение “истина”. Но может быть и другой случай, когда хотя бы один из предикатов A(x) или B(x) будет не тождественно истинным. Пусть, например, A(x) не тождественно истинный предикат. Тогда не тождественно истинным будет и предикат
т.е. и в этом случае обе части равносильности 5 принимают одинаковые (ложные) значения. Рассмотренные два случая представляют всевозможные “комбинации” логических значений высказываний, входящих в левую и правую части равносильности 5, которые являются одновременно или истинными, или ложными. А это и означает их равносильность. Еще более “длинно” доказывается равносильность формул, содержащих переменные высказывания и предикаты. Здесь надо проанализировать логические значения формул при двух логических значениях переменного высказывания и определенных предположениях о логических значениях предикатов и высказываний, полученных путем связывания переменных кванторами. Таковыми, например, являются равносильности 8, 9, 13 и 14. Докажем равносильность 8. Пусть переменное высказывание Пусть теперь переменное высказывание C принимает значение “истина”. Если при этом предикат B(x) является тождественно истинным, то будет тождественно истинным и предикат Осталось рассмотреть один случай, когда предикат B(x) не является тождественно истинным. Тогда не будет тождественно истинным и предикат Следовательно, и в этом случае обе части равносильности 8 принимают одинаковые (ложные) значения. Таким образом, мы установили, что левая и правая части равносильности 8 принимают во всех случаях одинаковые логические значения, или, иначе, равносильность 8 истинна. Аналогично доказываются и остальные из перечисленных равносильностей. Особый интерес представляют две последние равносильности –15 и 16. Казалось бы, что в дизъюнкции, образованной двумя высказываниями, каждое из которых получено путем применения квантора Однако левую часть каждой из этих неравносильностей можно видоизменить так, что вынесение кванторов за скобки станет возможным. Для этого нужно предварительно переименовать переменные. Это можно делать, так как обозначение переменной в предикате произвольно. Поэтому высказывания Далее, анализируя равносильности 5, 6 и 7, видим, что квантор Таким образом, можно записать последовательность равносильных преобразований:
Этим, собственно говоря, и доказывается равносильность 15. Точно так же доказывается равносильность 16. Только в этом случае следует обратить внимание на равносильности 10, 11 и 12, указывающие на то, в каких случаях можно выносить за скобки квантор существования Исходя из этого, можно записать последовательность равносильных преобразований:
Это и доказывает равносильность 16. Упражнения 1. Какие из следующих выражений являются формулами логики предикатов (в каждой формуле выделите свободные и связанные переменные): 1) 4) 2. Найти отрицание следующих формул: 1) 3) 5) 7) 8) 3. Какие из следующих предложений истинны и какие ложны, если предикат 1) 5) 4. Пусть предикат B(x,y) определен на множестве 1) 5. Пусть A (x) и B (x) - любые предикаты. Какие из следующих формул равносильны формуле 1) 5) 6. Доказать, что для любой формулы логики предикатов можно построить равносильную ей формулу, не содержащую: 1) кванторов существования; 2) кванторов всеобщности.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1714; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.88.18 (0.006 с.) |

 .
.

 ;
;
 ;
;
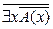 ;
;
 ;
; – эта равносильность свиде-тельствует о том, что квантор всеобщности можно вносить и выносить за скобки в конъюнкции;
– эта равносильность свиде-тельствует о том, что квантор всеобщности можно вносить и выносить за скобки в конъюнкции; ;
; ;
;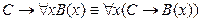 ;
; .
. (правая часть этой равносильности), а выносится квантор
(правая часть этой равносильности), а выносится квантор  (левая часть этой равносильности). Покажем, что это правильно, и одновременно отметим, что в некоторых учебных пособиях ошибочно в этой равносильности переменное высказывание вносится и выносится из-под одного и того же квантора
(левая часть этой равносильности). Покажем, что это правильно, и одновременно отметим, что в некоторых учебных пособиях ошибочно в этой равносильности переменное высказывание вносится и выносится из-под одного и того же квантора  .
.
 , т.е. квантор существования можно вносить и выносить за скобки в дизъюнкции;
, т.е. квантор существования можно вносить и выносить за скобки в дизъюнкции; ;
; ;
; ;
; .
. , а выносится из-под квантора
, а выносится из-под квантора 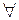 . Покажем, что это действительно так:
. Покажем, что это действительно так: . На основании равносильности 12 имеем
. На основании равносильности 12 имеем .
. ;
; .
. , а из множеств различной природы, в том числе из бесконечных дискретных и непрерывных множеств. Построить же такие таблицы истинности невозможно, так как такие таблицы должны иметь неограниченные размеры.
, а из множеств различной природы, в том числе из бесконечных дискретных и непрерывных множеств. Построить же такие таблицы истинности невозможно, так как такие таблицы должны иметь неограниченные размеры.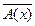 .
. , при котором истинно A (x), то для всех
, при котором истинно A (x), то для всех  ;
; .
. , а поэтому будут истинными высказывания
, а поэтому будут истинными высказывания ;
;  .
. ,
,  и
и  ,
, принимает значение “ложь”. Тогда тождественно истинным будет предикат
принимает значение “ложь”. Тогда тождественно истинным будет предикат  , так как в таком случае исключается из рассмотрения единственная импликация
, так как в таком случае исключается из рассмотрения единственная импликация  , когда она принимает ложное значение. Очевидно, что истинными будут и высказывания
, когда она принимает ложное значение. Очевидно, что истинными будут и высказывания  и
и 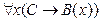 (по тем же причинам). То есть в этом случае обе части равносильности 8 принимают одинаковые логические значения “истина”.
(по тем же причинам). То есть в этом случае обе части равносильности 8 принимают одинаковые логические значения “истина”. ), а значит, истинными будут и высказывания
), а значит, истинными будут и высказывания  ,
,  , а
, а  ,
,  , аналогично в конъюнкции
, аналогично в конъюнкции  , т.е. в таких формулах нельзя выносить за скобки и вносить в них кванторы
, т.е. в таких формулах нельзя выносить за скобки и вносить в них кванторы 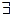 !
! - равносильны.
- равносильны. .
. .
. .
. ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5) 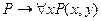 ; 6)
; 6)  ?
? ; 2)
; 2)  ;
; ; 4)
; 4)  ;
; ; 6)
; 6) 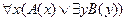 ;
;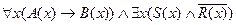 ;
; .
. определен на множестве
определен на множестве 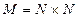 и означает “x<y”:
и означает “x<y”: ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;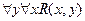 ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  ?
? ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ?
?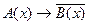 :
: ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
; ; 6)
; 6)  ; 7)
; 7) 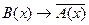 ?
?


