
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интуитивное понятие алгоритмаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Слово алгоритм связывают с именем среднеазиатского математика IX века аль-Хорезми в его латинском написании – algorithmi (иногда употребляется равнозначное слово алгорифм). Для многих задач решение дается в виде формулы, которая определяет последовательность математических операций для получения искомого результата. Например, формула корней квадратного уравнения позволяет найти их по значениям коэффициентов этого уравнения, формула Герона выражает площадь треугольника через длины его сторон и т.д. Однако нам известны многочисленные задачи, для которых ответ может быть легко найден, хотя он и не записывается в виде формулы. Таковыми являются арифметические правила сложения, вычитания, умножения и деления чисел, позволяющие получить сумму, разность, произведение и частное двух (или большего количества) чисел, правило извлечения квадратного корня, правило отыскания наибольшего общего делителя, правила перевода чисел из одной системы счисления в другую и т.д. При решении подобных задач мы уже не пользуемся какой-то одной формулой, а используем некоторую совокупность действий (правило) в строго определенной последовательности с целью получения искомого результата. Такую систему правил называют алгоритмом. Надо сказать, что слово алгоритм стало настолько модным, что им стали называть не только сугубо математические правила, но и рецепты приготовления блюд, технологические процессы варки в мартеновских печах стали и т.п. В каждом из рассмотренных примеров задач исходные данные могут изменяться в широких пределах, но система правил при этом не меняется. Поэтому принято говорить о классе однотипных задач или о массовой проблеме. Следует отметить, что алгоритмы решения многих математических задач, для которых не удается получить ответ в виде формулы, основаны на следующей процедуре: строится бесконечный процесс, сходящийся к искомому решению. Но так как вычисления нельзя продолжать бесконечно долго, то этот процесс обрывается на некотором шаге, а полученная на последнем шаге величина принимается за приближенное решение рассматриваемой задачи. При этом необходимо, чтобы процесс решения был сходящимся. Тогда это будет гарантией того, что для любой заданной точности Исходя из всего сказанного, интуитивное определение понятию алгоритма можно дать следующее. Алгоритмом называется общий, единообразный, точно установленный способ решения любой задачи из данной массовой проблемы. Такое определение алгоритма нельзя считать строгим, так как. в нем используются слова, точный смысл которых не установлен. Это касается слова способ. В связи с этим такое нестрогое определение алгоритма называют интуитивным. Несмотря на это, можно отметить некоторые характерные черты алгоритма. 1. Дискретность алгоритма. Каждая последующая совокупность величин получается из совокупности предыдущих величин в дискретные моменты времени, иначе говоря, алгоритм расчленяется на отдельные элементарные и легко осуществимые акты. 2. Детерминированность алгоритма. Совокупность величин, получаемых в какой-то неначальный момент времени, определяется совокупностью величин, полученных в предшествующие моменты времени. 3. Элементарность шагов алгоритма. Закон получения последующей совокупности величин из предыдущей должен быть простым. 4. Массовость алгоритма. Начальная совокупность величин может варьироваться в бесконечных пределах. 5. Результативность алгоритма. Последовательный процессполучения совокупности величин должен быть конечным и должен давать ожидаемый результат. Интуитивное понятие алгоритма с его характерными чертами в течение долгого времени удовлетворяло математиков. Такое определение алгоритма было допустимо, пока оно применялось к уже найденному алгоритму решения некоторой задачи. Положение существенно меняется, когда возникает алгоритмическая проблема, решение которой неизвестно. В этом случае надо либо доказать существование алгоритма, либо доказать его отсутствие. Если алгоритм решения задачи существует в принципе, то проще доказать его существование, чем его отсутствие. В первом случае достаточно и интуитивного, нестрогого определения алгоритма. Во втором случае необходимо иметь точное формальное определение алгоритма. В связи с существованием алгоритмически не решенных проблем усилия некоторых математиков-профессионалов были направлены на уточнение понятия алгоритма. Уточнение понятия алгоритма В истории математики известны случаи длительных и безуспешных попыток поиска алгоритмов решения тех или иных задач. Одним из таких примеров является Великая теорема Ферма (сформулированная французским математиком П. Ферма примерно в 1630 г.): для любого натурального числа
не имеет решений в целых положительных числах До настоящего времени не известен алгоритм, позволяющий для произвольного В алгоритмических проблемах речь обычно идет о существовании алгоритма для вычисления целочисленных значений функции, зависящей от целочисленного значения аргументов. Такие функции называют числовыми. Именно такой является функция, рассмотренная выше в теореме Ферма. Рассмотрение в алгоритмических проблемах именно числовых функций может быть легко обосновано. Действительно, в математике большинство рассматриваемых функций определены на континуальных (от лат. continuum – непрерывное) множествах, например на множестве точек некоторого отрезка. В то же время на практике любая величина может быть измерена с ограниченной точностью, причем это ограничение точности является принципиальным. И определяется оно конечной разрешающей способностью измерительных приборов, вследствие чего множество значений любой физической величины является счетным (конечным). Все эти значения измеряемой физической величины мы можем перенумеровать целыми числами и свести, таким образом, алгоритм вычисления любой имеющей практическое значение функции к алгоритму вычисления числовой функции. Числовые функции, значения которых можно вычислить посредством применения некоторого алгоритма, называются эффективно вычислимыми (или просто вычислимыми) функциями. Поскольку понятие алгоритма в этом определении остается интуитивным, то и понятие вычислимой функции оказывается интуитивным. Функции, определенные не для всех значений аргументов, называются частичными (не всюду определенными) функциями. Функция называется всюду определенной, если область ее определения, т.е. множество С.К. Клини (американский логик и математик) высказал гипотезу о том, что класс алгоритмически вычислимых частичных функций совпадает с классом всех частично рекурсивных функций. Ранее аналогичную гипотезу относительно всюду определенных вычислимых функций выдвинул А Чёрч (американский логик и математик). Гипотезы Чёрча и Клини обычно объединяют в виде тезиса Чёрча. Австрийский логик и математик К. Гёдель впервые описал класс всех рекурсивных функций как класс всех числовых функций, определяемых в некоторой формальной системе. На основании тезиса Чёрча вопрос о вычислимости функции, имеющей нестрогое интуитивное понятие, тем не менее равносилен вопросу о ее рекурсивности. Но понятие рекурсивности – строгое, поэтому в определенных случаях можно доказать, что если решающая задачу функция не является рекурсивной, то и алгоритм ее вычисления не может быть построен. Точное описание класса частично-рекурсивных функций совместно с тезисом Чёрча дает одно из возможных решений задачи об уточнении понятия алгоритма. Другое решение было найдено Постом (американский логик и математик) и Тьюрингом (английский математик) независимо друг от друга. Основная мысль их заключается в том, что процессы, описываемые алгоритмами, может выполнять соответствующая машина. Тьюрингом и Постом были описаны в точных математических терминах классы машин, на которых можно осуществить или имитировать практически все алгоритмические процессы, которые когда-либо описывались математиками. Такие машины сейчас называют машинами Тьюринга. Исследования показали, что класс функций, вычислимых на машинах Тьюринга, в точности совпадает с классом всех частично- рекурсивных функций. Тем самым было получено еще одно подтверждение тезиса Чёрча. Еще одним уточнением понятия алгоритма является понятие нормального алгоритма Маркова. В алгоритме Маркова исходные данные для вычислительного процесса записываются в виде слова – последовательности букв – символов. Вычислительный процесс сводится к преобразованию слов в соответствии с заданной программой. Оказалось, что класс функций, вычислимых с помощью нормальных алгоритмов, совпадает с классом частично-рекурсивных функций. Таким образом, все известные уточнения понятия алгоритма приводят к одному и тому же классу функций – частично-рекурсивным функциям. Это доказывает эквивалентность перечисленных уточнений.
4. 3. Частично - рекурсивные и общерекурсивные функции Простейшими эффективно вычислимыми функциями принято считать следующие три числовые функции: 1) 2) 3) Иногда данные функции называют соответственно: оператор сдвига, оператор аннулирования и оператор проектирования. Все эти три функции всюду определены и интуитивно вычислимы. Для построения частично-рекурсивных функций вводится три основных операции над простейшими функциями. Рассмотрим каждую из них. 1. Операция суперпозиции функций (составление из двух и более функций одной сложной функции, или, то же самое, что подстановка функции в функцию). Пусть даны функции
Говорят, что функция Очевидно, что если все функции Приведем примеры построения постоянных функций, принимающих значения 1 и 2, путем применения операции суперпозиции к простейшим числовым функциям
Так как простейшие функции являются всюду определенными и интуитивно вычислимыми, то, очевидно, функции 2. Операция (схема) примитивной рекурсии. Центральное место в построении частично-рекурсивных функций занимает операция, или так называемая схема примитивной рекурсии (СПР). Она задается следующим образом. Пусть имеются две функции
Нетрудно заметить, что функция Очевидно, что если функции
и т.д. Тем самым рекурсивно получаем значения функции В частности, если функция
Если же функция
где a – любое постоянное число. Ранее мы уже определили частично-рекурсивную функцию как функцию, которая получается за конечное число шагов из простейших функций Если функция частично-рекурсивна и всюду определена, то она называется общерекурсивной. Рассмотрим примеры приведения некоторых функций к примитивно рекурсивной форме с последующим вычислением значений этих функций. Пример. 1. Пусть функция
Очевидно, что в этой системе равенств По определению примитивной рекурсии Таким образом, исходную функцию
Вычислим Из первого равенства системы (5), изменяя x от 0 до 2, получим Из второго равенства системы (5) и из того, что
Представляет интерес вопрос определения аналитического вида функции
Проделав эту операцию 3. Операция минимизации (μ-оператор). Пусть дана некоторая функция Для функции
Получать функцию 1. Вычислим 2. Вычислим Этот процесс будет продолжаться до тех пор, пока не найдется значение Пример 2. Функцию
Таким образом,
Упражнения 1) Пусть функция
Привести эту функцию к СПР; используя полученную СПР, вычислить 2) Доказать общерекурсивность функции 3) Функцию 4) Представить функцию 5) Определить аналитический вид функции, если в соответствующей СПР
4. 4. Машины Тьюринга В понятии “машина Тьюринга” не следует искать некоторый материальный объект − вычислительное устройство в общепринятом смысле. Это абстрактная вычислительная машина, концепция которой возникла в середине 30-х годов XX века у английского математика А. Тьюринга в результате произведенного им анализа действий человека, осуществляющего в соответствии с заранее разработанным планом поиск численного решения той или иной задачи. Этот анализ стимулировался желанием разрешения назревшей к тому времени проблемы поиска точной математической формулировки понятия алгоритма, в качестве которого до работ Тьюринга использовалось интуитивное понятие. Тьюрингом был сформулирован тезис: всякая интуитивно вычислимая функция может быть реализована на соответствующей машине Тьюринга (МТ). В ходе развития теории алгоритмов появился целый ряд модификаций МТ, одна из наиболее распространенных версий которой была предложена Постом. Эту версию МТ обычно представляют в виде автоматически функционирующего устройства, включающего в себя следующие основные части: 1) внешний алфавит, т.е. конечное множество символов 2) внутренний алфавит машины 3) бесконечную в обе стороны ленту, представляющую собой внешнюю память машины. Эта лента разбита на клетки. В каждую клетку может быть записана только одна буква алфавита. Пустую клетку обозначают символом

Перед началом работы машины на ленту записывается исходная информация, а управляющая головка устанавливается, как правило, у крайнего левого символа входного слова с указанием начального состояния
1. После конечного числа тактов машина останавливается, переходя в стоп-состояние 2. Машина никогда не останавливается, т.е. не переходит в стоп-состояние В каждом такте МТ работает по функциональной схеме, которую условно можно представить так:
где В зависимости от того, какая буква на ленте обозревается (считывается) управляющей головкой (в приведенном выше случае буква 1) буквы внешнего алфавита 2) адреса внешней памяти п, л, н; 3) нового состояния машины Совокупность всех команд, которые могут формироваться в каждом такте, образует программу МТ. Эта программа представляется двумерной таблицей и называется Тьюринговой функциональной схемой (табл. 10).
Таблица 10
Для простоты изображения различных конфигураций, получаемых в результате работы МТ, будем в дальнейшем записывать информацию в виде слова, не изображая самой ленты и ее разбивки на клетки. Не будем также изображать управляющую головку, а будем записывать лишь состояние машины. Рассмотрим пример работы МТ, функциональная схема которой задана табл.10, а начальная конфигурация имеет вид a 0 a 2 a 2 a 0. q 1 Так как управляющей головкой обозревается буква a 2 и машина находится в состоянии q 1 то ею будет выработана команда a 2л q 1 которая находится в табл.10 на пересечении строки q 1 и столбца a 2 В соответствии с этой командой обозреваемая буква внешнего алфавита a 2 заменяется на ту же самую букву a 2 т.е. не изменяется, а состояние машины q 1 заменяется на q 1 т.е. тоже не изменяется, но происходит сдвиг управляющей головки влево вдоль ленты на одну клетку. В результате получим новую конфигурацию a 0 a 2 a 2 a 0. q 1 В этой конфигурации обозреваемая буква a 2 и состояние машины q 1 не изменились. Поэтому этой конфигурации соответствует та же команда, и мы сдвигаемся на одну клетку влево и получаем конфигурацию a 0 a 2 a 2 a 0. q 1 Пустой клетке a 0 и состоянию q 1 соответствует команда a 2л q 3 из табл.10. В соответствии с этой командой обозреваемая буква a 0 (пустая клетка) должна замениться на букву a 2, а состояние машины q 1 – на состояние q 3. С учетом этого и с учетом необходимости сдвига головки влево на одну клетку, получим конфигурацию a 0 a 2 a 2 a 2 a 0. q 3 Этой конфигурации соответствует команда a 0п q 0, выполняя которую, получим следующую конфигурацию: a 0 a 2 a 2 a 2 a 0. q 0 Так как в случае последней конфигурации машина попала в состояние q 0 (стоп-состояние), то процесс останавливается и слово a 2 a 2 a 2, заключенное между двумя пустыми клетками (слева a 0 и справа a 0), является результатом работы машины. Поскольку исходным словом было a 2 a 2, то произошло преобразование его машиной Тьюринга в слово a 2 a 2 a 2. Рассмотрим случай, когда процесс будет повторяться бесконечно долго. Пусть функциональная схема задается той же табл.10, а исходная конфигурация имеет вид a 0 a 1 a 2 a 2 a 0. q 1 Так как управляющей головкой обозревается буква a 2 а машина находится в состоянии q 1, то в соответствии с табл.10 машиной будет выработана команда a 2л q 1. Поэтому управляющая головка сдвинется влево на одну клетку, буква a 2 заменится на a 2 (т.е. останется без изменения), состояние q 1 также не изменится и следующая (вторая) конфигурация будет иметь вид a |

 найдется такой номер шага
найдется такой номер шага  , что на этом шаге ошибка в определении решения задачи не превысит
, что на этом шаге ошибка в определении решения задачи не превысит  .
.
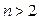 уравнение
уравнение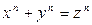
 .
. . В частном случае для
. В частном случае для  доказана противоположная теорема (т.е. что решение существует) и известны даже два ее эквивалентных решения:
доказана противоположная теорема (т.е. что решение существует) и известны даже два ее эквивалентных решения:  где
где  – это первое решение;
– это первое решение; 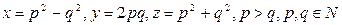 − это второе решение.
− это второе решение. значений ее аргумента и область
значений ее аргумента и область 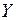 значений функций, каждому из которых сопоставлено некотороезначение аргумента, совпадают. Исследования показали, что совокупность частично вычислимых функций для самых разных пониманий алгоритма оказывается одной и той же. Все частичные функции, алгоритмы вычисления которых известны, оказались частично-рекурсивными (от лат. recursio – возвращение). Частично-рекурсивные функции – это функции, определяемые особым образом с достаточной математической строгостью. А именно: если функция может быть получена за конечное число шагов из некоторых простейших функций с помощью операций суперпозиции, примитивной рекурсии и операции минимизации. Упомянутые простейшие функции и операции мы подробнее рассмотрим ниже.
значений функций, каждому из которых сопоставлено некотороезначение аргумента, совпадают. Исследования показали, что совокупность частично вычислимых функций для самых разных пониманий алгоритма оказывается одной и той же. Все частичные функции, алгоритмы вычисления которых известны, оказались частично-рекурсивными (от лат. recursio – возвращение). Частично-рекурсивные функции – это функции, определяемые особым образом с достаточной математической строгостью. А именно: если функция может быть получена за конечное число шагов из некоторых простейших функций с помощью операций суперпозиции, примитивной рекурсии и операции минимизации. Упомянутые простейшие функции и операции мы подробнее рассмотрим ниже. ;
; ;
; .
. и
и  . Рассмотрим функцию
. Рассмотрим функцию  , определяемую равенством
, определяемую равенством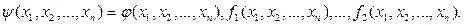
 получена из функций
получена из функций  и
и  их суперпозицией.
их суперпозицией.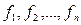 и
и  , при которых функция
, при которых функция  не всюду определена.
не всюду определена. и
и  . Запишем функцию
. Запишем функцию 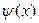 в виде
в виде  Пусть
Пусть 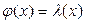 , а
, а 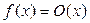 тогда
тогда  Пусть
Пусть  , а
, а  . Пусть функция
. Пусть функция 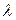 связывает функции
связывает функции 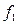 и
и  как функцию от функции, тогда будем иметь
как функцию от функции, тогда будем иметь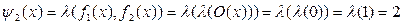 .
. и
и  тоже будут всюду определенными интуитивно вычислимыми.
тоже будут всюду определенными интуитивно вычислимыми. и
и  . Из этих функций составим новую функцию, удовлетворяющую следующим равенствам:
. Из этих функций составим новую функцию, удовлетворяющую следующим равенствам: (1)
(1) аргумента, функция
аргумента, функция  − от
− от  аргументов, а функция
аргументов, а функция  аргумента. Говорят, что если функция
аргумента. Говорят, что если функция  получена из функций
получена из функций  . Тогда последовательно находим
. Тогда последовательно находим ;
;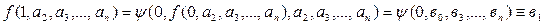 ;
;
 , то СПР будет иметь вид
, то СПР будет иметь вид (2)
(2) , (3)
, (3) , и
, и  с помощью операции суперпозиции, СПР и операции минимизации. Если же функция получается из тех же простейших функций,
с помощью операции суперпозиции, СПР и операции минимизации. Если же функция получается из тех же простейших функций, 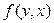 , так и
, так и  (4)
(4) Но второе равенство системы (4) еще не дает основания считать, что система этих двух равенств представляет СПР, поскольку по определению правая часть второго равенства должна зависеть от трех (в данном случае) аргументов. Поэтому левую часть второго равенства, зависящую от двух аргументов
Но второе равенство системы (4) еще не дает основания считать, что система этих двух равенств представляет СПР, поскольку по определению правая часть второго равенства должна зависеть от трех (в данном случае) аргументов. Поэтому левую часть второго равенства, зависящую от двух аргументов  , приведем к виду, зависящему от трех аргументов
, приведем к виду, зависящему от трех аргументов  , т.е. нам надо получить
, т.е. нам надо получить  в явном виде.
в явном виде. , тогда на основании второго равенства нашей системы будем иметь
, тогда на основании второго равенства нашей системы будем иметь  . Сделаем замену
. Сделаем замену  , тогда
, тогда  но функцию
но функцию  от двух аргументов мы можем обозначить любой дугой буквой, например,
от двух аргументов мы можем обозначить любой дугой буквой, например, 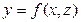 . Тогда получим
. Тогда получим  .
. заданную двумя равенствами, мы свели к СПР, заданной также двумя равенствами:
заданную двумя равенствами, мы свели к СПР, заданной также двумя равенствами: (5)
(5) , используя полученную СПР соответствующее число раз (фактически используя алгоритм в строгом смысле его понимания).
, используя полученную СПР соответствующее число раз (фактически используя алгоритм в строгом смысле его понимания).
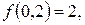 последовательно можно записать:
последовательно можно записать: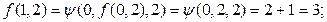




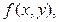 соответствующей СПР (5). Для этого воспользуемся сначала вторым равенством системы (5) и последовательно запишем
соответствующей СПР (5). Для этого воспользуемся сначала вторым равенством системы (5) и последовательно запишем
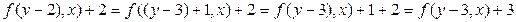 .
.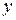 раз, мы придем в конце концов к выражению
раз, мы придем в конце концов к выражению 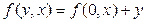 . Но учитывая первое равенство системы (4)
. Но учитывая первое равенство системы (4)  , окончательно будем иметь
, окончательно будем иметь  . Отсюда видим, что обычную операцию сложения можно свести к алгоритмическому процессу (к схеме примитивной рекурсии) вычисления суммы двух чисел. Действительно, используя СПР в рассматриваемом примере, мы получили
. Отсюда видим, что обычную операцию сложения можно свести к алгоритмическому процессу (к схеме примитивной рекурсии) вычисления суммы двух чисел. Действительно, используя СПР в рассматриваемом примере, мы получили  . То же самое мы получим из аналитического выражения при тех же численных значениях аргументов
. То же самое мы получим из аналитического выражения при тех же численных значениях аргументов  .
. . Зафиксируем значение
. Зафиксируем значение  и найдем значение
и найдем значение 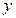 , при котором
, при котором  . В частном случае может
. В частном случае может  . Сложнее решается задача отыскания для данной функции
. Сложнее решается задача отыскания для данной функции 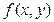 и фиксированного
и фиксированного  наименьшего из тех значений
наименьшего из тех значений  при котором
при котором  поэтому наименьшее значение y, при котором
поэтому наименьшее значение y, при котором  . Эту функцию принято обозначать
. Эту функцию принято обозначать  , и при этом говорят, что для перехода от функции
, и при этом говорят, что для перехода от функции  к функции
к функции 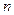 переменных μ - оператор определяется аналогично
переменных μ - оператор определяется аналогично .
.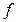 путем применения μ -оператора можно по следующему алгоритму.
путем применения μ -оператора можно по следующему алгоритму. . Если
. Если  , то полагаем
, то полагаем  . Если
. Если 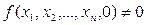 , то увеличиваем
, то увеличиваем  . Если
. Если  , то полагаем
, то полагаем  . Если же
. Если же  , то увеличиваем
, то увеличиваем  . Найденное значение
. Найденное значение  , и процесс будет продолжаться бесконечно долго. В этом случае считают функцию
, и процесс будет продолжаться бесконечно долго. В этом случае считают функцию 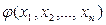 неопределенной. Возможны и другие случаи, когда процесс будет продолжаться бесконечно долго. Это будет тогда, когда значение функции
неопределенной. Возможны и другие случаи, когда процесс будет продолжаться бесконечно долго. Это будет тогда, когда значение функции 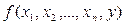 для
для 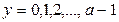 определены, но отличны от
определены, но отличны от  , а значение
, а значение  не определено.
не определено. представим с помощью μ -оператора:
представим с помощью μ -оператора: 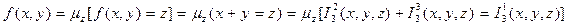 . Пользуясь представлением функции
. Пользуясь представлением функции  , т.е. найдем то значение
, т.е. найдем то значение  при котором
при котором  . Для этого, зафиксировав
. Для этого, зафиксировав  , будем последовательно изменять значения
, будем последовательно изменять значения 




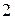
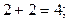




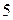


 задана равенствами
задана равенствами
 ; найти аналитический вид функции
; найти аналитический вид функции  сведя ее к СПР.
сведя ее к СПР. свести к СПР и вычислить по ней
свести к СПР и вычислить по ней  .
.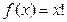 в виде СПР и вычислить по ней
в виде СПР и вычислить по ней  .
. . Вычислить с помощью этой СПР значение
. Вычислить с помощью этой СПР значение  .
.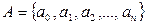 , с помощью которого входная информация кодируется в виде некоторой последовательности букв этого алфавита (слов) и вводится в машину. Последняя перерабатывает информацию, представленную в виде слова, в новое слово;
, с помощью которого входная информация кодируется в виде некоторой последовательности букв этого алфавита (слов) и вводится в машину. Последняя перерабатывает информацию, представленную в виде слова, в новое слово; . Символы
. Символы  определяют конечное число состояний машины, причем два состояния имеют особое значение:
определяют конечное число состояний машины, причем два состояния имеют особое значение:  − начальное состояние,
− начальное состояние, 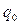 − конечное состояние (стоп-состояние). Символы п, л, н − это соответственно символы сдвига (вправо, влево, на месте).
− конечное состояние (стоп-состояние). Символы п, л, н − это соответственно символы сдвига (вправо, влево, на месте). .
. , как показано на рис.1 (это состояние машины называют начальной конфигурацией).
, как показано на рис.1 (это состояние машины называют начальной конфигурацией). , так как может преобразовать ее в результирующую информацию
, так как может преобразовать ее в результирующую информацию  .
. ,
, п, л, н − символы сдвига.
п, л, н − символы сдвига. ) и в каком состоянии (в приведенном случае
) и в каком состоянии (в приведенном случае  ) находится машина, в каждом такте вырабатывается команда, определяющая поведение машины в следующем такте и состоящая из трех элементов:
) находится машина, в каждом такте вырабатывается команда, определяющая поведение машины в следующем такте и состоящая из трех элементов: , на которую заменяется обозреваемая буква
, на которую заменяется обозреваемая буква  .
. a 2л q 3
a 2л q 3



