
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формальное представление алгоритма. Машина ТьюрингаСодержание книги
Поиск на нашем сайте Тьюринг дал четкое определение понятия метода. Отталкиваясь от интуитивного представления о методе как о некоем алгоритме, т.е. процедуре, которая может быть выполнена механически, без творческого вмешательства, он показал, как эту идею можно воплотить в виде подробной модели вычислительного процесса. Полученная модель вычислений, в которой каждый алгоритм разбивался на последовательность простых, элементарных шагов, и была логической конструкцией, названной впоследствии машиной Тьюринга. Машину Тьюринга можно представить следующим образом. Это есть автоматически работающее устройство, способное находиться в конечном числе состояний. Среди ее состояний имеются два выделенных – начальное и конечное. Процесс функционирования осуществляется по шагам. Во время каждого из них машина Тьюринга переходит из одного состояния в какое-то другое, причем это другое состояние, в частности, может совпадать с предыдущим. Процесс начинается с начального состояния и заканчивается конечным. Вся информация, необходимая для реализации алгоритма, хранится в памяти. Память представляет бесконечную в обе стороны ленту, разделенную на клетки. В каждой клетке ленты может быть записана какая-то одна буква из некоторого алфавита. Если в клетке ничего не записано, то считается, что в ней записана «пустая» буква. В машине Тьюринга имеется комбинированная головка считывания-записи информации. Условно можно считать, что головка расположена над лентой. Процесс считывания-записи осуществляется последовательно по одной букве за один шаг. Во время считывания-записи головка находится над одной клеткой ленты. При реализации каждого шага функционирования машины Тьюринга происходит следующее. Предположим, что головка считывания-записи расположена над какой-то клеткой, и машина Тьюринга находится в одном из своих состояний, отличном от конечного. Тогда в зависимости от состояния машины Тьюринга и буквы, записанной в клетке, осуществляется запись некоторой буквы в эту же клетку, а сама машина Тьюринга переходит в новое состояние. Вновь записанная буква, в частности, может совпадать с буквой, бывшей в клетке перед записью. После этого лента передвигается на одну клетку вправо или влево, или остается на месте. Как только машина Тьюринга переходит в конечное состояние, процесс останавливается. Перечисление всех возможных шагов машины Тьюринга называется программой. Программа является точно описанным объектом. Вообще говоря, ее содержание зависит от используемого алфавита. Конкретное описание машины Тьюринга может в деталях отличаться от рассмотренного. Например, память может представлять ленту, бесконечную только в одну сторону, в машине могут выделяться некоторые другие устройства, такие как исполнительное, лентопротяжное и т.п., можно допустить наличие нескольких головок считывания-записи со своими лентами и многое другое. Однако в любом случае процесс функционирования машины Тьюринга будет описываться некоторой программой. Так как машины Тьюринга достаточно адекватно отражают интуитивное понятие алгоритма, то это означает, что изучение структуры алгоритмов неизбежно связано с изучением структуры описывающих алгоритмы программ. Формально машина Тьюринга может быть описана следующим образом: Пусть заданы · Конечное множество состояний · Конечное множество символов ленты · Функция · Существует выделенный пустой символ · Подмножество · Одно из состояний Решаемая проблема задается путем записи на ленту конечного количества символов
После задания проблемы машина переводится в начальное состояние, и головка устанавливается у самого левого непустого символа, после чего в соответствии с указанной функцией переходов Алгоритмы, реально используемые на практике, очень редко записываются в виде программ для машины Тьюринга. Но машина Тьюринга имеет чрезвычайно важное значение в силу следующего. Тьюринг высказал предположение, что любой алгоритм в интуитивном смысле этого слова может быть представлен эквивалентной машиной в предложенной им модели вычислений. Это предположение известно как тезис Черча-Тьюринга. Каждый компьютер может моделировать машину Тьюринга, для этого достаточно моделировать операции перезаписи ячеек, сравнения и перехода к другой соседней ячейке с учетом изменения состояния машины. Таким образом, он может моделировать алгоритмы в машине Тьюринга, и из этого тезиса следует, что все компьютеры, независимо от мощности, архитектуры и других особенностей, эквивалентны с точки зрения принципиальной возможности решения алгоритмически разрешимых задач.
4. Алгоритмически неразрешимые проблемы: их существование и примеры Существуют ли какие-нибудь проблемы, для которых невозможно придумать алгоритмы их решения? Утверждение о существовании алгоритмически неразрешимых проблем является весьма сильным – мы констатируем, что мы не только сейчас не знаем соответствующего алгоритма, но мы не сможем никогда принципиально его найти. Сегодня при доказательстве алгоритмической неразрешимости некоторой задачи принято сводить ее к ставшей классической задаче – «задаче останова» машины Тьюринга. Имеет место следующая теорема [Макконнелл]. Теорема. Не существует алгоритма (машины Тьюринга), позволяющего по описанию произвольного алгоритма и его исходных данных, при этом и алгоритм и данные заданы символами на ленте машины Тьюринга, определить, останавливается ли этот алгоритм на этих данных или работает бесконечно. Таким образом, фундаметально алгоритмическая неразрешимость связана с бесконечностью выполняемых алгоритмом действий. Примеры алгоритмически неразрешимых проблем. Пример 1. Распределение девяток в записи числа Поскольку число Пример 2. Вычисление совершенных чисел. Совершенные числа – это числа, которые равны сумме своих делителей, за исключением самого числа, например: 28=1+2+4+7+14. Определим функцию Пример 3. Десятая проблема Гильберта. Пусть задан Пример 4. Проблема останова машины Тьюринга. Пример 5. Проблема эквивалентности алгоритмов. По двум произвольным заданным алгоритмам, например, по двум машинам Тьюринга, определить, будут ли они выдавать одинаковые выходные результаты для любых входных данных. Пример 6. Проблема тотальности. По записи произвольного заданного алгоритма определить, будет ли он останавливаться на всех возможных наборах исходных данных. Другая формулировка этой задачи: является ли частичный алгоритм А всюду определенным алгоритмом? В теории алгоритмов проблемы, для которых может быть предложен частичный алгоритм их решения, частичный в том смысле, что он возможно, но не обязательно, за конечное количество шагов находит решение проблемы, называются частично разрешимыми проблемами. Например, проблема останова является частично разрешимой проблемой, а проблема эквивалентности и тотальности не являются таковыми.
Вопросы 1. Интуитивные определения понятия алгоритма, их недостатки. 2. Определения алгоритма по Колмогорову, по Маркову. Сравнение этих определений. 3. Общие требования к алгоритму, не зависящие от используемого определения алгоритма. 4. В чем заключается требование конечности записи алгоритма? 5. В чем заключается требование конечности действий алгоритма? 6. В чем заключаются требования универсальности и правильности алгоритма? 7. Постройте алгоритм получения положительной оценки на экзамене. 8. Постройте алгоритм для процесса завязывания шнурков, проверте его работу на своем коллеге. 9. Для чего служит машина Тьюринга? 10. Что представляет из себя алгоритмически неразрешимая проблема? 11. Является ли алгоритмически неразрешимой проблема решения уравнения:
Література 1. Дж. Макконнелл. Основы современных алгоритмов. 2-е дополненное издание. – М.: Техносфера, 2004. – 368 с. 2. Воеводин В.В. Параллельные вычисления / В.В.Воеводин, Вл.В.Воеводин. — СПб.: БХВ-Петербург, 2002. — 608 с.
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1873; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 , в которых может находиться машина Тьюринга;
, в которых может находиться машина Тьюринга; ;
; (функция переходов или программа), которая задается отображением пары из декартова произведения
(функция переходов или программа), которая задается отображением пары из декартова произведения  (например, машина находится в состоянии
(например, машина находится в состоянии  и обозревает символ
и обозревает символ  ) в тройку из произведения
) в тройку из произведения 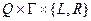 (машина переходит в состояние
(машина переходит в состояние  , заменяет символ
, заменяет символ  и пердвигается влево или вправо на одну ячейку ленты), т.е.
и пердвигается влево или вправо на одну ячейку ленты), т.е. 
 ;
; - входной алфавит,
- входной алфавит,  , определяется как подмножество входных символов ленты, причем
, определяется как подмножество входных символов ленты, причем 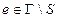 ;
; является начальным состоянием машины.
является начальным состоянием машины. образующих слово
образующих слово  в алфавите
в алфавите  .
.
 машина начинает заменять обозреваемые символы, передвигать головку вправо или влево и переходить в другие состояния. Останов машины происходит в том случае, если для пары
машина начинает заменять обозреваемые символы, передвигать головку вправо или влево и переходить в другие состояния. Останов машины происходит в том случае, если для пары  функция перехода неопределена.
функция перехода неопределена. . Определим функцию
. Определим функцию  , где
, где  - количество девяток подряд в десятичной записи числа
- количество девяток подряд в десятичной записи числа  - номер самой левой после запятой девятки из
- номер самой левой после запятой девятки из 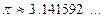 , то
, то  . Задача состоит в вычислении функции
. Задача состоит в вычислении функции  для произвольного
для произвольного  =
=  - многочлен степени
- многочлен степени  решение в целых числах. Ю.В.Матиясевич показал, что такого алгоритма не существует, т.е. отсутствует общий метод определения целых корней уравнения
решение в целых числах. Ю.В.Матиясевич показал, что такого алгоритма не существует, т.е. отсутствует общий метод определения целых корней уравнения  , где
, где  – многочлен степени n? Почему?
– многочлен степени n? Почему?


