
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Змістовий модуль 1. Поняття алгоритму. Особливості чисельних алгоритмівСодержание книги
Поиск на нашем сайте Передмова Предметом вивчення в курсі «Аналіз та розпаралелювання алгоритмів» є алгоритми, їх структура та властивості.
Мета: Одержання загальної інформації про алгоритми, їх властивості та структуру, формування навичок і вмінь проведення аналізу властивостей алгоритмів, їх порівняння, побудови різноманітних методів для формування алгоритмів з заданими характеристиками.
Місце дисципліни у навчальному процесі: у системі підготовки магістрів за спеціальністю – «Інформатика» дисципліна “Аналіз та розпаралелювання алгоритмів ” є фундаментальною.
Задачі вивчення дисципліни: 1. Формування у студентів загального поняття алгоритму, використання його для можливості порівняння декількох алгоритмів за різними параметрами; 2. Формування навичок виділяти головні характеристики алгоритмів; 3. Формування навичок аналізувати алгоритм на основі його графу; 4. Формування навичок виявлення наявності (відсутності) внутрішнього паралелизму алгоритму для з’ясування питання про можливість його розпаралелювання; 5. Формування навичок аналізувати алгоритм на основі його часових розгорток.
Структура дисципліни: · Кількість кредитів – 4 · Кількість семестрових модулів – 2 · Повний обсяг часу на вивчення дисципліни, в годинах – 144 · В тому числі аудиторні заняття, в годинах – 46 · З них: лекційні, в годинах – 30 лабораторні, в годинах – 16 · Обсяг часу на самостійну роботу студента, у годинах – 98 · Підсумкова форма рейтингового контролю – іспит Семестровий модуль 1. Змістовий модуль 1. ПОНЯТТЯ АЛГОРИТМУ. ОСОБЛИВОСТІ ЧИСЕЛЬНИХ АЛГОРИТМІВ Лекция 1. ФОРМАЛИЗАЦИЯ ПОНЯТИЯ АЛГОРИТМА План
Вопросы 1. Интуитивные определения понятия алгоритма, их недостатки. 2. Определения алгоритма по Колмогорову, по Маркову. Сравнение этих определений. 3. Общие требования к алгоритму, не зависящие от используемого определения алгоритма. 4. В чем заключается требование конечности записи алгоритма? 5. В чем заключается требование конечности действий алгоритма? 6. В чем заключаются требования универсальности и правильности алгоритма? 7. Постройте алгоритм получения положительной оценки на экзамене. 8. Постройте алгоритм для процесса завязывания шнурков, проверте его работу на своем коллеге. 9. Для чего служит машина Тьюринга? 10. Что представляет из себя алгоритмически неразрешимая проблема? 11. Является ли алгоритмически неразрешимой проблема решения уравнения:
Література 1. Дж. Макконнелл. Основы современных алгоритмов. 2-е дополненное издание. – М.: Техносфера, 2004. – 368 с. 2. Воеводин В.В. Параллельные вычисления / В.В.Воеводин, Вл.В.Воеводин. — СПб.: БХВ-Петербург, 2002. — 608 с.
Лекция 2. Численные алгоритмы и их характеристики. План
Вопросы
Литература
2. Кобозєва А.А., Мачалін І.О., Хорошко В.О. Аналіз захищеності інформаційних систем. - К.: Вид. ДУІКТ, 2010. – 316 с. 3. Кобозева А.А., Хорошко В.А. Анализ информационной безопасности. - К.: Изд.ГУИКТ, 2009. – 251 с. 4. Деммель Дж. Вычислительная линейная алгебра / Дж.Деммель; пер.с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 430 с. 5. Бахвалов Н.С. Численные методы / Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. — М.: БИНОМ. Лаборатория знаний, 2006. — 636 с. 6. Каханер Д. Численные методы и программное обеспечение / Д.Каханер, К.Моулер, С.Нэш; пер. с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 575 с. 7. E.Anderson, Z.Bai, C.Bischof, J.Demmel, J.Dongarra, J.Du Croz, A.Greenbaum, S.Hammarling, A.McKenney, S.Ostrouchov, and D.Sorensen. LAPACK Users’ Guide (2nd edition). SIAM, Philadelphia,PA, 1995.
Змістовий модуль 2. ОСНОВЫ АНАЛИЗА АЛГОРИТМОВ План
Классы входных данных Роль входных данных в анализе алгоритмов чрезвычайно велика, поскольку последовательность действий алгоритма определяется не в последнюю очередь входными данными. Например, чтобы найти наибольший элемент в списке из
Если список изначально упорядочен в порядке убывания, то перед началом цикла будет сделано одно присваивание, а в теле цикла присваиваний не будет вообще. Если список первоначально упорядочен по возрастанию, то всего будет сделано Как только выделены классы, просматривается поведение алгоритма на одном множестве из каждого класса. Если классы выбраны правильно, то на всех множествах входных данных одного класса алгоритм производит одинаковое количество операций, а на множествах из другого класса это количество, в общем случае, будет другим.
Вопросы 1. Какие основные характеристики алгоритма оцениваются при его анализе? 2. Как целесообразно оценивать «время» выполнения алгоритма? Почему? Что такое вычислительная сложность алгоритма? 3. В каких случаях сравнивается эффективность работы разных алгоритмов? 4. Должен ли анализ алгоритма учитывать особенности компьютера, на котором этот алгоритм реализован? Почему? 5. Влияют ли входные данные задачи на последовательность действий алгоритма? Привести пример. 6. Что представляют из себя классы входных данных? 7. Насколько значимым в настоящее время является вопрос используемой алгоритмом памяти? Литература 1. Дж. Макконнелл. Основы современных алгоритмов. 2-е дополненное издание. – М.: Техносфера, 2004. – 368 с. 2. Гуц А.К. Математическая логика и теория алгоритмов: Учебное пособие. – Омск: Изд-во Наследие. Диалог-Сибирь, 2003. – 108 с. 3. Деммель Дж. Вычислительная линейная алгебра / Дж.Деммель; пер.с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 430 с. 4. Бахвалов Н.С. Численные методы / Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. — М.: БИНОМ. Лаборатория знаний, 2006. — 636 с. 5. Каханер Д. Численные методы и программное обеспечение / Д.Каханер, К.Моулер, С.Нэш; пер. с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 575 с.
План Предварительные шаги для оценки вычислительной сложности алгоритма Скорость роста алгоритма Предварительные шаги для оценки вычислительной сложности алгоритма Подсчет вычислительной сложности алгоритма состоит из двух основных шагов: Шаг 1. Выбор значимой операции или группы операций. Шаг 2. Определение, какие из выбранных операций содержатся в теле алгоритма, а какие составляют накладные расходы или уходят на регистрацию и учет данных. В качестве значимых часто (но не обязательно) выступают операции двух типов:
Арифметические операции разбиваются на две группы:
Аддитивные операторы (сложения) включают сложение, вычитание, увеличение и уменьшение счетчика. Мультипликативные операторы (умножения) включают умножение, деление, взятие остатка по модулю. Разбиение на эти две группы связано с тем, что умножения работают дольше, чем сложения. На практике некоторые алгоритмы считаются предпочтительнее других, если в них меньше умножений, даже если число сложений при этом пропорционально возрастает. Поскольку при анализе алгоритма выбор входных данных может существенно повлиять на его выполнение, желательно найти такие данные, которые обеспечивают как самое быстрое, так и самое медленное выполнение алгоритма, а также оценить среднюю эффективность алгоритма на всех возможных наборах данных. Очень часто при анализе алгоритма оценивается лишь наихудший (самый медленный) вариант.
Скорость роста алгоритма Точное значение количества операций, выполненных алгоритмом, не играет существенной роли в его анализе. Более важной оказывается скорость роста этого числа при возрастании объема входных данных. Она называется скоростью роста алгоритма. Именно эта характеристика часто и фигурирует как оценка вычислительной сложности алгоритма. Существенным является общий характер поведения алгоритмов, а не подробности этого поведения. Предположим, что количество операций четырех различных алгоритмов определяется в соответствии с функциями
где – Если рассмотреть графики этих функций (рис.4.1)
Рис. 4.1.
например, на промежутке от 1 до 35, то становится очевидным, что несмотря на то, что функция Таким образом, при анализе алгоритмов существенным является поведении функции зависимости количества операций от размера входных данных Некоторые часто встречающиеся функции приведены в таблице 4.1. Очевидно, что при небольших размерах входных данных значения функций отличаются незначительно, при росте этих размеров разница существенно возрастает. Поэтому существенным является поведение функции на больших объемах входных данных, поскольку на малых объемах принципиальная разница оказывается скрытой. Таблица 4.1-
Для иллюстрации последующего вывода рассмотрим пример функции, которая трактуется как закон зависимости количества арифметических операций некоторого гипотетического алгоритма от размера входных данных
Предложенная функция является суммой нескольких функций, скорость возрастания которых различна. Очевидно, что скорость роста всей Определение. Говорят, что функции
(читается: функция
Рассмотрим другой пример:
Ясно, что скорость возрастания
Из чего вытекает, что
Отбрасывая все младшие члены, скорость роста которых меньше, получаем порядок вычислительной сложности алгоритма [Макконнелл]. В предыдущем рассмотренном примере поскольку
Вопросы 1. Какие предварительные шаги предпринимаются для оценки вычислительной сложности алгоритма? 2. На какие две группы разбиваются арифметические операции? Почему? 3. Какие наборы данных желательно найти при оценке вычислительной сложности алгоритма? 4. Что называется скоростью роста алгоритма? 5. Что такое порядок вычислительной сложности алгоритма? Как он оценивается? 6. Что представляет из себя последовательный поиск информации, двоичный поиск, выборка? Литература 1. Дж. Макконнелл. Основы современных алгоритмов. 2-е дополненное издание. – М.: Техносфера, 2004. – 368 с. 2. Гуц А.К. Математическая логика и теория алгоритмов: Учебное пособие. – Омск: Изд-во Наследие. Диалог-Сибирь, 2003. – 108 с. 3. Деммель Дж. Вычислительная линейная алгебра / Дж.Деммель; пер.с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 430 с. 4. Бахвалов Н.С. Численные методы / Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. — М.: БИНОМ. Лаборатория знаний, 2006. — 636 с. 5. Каханер Д. Численные методы и программное обеспечение / Д.Каханер, К.Моулер, С.Нэш; пер. с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 575 с.
Лекция 5. Сложностные классы задач План 1. Класс Р - задачи с полиномиальной сложностью Вопросы 1. Какая задача называется полиномиальной? Привести примеры алгоритмов, имеющих полиномиальную сложность. 2. Чем отличается полиномиальная задача от полиномиального алгоритма? 3. Какая задача содержательно относится к классу NP? Привести примеры таких задач. 4. В чем суть задачи о коммивояжере? 5. Сформулировать задачу о раскраске графа. 6. В чем заключается задача об упаковке рюкзака?
Литература 1. Дж. Макконнелл. Основы современных алгоритмов. 2-е дополненное издание. – М.: Техносфера, 2004. – 368 с. 2. Гуц А.К. Математическая логика и теория алгоритмов: Учебное пособие. – Омск: Изд-во Наследие. Диалог-Сибирь, 2003. – 108 с. 3. Деммель Дж. Вычислительная линейная алгебра / Дж.Деммель; пер.с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 430 с. 4. Бахвалов Н.С. Численные методы / Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. — М.: БИНОМ. Лаборатория знаний, 2006. — 636 с. 5. Каханер Д. Численные методы и программное обеспечение / Д.Каханер, К.Моулер, С.Нэш; пер. с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 575 с. Лекция 6. Сложностные классы задач (продолжение) План 1. Проблема Р=NP Вопросы 1. В чем заключается основная проблема теории сложности? 2. Понятие NP -полноты. 3. Жадные алгоритмы, их основная идея. Примеры жадных алгоритмов.
Литература 6. Дж. Макконнелл. Основы современных алгоритмов. 2-е дополненное издание. – М.: Техносфера, 2004. – 368 с. 7. Каханер Д. Численные методы и программное обеспечение / Д.Каханер, К.Моулер, С.Нэш; пер. с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 575 с.
План Вопросы
Литература
4. Воеводин В.В. Вычислительные основы линейной алгебры / В.В.Воеводин. — М.: Наука. Гл.ред.физ.-мат.лит., 1977. — 304 с. Семестровий модуль 2. АНАЛИЗ ПОСЛЕДОВАТЕЛЬНЫХ АЛГОРИТМОВ ДЛЯ ИСПОЛЬЗОВАНИЯ В ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМАХ Лекция 8.Граф информационной зависимости реализации алгоритма – основной способ представления алгоритма для выявления внутреннего параллелизма План Последовательность операций
Очевидно, что графы, отвечающие различным последовательностям операций для рассматриваемого примера (рис.8.1), являются изоморфными.
Рис.8.1
По существу, в (100) фиксирован не один алгоритм, а несколько математически эквивалентных. Пример 20. Исследовать различные способы вычисления суммы
В точной арифметике операция сложения обладает свойством коммутативности и ассоциативности. Очевидно, что общее число различных способов вычисления выражения (150) при больших
которой соответствует граф
соответствующий граф которой:
Можно показать, что схема последовательного суммирования хуже по точности, чем схема сдваивания, примерно, в Замечание. Графы алгоритмов примера 10 и схемы сдваивания примера 20 очевидно являются изоморфными, хотя соответствуют решению совершенно разных задач. Алгоритмы с изоморфными графами обладают многими общими свойствами, по крайней мере, в той части, которая касается распределения информации при реализации алгоритмов (хотя призваны решать возможно совершенно разные задачи). Замечание. Графы алгоритмов примеров 10, 20 имеют достаточно ясную и простую структуру, которая определяется не только самими алгоритмами. Во многом она зависит и от того, как конкретно на плоскости выбраны места расположения вершин. При случайном выборе расположения вершин структуру графа можно не разглядеть. Задачу выбора наилучшего расположения вершин можно пытаться решить, если число вершин невелико. При этом, возможно, придется использовать полный перебор рассматриваемых вариантов. В типичных ситуациях число операций алгоритма огромно, более того, чаще всего оно даже точно не определено и задается какими-нибудь параметрами. В этих случаях использование полного перебора вариантов для решения задачи о построении и исследовании графа алгоритма практически нереально.
3. Допустимые преобразования алгоритма Граф алгоритма не накладывает на порядок выполнения операций никаких ограничений, кроме одного: к моменту начала реализации любой операции должны закончить свое выполнение все те операции, которые поставляют для нее аргументы. Таким образом, граф алгоритма определяет некоторое множество допустимых порядков выполнения операций, показывая, как при этом происходит распространение информации. Утверждение 100. Пусть при выполнении операций ошибки округлений определяются только значениями аргументов операций. Тогда при одних и тех же входных данных все реализации алгоритма, соответствующие одному и тому же графу, дают один и тот же результат, включая всю совокупность ошибок округления, независимо от порядка выполнения операций [Воев]. Доказательство. Разобьем множество вершин графа алгоритма Замечание 100. При реализации алгоритма либо алгоритм в целом, либо отдельные его фрагменты иногда приходится подстраивать под особенности вычислительной техники. Эта подстройка фактически означает преобразование алгоритма. Из утверждения 100 вытекает, что преобразования сохраняют уровень достоверности результатов и, следовательно, являются допустимыми, если эти преобразования сохраняют граф алгоритма.
Вопросы 1. Почему исследования “классических” последовательных алгоритмов для определения возможности их использования в параллельных вычислительных системах остаются актуальными в настоящее время? 2. Что такое внутренний параллелизм алгоритма? Любому ли алгоритму присущ внутренний параллелизм? 3. Что представляет из себя граф информационной зависимости реализации алгоритма? 4. Какие ограничения накладывает граф алгоритма на порядок выполнения операций? 5. Какие преобразования алгоритма сохраняют уровень достоверности его результатов?
Литература 1. Воеводин В.В. Параллельные вычисления / В.В.Воеводин, Вл.В.Воеводин. — СПб.: БХВ-Петербург, 2002. — 608 с. 2. Харари Ф. Теория графов / Ф.Харари; пер.с англ. В.П.Козырева. — М.: Мир, 1973. — 300 с. 3. Уилсон Р. Введение в теорию графов / Р.Уилсон. — М.: Мир, 1977. — 207 с. 4. Кристофидес Н. Теория графов. Алгоритмический подход / Н.Кристофидес. — М.: Мир, 1978. — 432 с. 5. Новиков Ф.А. Дискретная математика для программистов / Ф.А.Новиков. — СПб.: Питер, 2006. — 364 с. 6. Иванов Б.Н. Дискретная математика. Алгоритмы и программы / Б.Н.Иванов. — М.: Лаборатория Базовых Знаний, 2001. — 288с.
Лекция 9. Топологическая сортировка графа План Вопросы 1. Почему любая реализация алгоритма должна порождать определенную сортировку его операций? 2. Какими свойствами обладают группы операций, выделенные при сортировке вершин графа? 3. Почему вершины графа любого алгоритма можно разбить, по крайней мере, на три группы? 4. Какая разметка вершин графа называется топологической сортировкой? 5. Какими основными свойствами обладают топологические сортировки? 6. Что представляет из себя топологический уровень? 7. Какая топологическая сортировка называется обобщенной? Какими свойствами обладает обобщенная топологическая сортировка? 8. Какой граф называется линейно упорядоченным?
Литература 1. Воеводин В.В. Параллельные вычисления / В.В.Воеводин, Вл.В.Воеводин. — СПб.: БХВ-Петербург, 2002. — 608 с. 2. Харари Ф. Теория графов / Ф.Харари; пер.с англ. В.П.Козырева. — М.: Мир, 1973. — 300 с. 3. Уилсон Р. Введение в теорию графов / Р.Уилсон. — М.: Мир, 1977. — 207 с. 4. Кристофидес Н. Теория графов. Алгоритмический подход / Н.Кристофидес. — М.: Мир, 1978. — 432 с. 5. Новиков Ф.А. Дискретная математика для программистов / Ф.А.Новиков. — СПб.: Питер, 2006. — 364 с. 6. Иванов Б.Н. Дискретная математика. Алгоритмы и программы / Б.Н.Иванов. — М.: Лаборатория Базовых Знаний, 2001. — 288с.
План 1. Особенности и рекомендации построения топологических сортировок графов алгоритмов, содержащих условные операции Вопросы 1. Когда возникает семейство «похожих» алгоритмов? 2. Всегда ли можно точно построить граф алгоритма, содержащего условные операции? Почему? 3. Можно ли по имеющейся топологической сортировке графа получить топологические сортировки его подграфов? Как это сделать? Когда возникает такая необходимость? Привести пример. 4. Что назыв ется множеством теряемых ребер графа, когда это множество возникает? Привести примеры. 5. Какие вершины графа называются граничными вершинами? Привести примеры. 6. Написать программу, реализующую алгоритм построения топологической сортировки объединения двух графов по имеющимся топологическим сортировкам этих графов.
Литература 1. Воеводин В.В. Параллельные вычисления / В.В.Воеводин, Вл.В.Воеводин. — СПб.: БХВ-Петербург, 2002. — 608 с. 2. Харари Ф. Теория графов / Ф.Харари; пер.с англ. В.П.Козырева. — М.: Мир, 1973. — 300 с. 3. Уилсон Р. Введение в теорию графов / Р.Уилсон. — М.: Мир, 1977. — 207 с. 4. Кристофидес Н. Теория графов. Алгоритмический подход / Н.Кристофидес. — М.: Мир, 1978. — 432 с. 5. Новиков Ф.А. Дискретная математика для программистов / Ф.А.Новиков. — СПб.: Питер, 2006. — 364 с. 6. Иванов Б.Н. Дискретная математика. Алгоритмы и программы / Б.Н.Иванов. — М.: Лаборатория Базовых Знаний, 2001. — 288с. 7. Кобозева А.А., Нариманова Е.В. Метод построения топологической сортировки объединения графов, используемый при распараллеливании последовательных алгоритмов / Труды Одесского политехнического университета. – 2006. - №2(26). - С. 156-161.
Лекция 11. Использование операций гомоморфизма при построении топологических сортировок графов План Вопросы 1. Какая операция над графом называется операцией элементарного гомоморфизма? 2. К каким последствиям в ациклическом графе может привести операция элементарного гомоморфизма? 3. Какая операция над графом называется простым элементарным гомоморфизмом,кратным элементарным гомоморфизмом? 4. Что называется гомоморфной сверткой графа,простой (кратной) гомоморфной сверткой? 5. Какие два графа называются гомоморфными? 6. Что такое гомоморфный образ, прообраз графа? 7. Как связаны между собой топологические сортировки графа и его гомоморфной свертки? 8. Каким образом гомоморфная свертка помогает упрощению процесса исследования структуры алгоритма? Литература 7. Воеводин В.В. Параллельные вычисления / В.В.Воеводин, Вл.В.Воеводин. — СПб.: БХВ-Петербург, 2002. — 608 с. 8. Харари Ф. Теория графов / Ф.Харари; пер.с англ. В.П.Козырева. — М.: Мир, 1973. — 300 с. 9. Уилсон Р. Введение в теорию графов / Р.Уилсон. — М.: Мир, 1977. — 207 с. 10. Кристофидес Н. Теория графов. Алгоритмический подход / Н.Кристофидес. — М.: Мир, 1978. — 432 с. 11. Новиков Ф.А. Дискретная математика для программистов / Ф.А.Новиков. — СПб.: Питер, 2006. — 364 с. 12. Иванов Б.Н. Дискретная математика. Алгоритмы и программы / Б.Н.Иванов. — М.: Лаборатория Базовых Знаний, 2001. — 288с.
План Вопросы 1. Что называется внутренним параллелизмом алгоритма? 2. Достоинства и недостатки использования внутреннего параллелизма алгоритма. 3. Каким образом имеет смысл располагать вершины графа алгоритма в случае, когда алгоритм содержит операторы цикла? Привести пимеры. 4. В чем состоит основной недостаток графа алгоритма при произвольном расположнении и нумерации вершин этого графа?
Литература 1. Воеводин В.В. Параллельные вычисления / В.В.Воеводин, Вл.В.Воеводин. — СПб.: БХВ-Петербург, 2002. — 608 с. 2. Харари Ф. Теория графов / Ф.Харари; пер.с англ. В.П.Козырева. — М.: Мир, 1973. — 300 с. 3. Уилсон Р. Введение в теорию графов / Р.Уилсон. — М.: Мир, 1977. — 207 с. 4. Кристофидес Н. Теория графов. Алгоритмический подход / Н.Кристофидес. — М.: Мир, 1978. — 432 с. 5. Новиков Ф.А. Дискретная математика для программистов / Ф.А.Новиков. — СПб.: Питер, 2006. — 364 с. 6. Иванов Б.Н. Дискретная математика. Алгоритмы и программы / Б.Н.Иванов. — М.: Лаборатория Базовых Знаний, 2001. — 288с. План Время реализации алгоритма Время реализации алгоритма Одной из важнейших характеристик, определяющих эффективность алгоритма, является время его реализации на вычислительной системе. Конечно, это время зависит не только от алгоритма, но и от структуры и временных характеристик вычислительной системы. Алгоритмы, считавшиеся эффективными на однопроцессорных ЭВМ, нередко становятся очень неэффективными на многопроцессорных системах. Как оценивать время реализации алгоритма? Очевидно, что прямое его измерение на конкретной ЭВМ дает возможность сравнивавть временные характеристики различных алгоритмов только по отношению к данной ЭВМ. По отношению к другой ЭВМ аналогичное сравнение, вообще говоря, дает другие результаты. Поэтому необходимо абстрагироваться от вычислительной системы. Для однопроцессорных ЭВМ это происходит за счет сравнения количества арифметических операций. Формально можно считать, что число операций – это время реализации алгоритма на абстрактной однопроцессорной машине, у которой время реализации любой операции равно 1, а время выполнения всех других процедур (ввод-вывод данных, взаимодействие с памятью, передача данных по каналам связи и т.п.) равно 0. При этом предполагается, что операции выполняются подряд без какого-либо простоя в работе ЭВМ. Как было показано на примерах, сравнение времен реализации алгоритмов по числу операций становится неприемлемым, если реализацию алгоритмов проводить на параллельных вычислительных системах. Поэтому и абстрактная последовательная ЭВМ, используемая для сравнения времен реализации алгоритмов, также оказыванется неприемлемой для этой цели. Теперь в качестве подходящей модельной вычислительной системы выступает граф-машина. Есть одно принципиальное отличие между абстрактной последовательной ЭВМ и граф-машиной. Именно, на первой реализуются все алгоритимы, на второй – только один. Будем исследовать множество временных разверток
Вопросы 1. Можно ли любой ориентированный ациклический граф считать графом некоторого алгоритма? Почему? 2. Как должны соотносится между собой время работы алгоритма и время, которое затрачивается на его анализ? 3. В чем состоит основная проблема анализа алгоритмов при помощи соответствующих им графов? 4. Что представляет из себя вектор обобщенной временной развертки, чем он отличается от вектора временной развертки? 5. Что такое вектор реализации алгоритма? Когда вектор реализации нулевой? 6. Как
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 963; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 , где
, где  – многочлен степени n? Почему?
– многочлен степени n? Почему? элементов, можно воспользоваться следующим алгоритмом:
элементов, можно воспользоваться следующим алгоритмом:

 длина массива входных данных.
длина массива входных данных.
 сначала растет медленнее всех рассматриваемых функций, при росте аргумента она увеличивает скорость возрастания быстрее всех остальных, что приводит к тому, что, начиная с некоторого значения аргумента
сначала растет медленнее всех рассматриваемых функций, при росте аргумента она увеличивает скорость возрастания быстрее всех остальных, что приводит к тому, что, начиная с некоторого значения аргумента 
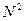


 .
. будет определяться самым быстровозрастающим слагаемым -
будет определяться самым быстровозрастающим слагаемым -  . Иначе говоря, быстрорастущие функции доминируют функции с более медленным ростом, что приводит к тому, что если сложность алгоритма представляет собой сумму двух или нескольких функций, то для оценки алгоритма целесообразно отбрасывать все функции, кроме тех, которые растут быстрее всех.
. Иначе говоря, быстрорастущие функции доминируют функции с более медленным ростом, что приводит к тому, что если сложность алгоритма представляет собой сумму двух или нескольких функций, то для оценки алгоритма целесообразно отбрасывать все функции, кроме тех, которые растут быстрее всех. и
и  связаны соотношением (или сравнимы)
связаны соотношением (или сравнимы)
 .
. .
. , остальными слагаемыми при оценке скорости роста можно пренебречь. Кроме того:
, остальными слагаемыми при оценке скорости роста можно пренебречь. Кроме того: ,
, .
. , то соответствующий гипотетический алгоритм имеет вычислительную сложность порядка
, то соответствующий гипотетический алгоритм имеет вычислительную сложность порядка 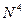 .
.


 . (150)
. (150)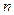 будет очень значительным. Какой способ выбрать? С точки зрения точных вычислений все они эквивалентны. Но в условиях влияния ошибок округления появляются значительные различия. Рассмотрим две возможных реализации вычисления (150) при
будет очень значительным. Какой способ выбрать? С точки зрения точных вычислений все они эквивалентны. Но в условиях влияния ошибок округления появляются значительные различия. Рассмотрим две возможных реализации вычисления (150) при  :
: ,
,
 ,
,
 раз. Различия есть и в информационных связях между отдельными операциями. Хотя оба графа имеют одно и тоже число вершин и соответствуют одному и тому же вычисляемому выражению (150), эти графы не изоморфны (у них разные длины критических путей), перенос информации в соответствующих им схемах осуществляется принципиально различными способами. Как видно из первого графа, схема последовательного суммирования не имеет никаких параллельных ветвей вычислений. второй граф показывает наличие в схеме сдваивания большого числа информационно не связанных между собой, а значит имеющих возможность выполняться одновременно, операций.
раз. Различия есть и в информационных связях между отдельными операциями. Хотя оба графа имеют одно и тоже число вершин и соответствуют одному и тому же вычисляемому выражению (150), эти графы не изоморфны (у них разные длины критических путей), перенос информации в соответствующих им схемах осуществляется принципиально различными способами. Как видно из первого графа, схема последовательного суммирования не имеет никаких параллельных ветвей вычислений. второй граф показывает наличие в схеме сдваивания большого числа информационно не связанных между собой, а значит имеющих возможность выполняться одновременно, операций. на подмножества
на подмножества  , где
, где  содержит только входные вершины, а в вершины из множества
содержит только входные вершины, а в вершины из множества  входят дуги лишь из вершин, принадлежащих множествам
входят дуги лишь из вершин, принадлежащих множествам  . Независимо от порядка выполнения операций, каждая из вершин
. Независимо от порядка выполнения операций, каждая из вершин  даст один и тот же результат. Действительно, аргументами операций являются входные данные, эти данные не зависят от порядка выполнения операций. Результаты выполнения операций в
даст один и тот же результат. Действительно, аргументами операций являются входные данные, эти данные не зависят от порядка выполнения операций. Результаты выполнения операций в  , тогда результаты выполнения операций в
, тогда результаты выполнения операций в 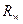 , определяемым временем задержек
, определяемым временем задержек 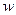 , поскольку частным выбором векторов
, поскольку частным выбором векторов  определяет совокупность обобщенных временных разверток. Задание вектора реализации
определяет совокупность обобщенных временных разверток. Задание вектора реализации  также эквивалентно заданию некоторого вектора
также эквивалентно заданию некоторого вектора 


