
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности численного результата задачиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Алгоритмы, в соответствии с которыми решение поставленных задач сводится к арифметическим действиям, называются численными алгоритмами. Численные алгоритмы занимают очень существенное место среди всевозможных алгоритмов, включающих, например, логические - алгоритмы, в соответствии с которыми решение поставленных задач сводится к логическим действиям,например, алгоритм поиска пути на графе. При решении произвольной реальной задачи в общем случае невозможно получить точное значение искомого численного результата [53,55,60]. Существование неустранимой погрешности в математической модели объекта или процесса, фигурирующего в задаче (математическое описание задачи является неточным), погрешности входных данных, многие из которых в реальных условиях получены экспериментально, погрешность численного алгоритма, используемого для решения, и вычислительная, погрешности, возникающие при каких-либо дополнительных воздействиях на объект, которые часто трактуются как возмущения входных данных, приводят к необходимости их совокупного учета при оценке погрешности результата. Даже в случае, когда входные данные математической модели не имеют погрешностей, а алгоритм, выбранный для решения полученной математической задачи является точным [54], избежать вычислительной погрешности при проведении вычислений в системе чисел с плавающей точкой, а значит и погрешности в полученном результате, невозможно [69]. После построения математической модели реального процесса, которая необходимо удовлетворяет требованию адекватности (решение математической задачи, полученное с ее помощью, незначительно отличается от истинного решения реальной задачи), исходная задача и ее математическая формализация в процессе решения и анализа полученного результата, как правило, не разделяются. Однако, в силу особенностей машинной арифметики, невозможно в общем случае получить точное решение даже смоделированной математической задачи (пренебрегая неустранимой погрешностью и погрешностью метода) [53,60]. Действительно, для конечной системы чисел с плавающей точкой Множество чисел с плавающей точкой
где Часть Таким образом, очевидно, что точно в системе Пусть Идеальным для выполнения арифметических операций в системе Рассмотрим гипотетическую систему
при этом результат правой части:
Очевидно, результат даже такого простого выражения зависит от порядка выполнения операций. Таким образом, одному алгоритму, записанному «на бумаге», соответствует множество «машинных» алгоритмов, в каждом из которых свой порядок выполнения действий, а значит, может быть и другой результат. Полученное приближенное (в силу перечисленных выше причин) решение некоторой вычислительной задачи
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 893; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

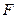 , реализованной в ЭВМ для представления бесконечного множества вещественных чисел
, реализованной в ЭВМ для представления бесконечного множества вещественных чисел  , арифметические операции обладают своими особенностями: основные законы арифметики могут нарушаться. Рассмотрим это подробнее.
, арифметические операции обладают своими особенностями: основные законы арифметики могут нарушаться. Рассмотрим это подробнее. , основанием системы счисления
, основанием системы счисления 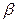 , границами
, границами 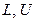 изменения показателя степени
изменения показателя степени  , при том, что каждое число
, при том, что каждое число  представляется в виде:
представляется в виде: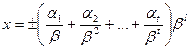 , (200)
, (200) - целые числа, такие, что
- целые числа, такие, что  , а
, а 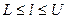 .
.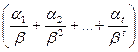 в (200) – дробная часть, или мантисса числа
в (200) – дробная часть, или мантисса числа 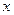 . Система
. Система 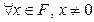 выполняется:
выполняется: 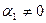 .
. . Результат выполнения арифметических операций над
. Результат выполнения арифметических операций над 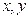 в системе
в системе 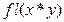 , где символ «*» может быть конкретизирован операцией сложения, вычитания, умножения, деления.
, где символ «*» может быть конкретизирован операцией сложения, вычитания, умножения, деления.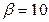 ,
,  , и вычислим в этой системе сумму 0.12+0.17+0.87. В точной арифметике 0.12+(0.17+0.87)=(0.12+0.17)+0.87. В системе
, и вычислим в этой системе сумму 0.12+0.17+0.87. В точной арифметике 0.12+(0.17+0.87)=(0.12+0.17)+0.87. В системе 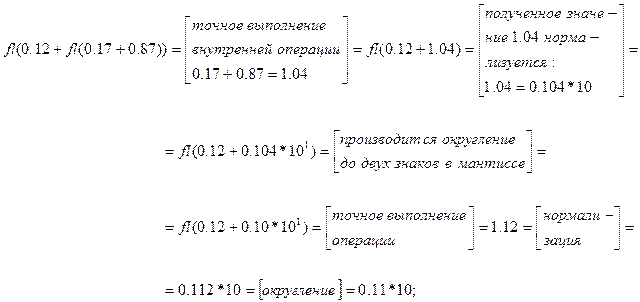
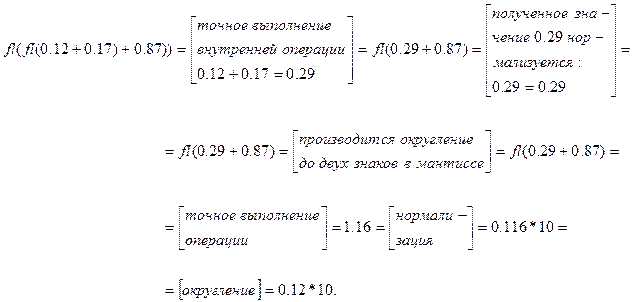
 может рассматриваться как точное решение, но другой, возмущенной задачи
может рассматриваться как точное решение, но другой, возмущенной задачи  (
(


