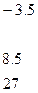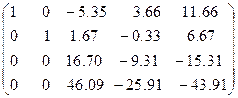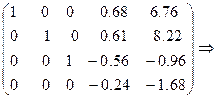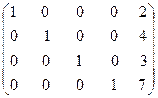Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление значений многочленаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
К задаче вычисления значения многочлена приводят многие задачи, Например, вычисление значений тригонометрических функций, которое осуществляется путем предварительного разложения функции в степенной ряд с последующим подсчетом усеченной суммы этого ряда (которая представляет из себя многочлен). Общий вид многочлена:
Будем предполагать, что все коэффициенты известны и записаны в массив
Для
Конец цикла Возврат
Вычислительная сложность – 3n.
Схема Горнера.
Для
Конец цикла Возврат
Вычислительная сложность – 2n. Предварительная обработка коэффициентов. Результат можно еще улучшить, если обработать коэффициенты до начала вычислений. Основная идея: выразить многочлен через многочлены меньшей степени. Например, для вычисления
Для того, чтобы метод предварительной обработки коэффициентов работал, нужно, чтобы многочлен был унимодальным (т.е. Многочлен представляется в виде: Рассмотрим пример:
Многочлены
На следующем шаге мы можем применить ту же самую процедуру к каждому из многочленов
В результате:
Для вычисления
Способ Умножения Сложения Стандартный 13 7 Схема Горнера 7 7 Предварительная обработка 5 10
Способ Умножения Сложения Стандартный 2N-1 N Схема Горнера N N Предварительная обработка
В последнем алгоритме удалось сэкономить
Решение системы линейных алгебраических уравнений Система Один из способов решения СЛАУ – метод последовательной подстановки:
Такая процедура хорошо работает, но здесь производится очень много алгебраических преобразований, в которые легко может вкрастся ошибка. При возрастании числа уравнений и неизвестных время на выполнение этих преобразований быстро растет. Метод Жордана-Гаусса. СЛАУ можно представить матрицей с
Со строками матрицы можно выполнить некоторые преобразовавния, которые приведут к следующему результату:
Пример.
Делим первую строку на ее первый элемент, затем подбираем для нее коэффициенты таким образом, чтобы при умножении на коэффициент и сложении с ккакой-либо из оставшихся строк элементы первого столбца обнулялись
Повторим эти действия для второй строки.
Для итерационных методов решения операций меньше, но нужно выполнить условия сходимости итерационного процесса. Рассмотрим метод простой итерации Вопросы
Литература
4. Воеводин В.В. Вычислительные основы линейной алгебры / В.В.Воеводин. — М.: Наука. Гл.ред.физ.-мат.лит., 1977. — 304 с. Семестровий модуль 2. АНАЛИЗ ПОСЛЕДОВАТЕЛЬНЫХ АЛГОРИТМОВ ДЛЯ ИСПОЛЬЗОВАНИЯ В ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМАХ Лекция 8.Граф информационной зависимости реализации алгоритма – основной способ представления алгоритма для выявления внутреннего параллелизма План
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1476; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.54.188 (0.011 с.) |

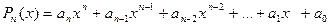
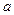 . Значение нужно вычислить в т.
. Значение нужно вычислить в т. 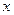 .
.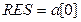 ,
, 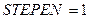
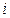 от 1 до
от 1 до 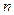
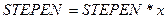
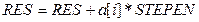
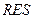
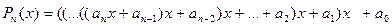 .
.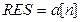
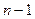 до 0
до 0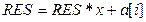
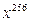 можно в цикле выполнить 255 умножений, а можно
можно в цикле выполнить 255 умножений, а можно 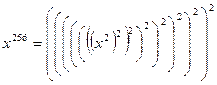 . Положим
. Положим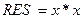
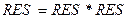 - 7 раз
- 7 раз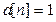 ), а степень многочлена на 1 меньше некоторой степени двойки (
), а степень многочлена на 1 меньше некоторой степени двойки (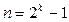 для некоторого
для некоторого 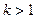 ). Преимущества описываемого подхода могут оказаться настолько велики, что иногда стоит добавить к многочлену слагаемые, позволяющие его применить, а затем вычесть добавленные значения из окончательного результата. Например, если мы имеем дело с многочленом 30 степени, то нужно прибавить к нему
). Преимущества описываемого подхода могут оказаться настолько велики, что иногда стоит добавить к многочлену слагаемые, позволяющие его применить, а затем вычесть добавленные значения из окончательного результата. Например, если мы имеем дело с многочленом 30 степени, то нужно прибавить к нему 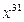 , найти разложение, а затем вычесть
, найти разложение, а затем вычесть 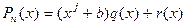 , где
, где 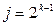 . В обоих многочленах
. В обоих многочленах 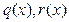 будет вдвое меньше членов, чем в
будет вдвое меньше членов, чем в 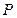 . Для получения нужного результата мы вычислим по отдельности
. Для получения нужного результата мы вычислим по отдельности 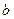 , то оба многочлена
, то оба многочлена 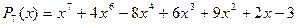 . Определим
. Определим 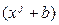 . Поскольку степень многочлена равна 7, то
. Поскольку степень многочлена равна 7, то 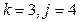 . Выберем значение
. Выберем значение 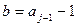 . Для нашего примера
. Для нашего примера 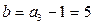 . Теперь мы хотим найти
. Теперь мы хотим найти 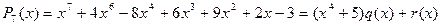 .
.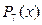 на
на 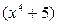 . Деление с остатком дает:
. Деление с остатком дает: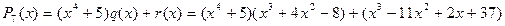
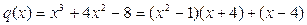 ;
; 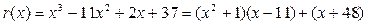
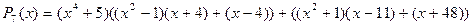 .
.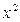 - одно умножение. Еще одно умножение для
- одно умножение. Еще одно умножение для 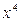 .
.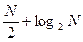
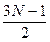
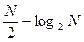 умножений за счет дополнительных
умножений за счет дополнительных 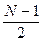 сложений по сравнению со схемой Горнера. Во всех существующих вычислительных системах обмен умножений на сложения считается выгодным, поэтому предварительная обработка коэффициентов повышает эффективность.
сложений по сравнению со схемой Горнера. Во всех существующих вычислительных системах обмен умножений на сложения считается выгодным, поэтому предварительная обработка коэффициентов повышает эффективность.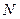 уравнений с
уравнений с 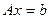 .
.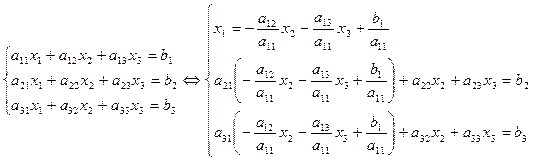
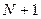 столбцами:
столбцами: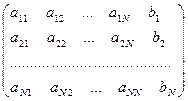
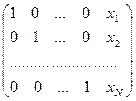 .
.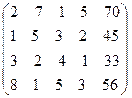 .
.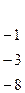
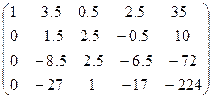 .
.