
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполяционный многочлен ЛагранжаСодержание книги Поиск на нашем сайте
Для каждого узла интерполяции
Систему многочленов Нетрудно построить полиномы 1) многочлен 2) многочлен
равен 1 при Итак, для любого
Введем многочлен
Заметим, что производная многочлена
Теперь многочлен
По построению многочлен Следовательно, многочлен
является интерполяционным многочленом для таблицы (1.1) (имеет степень не выше Формулу (1.7) называют интерполяционной формулой Лагранжа, а полином Замечание 1.4. Число арифметических операций необходимых для вычисления по формуле (1.7) имеет порядок Пример. Найдем интерполяционный многочлен Лагранжа для В этом случае формула (1.7) примет вид:
Графиком функции Задание. Найдите интерполяционные многочлены Лагранжа для Замечание 1.5. Поскольку интерполяционный многочлен (1.7) линейно зависит от значений функции
Погрешность интерполяции Погрешностью интерполяции называется разность
Очевидно, что в узлах интерполяции
В остальных точках погрешность интерполяции, вообще говоря, отлична от нуля. Замечание 1.6. Из предложения 1.1 следует, что погрешность интерполяции Найдем погрешность интерполяции для многочлена степени В этом случае Следовательно,
где Продифференцировав по
так как Отсюда найдем
Однако, для произвольной функции, заданной только таблицей (1.1), ничего конкретного сказать о погрешности интерполяции нельзя. Если функция Теорема 1.2. Если
где Доказательство. Будем разыскивать погрешность интерполяции в виде (1.9), положив
Зафиксируем произвольное
Очевидно, что Таким образом, Учитывая, что для любого
получаем
Следовательно,
и
Теорема доказана. Важное замечание 1.2. Из формулы (1.11) следует, что погрешность интерполяции зависит от выбора узлов интерполяции Замечание 1.7. Из доказательства теоремы 1.1 получаем, что
Следствие 1.2. Пусть
Важный пример (погрешность линейной полиномиальной интерполяции). Пусть
Наибольшее значение Отсюда по формуле (1.13) получаем максимальную оценку погрешности линейной интерполяции
Если Найдем оценку погрешности интерполяции при минимальных требованиях к гладкости функции Пусть
Действительно, используя формулу (1.15), имеем
Поскольку
Так как
Оценка (1.17) доказана. Если имеется таблица большого числа значений некоторой функции
Замечание 1.8. Для класса
|
||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.79.165 (0.007 с.) |

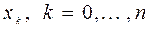 найдем многочлен
найдем многочлен  степени
степени  , равный нулю во всех узлах, кроме
, равный нулю во всех узлах, кроме  - ого, в котором он равен 1:
- ого, в котором он равен 1: .
. принято называть базисом Лагранжа.
принято называть базисом Лагранжа.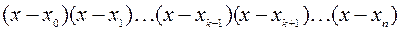 равен нулю во всех узлах интерполяции, кроме
равен нулю во всех узлах интерполяции, кроме 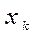 ;
;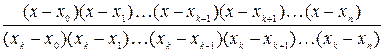
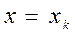 и равен нулю во всех остальных узлах.
и равен нулю во всех остальных узлах.

 .
. (
( )-ой степени, построенный по узлам интерполяции:
)-ой степени, построенный по узлам интерполяции: .
. равна
равна .
. . (1.6)
. (1.6) имеет степень
имеет степень  и равен нулю во всех остальных узлах интерполяции.
и равен нулю во всех остальных узлах интерполяции. (1.7)
(1.7) ,
,  ).
).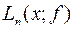 - интерполяционным многочленом Лагранжа.
- интерполяционным многочленом Лагранжа. .
.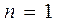 .
. .
. является прямая, проходящая через точки
является прямая, проходящая через точки  и
и  . Такая полиномиальная интерполяция называется линейной полиномиальной (не путать с линейным интерполированием (см. важное замечание 1.1)).
. Такая полиномиальная интерполяция называется линейной полиномиальной (не путать с линейным интерполированием (см. важное замечание 1.1)). .
. , то интерполяционный многочлен для суммы функций равен сумме интерполяционных многочленов слагаемых.
, то интерполяционный многочлен для суммы функций равен сумме интерполяционных многочленов слагаемых.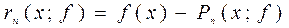 . (1.8)
. (1.8)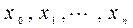
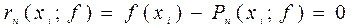 .
. для любой функции
для любой функции  , где
, где  - пространство многочленов степени не выше
- пространство многочленов степени не выше 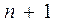 (
( ,
,  ).
). есть многочлен степени
есть многочлен степени 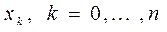 являются его корнями.
являются его корнями. , (1.9)
, (1.9)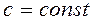 .
.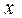 это равенство
это равенство  ,
,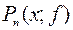 - многочлен степени
- многочлен степени 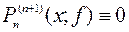 .
. . Таким образом, для
. Таким образом, для  погрешность интерполяции имеет вид
погрешность интерполяции имеет вид . (1.10)
. (1.10) (
( - пространство функций
- пространство функций  ), то для погрешности интерполяции можно получить формулу, аналогичную (1.9).
), то для погрешности интерполяции можно получить формулу, аналогичную (1.9). , то для любого
, то для любого  погрешность интерполяции определяется формулой
погрешность интерполяции определяется формулой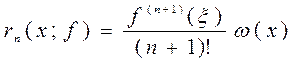 , (1.11)
, (1.11) - некоторая точка отрезка
- некоторая точка отрезка  ).
). ,
, .
.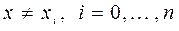 и рассмотрим вспомогательную функцию
и рассмотрим вспомогательную функцию  от переменной
от переменной  :
:
 и обращается в нуль в
и обращается в нуль в  точках отрезка
точках отрезка 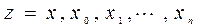 . По теореме Ролля функция
. По теореме Ролля функция  (производная от функции
(производная от функции  ) обращается в нуль, по крайней мере, в
) обращается в нуль, по крайней мере, в  точках отрезка
точках отрезка  , функция
, функция  равна нулю по крайней мере в
равна нулю по крайней мере в  точках этого отрезка,
точках этого отрезка, 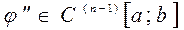 и так далее.
и так далее.
 обращается в нуль, по крайней мере, в одной точке
обращается в нуль, по крайней мере, в одной точке 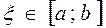 и
и  .
.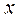
 и
и 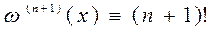 ,
, .
.
 , где
, где  .
. .
.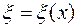 удовлетворяет условию
удовлетворяет условию .
. и
и 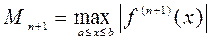 . Тогда
. Тогда , для любого
, для любого  , (1.12)
, (1.12) , (1.13)
, (1.13) (1.14)
(1.14) . Обозначим
. Обозначим  ,
, 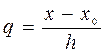 ,
,  . В этом случае
. В этом случае  и интерполяционный многочлен может быть записан в виде
и интерполяционный многочлен может быть записан в виде (1.15)
(1.15) на отрезке
на отрезке  достигается в точке
достигается в точке  и
и 
 . (1.16)
. (1.16) то, оценка (1.16) не имеет места.
то, оценка (1.16) не имеет места. удовлетворяет условию Липшица на отрезке
удовлетворяет условию Липшица на отрезке  , то есть для любых
, то есть для любых  выполнено неравенство
выполнено неравенство  где
где  . Тогда максимальная оценка погрешности линейной интерполяции имеет вид
. Тогда максимальная оценка погрешности линейной интерполяции имеет вид . (1.17)
. (1.17)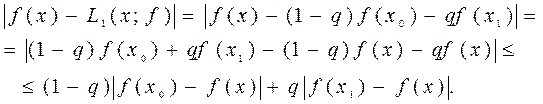
 и
и 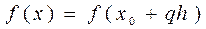 имеем
имеем ,
, .
.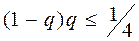 при
при  , то
, то .
. с постоянным шагом
с постоянным шагом  изменения аргумента, то для вычисления значения
изменения аргумента, то для вычисления значения  в заданной точке
в заданной точке  обычно поступают следующим образом. Выбирают два соседних узла, между которыми находится
обычно поступают следующим образом. Выбирают два соседних узла, между которыми находится  , а правый – за
, а правый – за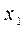 и
и  вычисляют по формуле линейной интерполяции (1.15). Погрешность интерполяции для
вычисляют по формуле линейной интерполяции (1.15). Погрешность интерполяции для  оценивается по формуле (1.16).
оценивается по формуле (1.16). в (1.12)-(1.14) улучшить (уменьшить) нельзя, так как для случая
в (1.12)-(1.14) улучшить (уменьшить) нельзя, так как для случая 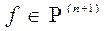 неравенство (1.12) превращается в равенство. Что касается величины
неравенство (1.12) превращается в равенство. Что касается величины  , то она существенно зависит от выбора узлов интерполяции и, следовательно, может быть уменьшена при специальном выборе узлов.
, то она существенно зависит от выбора узлов интерполяции и, следовательно, может быть уменьшена при специальном выборе узлов.


