
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кусочно-полиномиальная интерполяцияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Локально-интерполяционные формулы Разделим отрезок
Выберем на каждом
где Совокупность этих многочленов порождает на отрезке
Таким образом, функция На каждом частичном отрезке
Наиболее часто в практике используется локальная интерполянта для равноотстоящих узлов. Разделим отрезок
Выберем на каждом
Здесь расстояние между любыми соседними узлами интерполяции равно На каждом частичном отрезке
Построим на всем отрезке
Локальная интерполянта
Замечание 3.1. Если общая степень параметром, за счет которого можно повышать точность приближения, является При Если
Отсюда получаем оценку погрешности для локальной интерполянты с равноотстоящими узлами (3.3)-(3.4):
Предложение 3.1. Для
со скоростью Утверждение предложения 3.1. следует из оценки (3.6). Теперь можно указать способ построения сходящегося интерполяционного процесса для любой непрерывной функции с помощью локальной интерполянты. Теорема 3.1. Для любой функции
Доказательство. Введем оператор
По построению Теперь утверждение теоремы 3.1 означает, что последовательность операторов Выполнение условия б) теоремы 2.1 немедленно следует из предложения 3.1, так как множество Докажем справедливость условия б). Обозначим через Имеем
Обозначив
перепишем (3.7) в виде
Сделаем в (3.8) замену переменной, положив
Имеем
Подставляя найденные выражения в (3.7), получим функцию
Так как функция
Отметим, что в (3.10) вычисляется максимальное значение функции
зависит только от Используя (3.12), имеем
Отсюда для нормы оператора
Условие a) теоремы 2.1 доказано. Так как
Интерполяция сплайнами Понятие сплайна. Построенный нами в предыдущем пункте локальный интерполянт Термин сплайн (англ.- spline) имеет техническое происхождение. Первоначально сплайнами называли длинные гибкие деревянные рейки, используемые английскими кораблестроителями для вычерчивания деталей корпуса корабля в натуральную величину. Другими словами, сплайн был чертежным инструментом для построения гладких кривых. В вычислительной математике под сплайном на отрезке Пусть отрезок
Набор точек Сплайном степени
степени не выше Из определения следует, что для многочленов (3.14), представляющих сплайн на каждом частичном отрезке
Таким образом, сплайн – это функция, склеенная из многочленов
Для сплайнов степени
где число Сплайн называется интерполяционным для заданной таблицы (1.1), если
где Интерполяция посредством сплайнов называется сплайн-интерполяцией. Замечание 3.2. Непрерывная кусочно-линейная функция (ломаная) является сплайном первой степени нулевого порядка (дефект равен 1). На практике чаще всего используются сплайны третьей степени второго порядка. Такие сплайны называют кубическими. Выбор значения гладкости
|
|||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 838; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.210.35 (0.01 с.) |

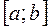 на
на  частичных отрезков точками
частичных отрезков точками .
. - том отрезке
- том отрезке 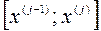 ,
, 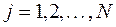 узлы интерполяции
узлы интерполяции  и построим для функции
и построим для функции  интерполяционный многочлен степени не выше
интерполяционный многочлен степени не выше  :
: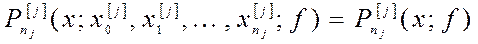 ,
, - номер частичного отрезка,
- номер частичного отрезка, 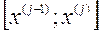 .
. , которую мы назовем локальным интерполянтом функции
, которую мы назовем локальным интерполянтом функции  . (3.1)
. (3.1) определена на всем отрезке
определена на всем отрезке  (склеена из многочленов, интерполирующих функцию
(склеена из многочленов, интерполирующих функцию  не обязательно гладкая (даже непрерывная) в точках склейки
не обязательно гладкая (даже непрерывная) в точках склейки  интерполяционных многочленов. Этот способ приближения функции
интерполяционных многочленов. Этот способ приближения функции  на отрезке
на отрезке  погрешность локальной интерполяции для гладкой функции
погрешность локальной интерполяции для гладкой функции  (3.2)
(3.2) ,
,  .
. на
на  (3.3)
(3.3) ,
, 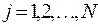 узлы интерполяции
узлы интерполяции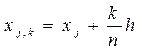 ,
,  . (3.4)
. (3.4)
 построим для функции
построим для функции  :
: . (3.5)
. (3.5) ,
,  , интерполирующих функцию
, интерполирующих функцию 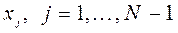 :
: .
.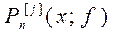 не зависит от номера
не зависит от номера  локальный интерполянт есть кусочно-линейная функция (ломаная) с вершинами в точках
локальный интерполянт есть кусочно-линейная функция (ломаная) с вершинами в точках  , при
, при  графиками многочленов
графиками многочленов  на частичных отрезках
на частичных отрезках  , то погрешность локальной интерполяции для
, то погрешность локальной интерполяции для  (
( ) оценивается по формуле:
) оценивается по формуле:
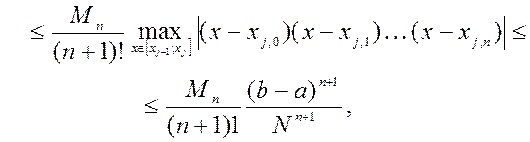
 .
.  (3.6)
(3.6) .
.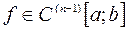 интерполяционный процесс, порожденный локальной интерполянтой
интерполяционный процесс, порожденный локальной интерполянтой  к
к  на
на 
 при
при  интерполяционный процесс, порожденный локальной интерполянтой
интерполяционный процесс, порожденный локальной интерполянтой  для равноотстоящих узлов, определяемых формулами (3.3)-(3.4), равномерно сходится при
для равноотстоящих узлов, определяемых формулами (3.3)-(3.4), равномерно сходится при  ,
,  .
. - линейный ограниченный оператор в пространстве
- линейный ограниченный оператор в пространстве  .
.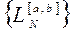 поточечно сходится при
поточечно сходится при  к единичному оператору
к единичному оператору  ,
,  и нам нужно только проверить выполнение условий а) и б) теоремы 2.1 для последовательности
и нам нужно только проверить выполнение условий а) и б) теоремы 2.1 для последовательности  плотно в
плотно в  - оператор интерполирования на отрезке
- оператор интерполирования на отрезке  (см. (3.4)).
(см. (3.4)).
 (3.7)
(3.7) , (3.8)
, (3.8) (3.9)
(3.9)
 ,
, .
. от новой переменной
от новой переменной  :
: . (3.10)
. (3.10) взаимно однозначно отображает отрезок
взаимно однозначно отображает отрезок  , то
, то (3.11)
(3.11) , непрерывной на отрезке
, непрерывной на отрезке  , независящей от
, независящей от  и
и  - номера отрезка
- номера отрезка  (3.12)
(3.12) .
.

 . (3.13)
. (3.13) не зависит от
не зависит от  . Эта задача решается с помощью сплайнов.
. Эта задача решается с помощью сплайнов. понимают кусочно-полиномиальную функцию гладкую на всем отрезке.
понимают кусочно-полиномиальную функцию гладкую на всем отрезке.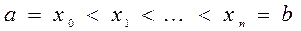 .
. принято называть сеткой.
принято называть сеткой. порядка
порядка  на отрезке
на отрезке  , совпадающая на каждом частичном отрезке
, совпадающая на каждом частичном отрезке  с многочленом
с многочленом (3.14)
(3.14) (3.15)
(3.15)










 Рис. 3.1
Рис. 3.1
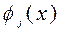 так, что в результате получается
так, что в результате получается  ,
,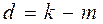 называется дефектом сплайна.
называется дефектом сплайна. , (3.16)
, (3.16) объясняется, в том числе, и тем, что при движении режущего инструмента в автоматизированных металлообрабатывающих комплексах по траектории, являющееся дважды непрерывно дифференцируемой кривой не возникают ударные нагрузки. В случае разрывов второй производной по второму закону Ньютона они появляются и могут привести к разрушению инструмента или дефектам обрабатываемой поверхности. При этом значение степени
объясняется, в том числе, и тем, что при движении режущего инструмента в автоматизированных металлообрабатывающих комплексах по траектории, являющееся дважды непрерывно дифференцируемой кривой не возникают ударные нагрузки. В случае разрывов второй производной по второму закону Ньютона они появляются и могут привести к разрушению инструмента или дефектам обрабатываемой поверхности. При этом значение степени  является минимальным для обеспечения существования интерполяционного сплайна класса
является минимальным для обеспечения существования интерполяционного сплайна класса  для любой таблицы (1.1).
для любой таблицы (1.1).


