
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполяционный полином Лагранжа.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть дана таблица значений
Требуется составить полином (функцию) y = f (x) степени m ≤ n – 1, который принимал бы заданные значения yi при соответствующих значениях xi: yi = f (xi) (i = 1, 2, 3, ………n). Иными словами график функции должен проходить через заданные точки M (xi; yi) Данная задача выполнима при использовании интерполяционного полинома Лагранжа:
....+ или
где
Пример 2.1 Составить полином Лагранжа, удовлетворяющий таблице1 значений Таблица 1
Решение. Вспомогательная функция Вычислим -сначала найдем производную
-затем вычислим Тогда по формуле (1)
= х + 1 Таким образом, в данном случае в качестве интерполяционного полинома найдена линейная функция f (x) = х + 1. Интерполяционная формула Ньютона. Пусть у0, у1, у2,....... – значения некоторой функции y = f (x), соответствующие равноотстоящим значениям аргументам х0, х1, х2,....... (т.е. хk+1 – xk = Δ x =h- const- шаг). Введем обозначения: Δ у0 = у1 – у0, Δ у1 = у2 – у1, Δ у2 = у3 – у2,........., Δ уп-1 = уп – уп-1 - разности первого порядка данной функции; Δ2 у0 = Δ у1 – Δ у0, Δ2 у1 = Δ у2 – Δ у1,............. – разности второго порядка ....................................................................................................................................................... Δ п+1у0 = Δ пу1 – Δ пу0, Δ п+1у1 = Δ пу2 – Δ пу1,............. – разности (п+ 1)- го порядка Производя последовательные подстановки, получим: Δ2 у0 = у2 -2у1 + у0, Δ3 у0 = у3 -3у2 +3 у1 – у0 ,........ Подобным же образом получаем: у1 = у0 + Δ у0, у2 = у0 + 2 Δ у0 + Δ2 у0, у3 = у0 + 3 Δ у0 + 3 Δ2 у0 + Δ3 у0,......
Запишем таблицу разностей: х0 у0 Δ у0 х1 у1 Δ2 у0 Δ у1 Δ3 у0 х2 у2 Δ2 у1 Δ4 у0 Δ у2 Δ3 у1 х3 у3 Δ2 у2 Δ у3 х4 у4 .................................................... Если в формуле (3) положить, что п – не только целое и положительное число, а может быть любым п = t, то получим интерполяционную формулу Ньютона
Мы получили такую функцию от t, которая обращается при t = 0 в у0, при t = 1 в у1 , при t = 2 в у2 и т. д. Поскольку последующее значение аргумента х при постоянном шаге h определяется формулой xn = x0 + nh, то
Пример 2.2: Из таблицы 2: Найти значение у при х = 3,1, пользуясь интерполяционной формулой Ньютона, а также саму интерполяционную функцию (из табл.2 следует, что шаг по х равен h=1). Решение. Составим таблицу разностей:
Здесь х0 = 3, х = 3,1, h = 1. (выбирается из таблицы 2 ближайшее число к 3.1, и шаг то же). Тогда Интерполяционная формула Ньютона (4) для этого случая: Следовательно Интерполяционная функция Ньютона (3*) Упражнения.
(Ответ: у =
(Ответ: у =
(Ответ: у =
(Ответ: у =2х - 1)
lg 2,0 = 0,30103, lg 2,1 = 0,32222, lg 2,2 = 0,34242, lg 2,3 = 0,36173, lg 2,4 = 0,38021, lg 2,5 = 0,39794. Пользуясь интерполяционной формулой Ньютона, найти lg 2,03. (Ответ: lg 2,03 = 0,30750)
(Ответ: у = 4х2 - 7х+ 9)
(Ответ: у =8 + 4(х - 3) + (х – 3)(х - 2)+
(Ответ: у = х3 + х2 + х + 1) ГЛАВА III.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.209.215 (0.009 с.) |

 +
+ +......
+...... (1)
(1) (2)
(2) - вспомогательная функция п -й степени, в которой xi – заданные табличные значения аргумента, а
- вспомогательная функция п -й степени, в которой xi – заданные табличные значения аргумента, а  .
.
 последовательно при данных значениях хi:
последовательно при данных значениях хi: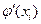 :
:  ,
,  ,
,  ,
, 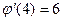 .
. =
=
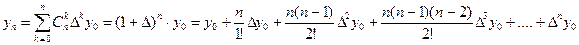 (3)
(3) (4)
(4) . Тогда, полагая x = x0 + th,
. Тогда, полагая x = x0 + th,  приведем формулу (3) к виду
приведем формулу (3) к виду (3*)
(3*)

 , т.е. при х = 3,1 у = 13,71
, т.е. при х = 3,1 у = 13,71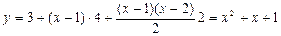
 (х4 - 26х3 + 220х2 – 664х + 640))
(х4 - 26х3 + 220х2 – 664х + 640)) (- 2х3 -15х2 + 25х -9))
(- 2х3 -15х2 + 25х -9))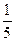 (х3 -13х2 + 69х -92))
(х3 -13х2 + 69х -92)) (х – 3)(х - 2)(х – 1) +
(х – 3)(х - 2)(х – 1) +  (х – 3)(х - 2)(х – 1)х, f(-0,5)= 0,700, f(2,5)= 5,658.)
(х – 3)(х - 2)(х – 1)х, f(-0,5)= 0,700, f(2,5)= 5,658.)


