
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполяционный полином в форме Ньютона.Содержание книги Поиск на нашем сайте
Интерполяционный полином Ньютона имеет вид:
где
Пример 4.6. Построить интерполяционный полином в форме Ньютона, проходящий через точки, заданные таблицей 4.10. Решение. Расчеты представим в виде таблицы.
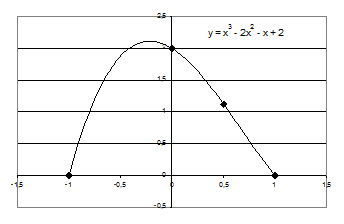
Пример 4.7. Построить интерполяционный полином, проходящий через точки, заданные таблицей 4.10, используя программу Excel. Порядок решения. 14) Ввести таблицу в рабочий лист Excel (обыкновенные дроби вводятся как формулы, т.е. =9/8). Выделить ячейки таблицы. 15) Вызвать Мастер диаграмм. Выбрать тип диаграммы – точечная (без соединительных линий). Нажать кнопку «Готово». 16) Вызвать контекстное меню (правой кнопкой мыши) одной из точек графика. Выбрать пункт «добавить линию тренда». 17) На вкладке тип выбрать полиномиальная аппроксимация и установить степень полинома на единицу меньше числа точек, т.е. 3. 18) На вкладке параметры отметить «показывать уравнение на диаграмме». 19) Закрыть окно настроек, нажав кнопку ОК. Появляется линия графика интерполирующей функции и соответствующая формула:
Численное интегрирование. Требуется вычислить определенный интеграл:
Выберем на отрезке интегрирования
и интерполируем функцию
которая называется квадратурной формулой интерполяционного типа. Метод прямоугольников. На каждом отрезке Поэтому приближенно I вычисляется по формуле (см. рис. 5.1):
Для равноотстоящих узлов формула (5.3) имеет следующий вид:
Или
Формулу (5.4) называют формулой левых прямоугольников, а (5.5) - правых прямоугольников. Программа вычисления интеграла методом прямоугольников представлена на рис. 5.2.
Метод трапеций. В этом методе на каждом отрезке По формуле Лагранжа:
Интегрируя
Суммируя по всем
Для равноотстоящих узлов
или
Программа вычисления интеграла методом трапеций: в программе, представленной на рис. 5.2, заменить отмеченные строки на следующие: 1 S=S+0.5*(FNF(x)+FNF(X+H))*H X=X+H 5.3. Метод парабол (Симпсона). Интервал По формуле Лагранжа:
Интегрируя
Суммируяформулу (5.14)по всем
или
Программа вычисления интеграла методом парабол (Симпсона): в программе, представленной на рис. 5.2, заменить отмеченные строки на следующие: 1 S=S+(FNF(X)+4*FNF(X+H)+FNF(X+2*H))*H/3 X=X+2*H
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 465; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.142.146 (0.007 с.) |



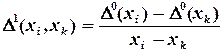 - разделенная разность первого порядка,
- разделенная разность первого порядка, - разделенная разность второго порядка,
- разделенная разность второго порядка,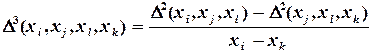 - разделенная разность третьего порядка и т.д.
- разделенная разность третьего порядка и т.д.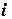
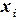
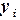


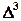


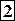


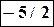
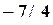
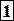
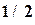
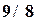
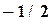
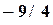
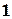
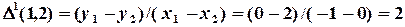
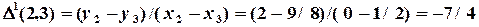
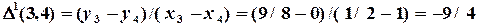
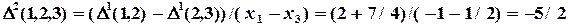
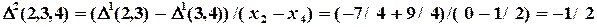
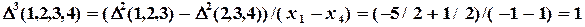
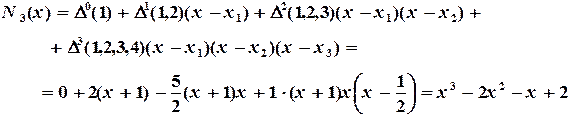

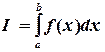 (5.1)
(5.1)
 различных узлов
различных узлов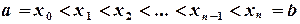
 по ее значениям в этих узлах некоторым полиномом
по ее значениям в этих узлах некоторым полиномом  . Тогда определенный интеграл (5.1) приближенно можно вычислять по формуле
. Тогда определенный интеграл (5.1) приближенно можно вычислять по формуле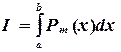 , (5.2)
, (5.2)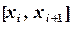 ,
, 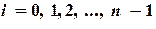 функция
функция 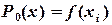 .
.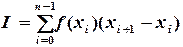 (5.3)
(5.3)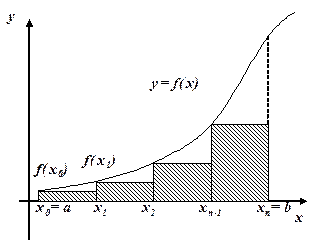
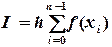 ,
,  (5.4)
(5.4)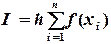 (5.5)
(5.5)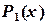 .
. (5.9)
(5.9) (5.10)
(5.10)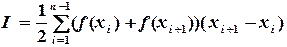 (5.11)
(5.11)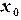 ,
, 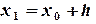 , …,
, …, 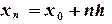 формула (5.11) принимает следующий вид:
формула (5.11) принимает следующий вид: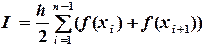 (5.12)
(5.12) (5.13)
(5.13)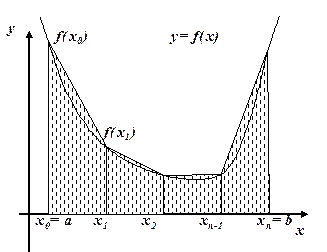
 отрезков. Группируя узлы тройками
отрезков. Группируя узлы тройками 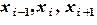 , на каждом отрезке
, на каждом отрезке 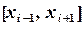
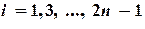 интерполируемфункцию
интерполируемфункцию 

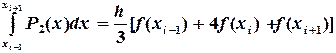 (5.14)
(5.14) (5.15)
(5.15) (5.15)
(5.15)



