
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка точности решения дифференциального уравнения.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Для практической оценки погрешности решения дифференциального уравнения проводят вычисления с шагами
где
Для достижения заданной точности вычисления повторяют, последовательно уменьшая шаг. Процесс вычислений заканчивается, когда для очередного значения
Разностные методы решения краевой задачи для обыкновенного дифференциального уравнения. Линейная краевая задача имеет вид:
при Решение задачи (6.12)-(6.13) проводится в следующей последовательности: 1. Определение сетки: Отрезок [a,b] делится на
2. Определение сеточной функции
3. Аппроксимация уравнения: Для каждой узловой точки
Получаем ситему 4. Решение СЛАУ. Система Пример 6.4. Решить краевую задачу методом конечных разностей с шагом
Решение. Решение проводим в следующей последовательности: 1. Определение сетки:
2. Определение сеточной функции
3. Аппроксимация уравнения:
Получим систему четырех линейных алгебраическихуравнений с четырьмя неизвестными
или
4. Решение системы методом прогонки. Значения
Прямой ход прогонки. Определяем прогоночные коэффициенты
Обратный ход прогонки. Вычисляем Поскольку
Сеточную функцию
Задачи линейного программирования. Общая постановка задачи линейного программирования (ЛП) включает целевую функцию
ограничения типа равенств
и ограничения типа неравенств
В задачах ЛП в число ограничений очень часто входит условие положительности переменных:
Обычно оно связано с тем, что
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 1012; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |

 и
и 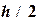 . За оценку погрешности решения, полученного с шагом
. За оценку погрешности решения, полученного с шагом 
 - значение сеточной функции в
- значение сеточной функции в 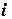 -й точке, вычисленное с шагом
-й точке, вычисленное с шагом 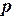 - порядок точности, равный
- порядок точности, равный 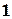 для метода Эйлера, 2 для модифицированного метода Эйлера и 4 для методаРунге-Кутта 4-го порядка.
для метода Эйлера, 2 для модифицированного метода Эйлера и 4 для методаРунге-Кутта 4-го порядка. , где ε ‑ заданная точность.
, где ε ‑ заданная точность.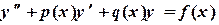 (6.12)
(6.12) (6.13)
(6.13)

 .
. частей:
частей: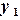

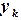

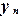







 ,
,  ,
, 
 :
: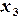
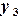
 заменяем функции и производные в уравнениях 6.12-6.13 конечноразностными аналогами:
заменяем функции и производные в уравнениях 6.12-6.13 конечноразностными аналогами:

 т.е.
т.е. 


 (6.14)
(6.14)
 т.е.
т.е. 
 линейных алгебраических уравнений для определения
линейных алгебраических уравнений для определения  :
:


 | | | |
| | | |



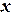
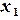 ,
,  - краевые точки,
- краевые точки,  - внутренние точки.
- внутренние точки.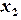
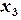



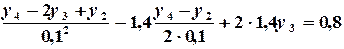


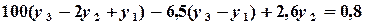



 ,
,  ,
,  ,
,  записываем в виде таблицы 6.1.
записываем в виде таблицы 6.1.
 и
и  (
(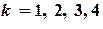 ).
).





 , т.к.
, т.к. 

 ).
). , то
, то  .
.


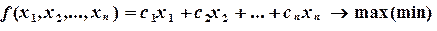 (7.1)
(7.1)
 (7.2)
(7.2)
 (7.3)
(7.3) ,
,  (7.4)
(7.4)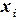 в этих задачах означает количество объектов
в этих задачах означает количество объектов 


