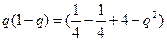Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первая интерполяционная формула НьютонаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть для функции Необходимо подобрать полином
Условия (1) эквивалентны тому, что
Следуя Ньютону, будем искать полином в виде
Т.о. задача сводится к определению коэффициентов Полагая Далее находим первую конечную разность Откуда: Беря затем вторые разности и т.д., получаем:
Введем в рассмотрение новую переменную
(
Это и есть первая интерполяционная формула Ньютона, которая применяется для интерполирования функций Если в (5) положить n=1, то получим формулу линейного интерполирования
При n=2 – формулу параболического или квадратичного интерполирования.
Если дана неограниченная таблица Если таблица конечна, то n не может превышать k-1, где k – число строк таблицы. При применении 1-ой интерполяционной формулы Ньютона удобно пользоваться горизонтальной таблицей разностей. Пример: Построить на отрезке [3,5;3,7] интерполяционный полином Ньютона для функции
Решение:составляем таблицу разностей
Т.к.
где Можно упорядочить полином по степеням х, подставив значение q.
2. Вторая интерполяционная формула Ньютона. Для интерполирования функции в конце таблицы применяется вторая интерполяционная формула Ньютона.
Вывод формулы аналогичен выводу 1-ой интерполяционной формулы, только теперь коэффициент полинома
Введем обозначение Тогда
и так далее. В результате получим:
Пример: дана таблица значений
Найти lg1044
Решение: составляем таблицу конечных разностей
Примем По формуле (3) получем:
Т.о. первая интерполяционная формула Ньютона применяется для интерполирования вперед и экстраполирования назад (за границы интервала); Вторая формула – для интерполирования назад и экстраполирования вперед. Операция экстраполирования менее точна. Оценки погрешностей интерполяционных формул Ньютона Если узлы интерполирования
Где (Для интерполирования При расчетах порядок n разностей выбирается таким, что можно положить:
При этом остаточные члены интерполяционных формул Ньютона будут равны
Пример: В пятизначных таблицах логарифмов даются логарифмы целых чисел от х=1000 до х=10000 с предельной абсолютной погрешностью, равной Решение: Т.к. Отсюда
Из формулы (1) при n=11 и h=1 получаем:
Т.к.
Окончательно получаем:
Т.о. погрешность интерполирования не превосходит погрешностей исходных данных! Линейное интерполирование (h=1) возможно. Интерполяционные формулы Ньютона используют лишь значения функций, лежащие лишь по одну сторону от выбранного начального значения Для интерполирования в середине таблицы удобно применять формулы, содержащие как последующие, так и предшествующие значения функций по отношению к начальному ее значению. При этом используются центральные разности Интерполяционные формулы, построенные с помощью центральных разностей - это формулы Гаусса, Стирлинга, Бесселя.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1033; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.144.162 (0.009 с.) |

 заданы значения
заданы значения  для равноотстоящих узлов
для равноотстоящих узлов 
 , где
, где  - шаг интерполяции.
- шаг интерполяции.
 (3)
(3) , при
, при  .
. (4)
(4)
 , получим
, получим  .
. и полагая
и полагая 



 - число шагов, необходимых для достижения точки
- число шагов, необходимых для достижения точки  из точки
из точки 
 ), получим
), получим (5)
(5) (6)
(6)
 , то n выбирают так, чтобы
, то n выбирают так, чтобы  .
. , заданной таблицей, с шагом h=0,05.
, заданной таблицей, с шагом h=0,05.


 то n=3.
то n=3.
 или
или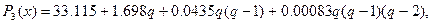


 (коэффициент
(коэффициент  ) определяется из равенств
) определяется из равенств (8)
(8)


 (9)
(9) семизначных логарифмов:
семизначных логарифмов:


 Тогда
Тогда  .
. В результате все знаки верные.
В результате все знаки верные.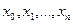 - равноотстоящие причем
- равноотстоящие причем 
 то, пологая
то, пологая  , получим остаточные члены для 1-ой и 2-ой интерполяционных формул Ньютона:
, получим остаточные члены для 1-ой и 2-ой интерполяционных формул Ньютона: (10)
(10) , (11)
, (11) - некоторое промежуточное значение между узлом интерполирования
- некоторое промежуточное значение между узлом интерполирования  , для экстраполирования возможно, что
, для экстраполирования возможно, что  ).
). . Учитывая, что h достаточно мало и
. Учитывая, что h достаточно мало и 
 (12)
(12)
 . Возможно ли линейное программирование с той же степенью точности?
. Возможно ли линейное программирование с той же степенью точности?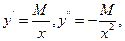 где
где 

 , а
, а 

 (интерполируем не далее, чем на 1 шаг), то
(интерполируем не далее, чем на 1 шаг), то