Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение систем линейных алгебраических уравнений методом итерацийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим систему линейных алгебраических уравнений
Если все диагональные элементы
где
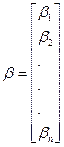
Введем обозначения
Тогда система (2) запишется в виде
В качестве начального приближения
.........
Если существует предел x последовательности векторов
Достаточное условие сходимости итерационного процесса: Теорема. Если какая-нибудь норма матрицы А меньше единицы: Под нормой матрицы
Пример: для матрицы
В расчетах полагают
где
Введем обозначения
Тогда система (2) запишется в виде
В качестве начального приближения
.........
Если существует предел x последовательности векторов
Достаточное условие сходимости итерационного процесса: Теорема. Если какая-нибудь норма матрицы А меньше единицы:
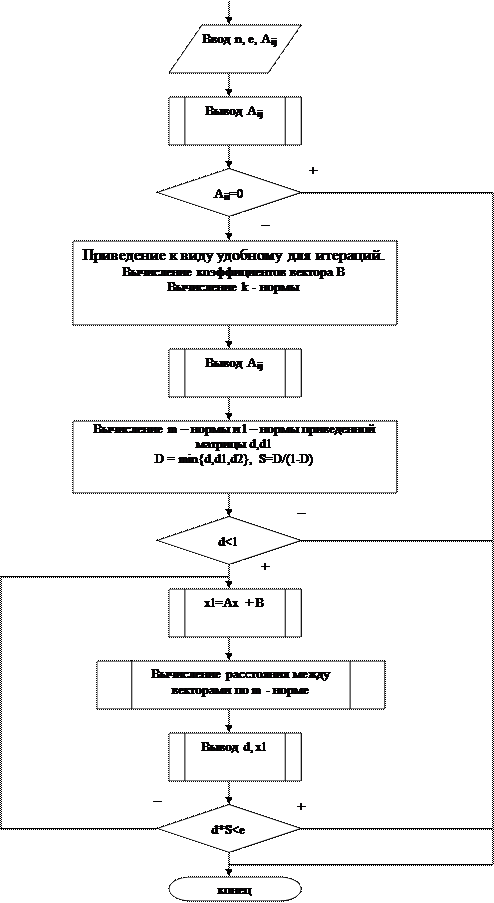
Рис. 2.1 Блок-схема решения системы линейных алгебраических уравнений Под нормой матрицы
Пример: для матрицы
В расчетах полагают
где
Из неравенства (13) можно получить оценку числа итераций k, необходимых для обеспечения заданной точности e. Отклонение приближения
Для вывода (14) достаточно рассмотреть равенства:
Далее И учитывая, что В неравенствах (13) и (14) используются согласованные нормы для матриц и векторов, т.е. m и l-нормы. Неравенство (14) дает завышенную оценку числа итераций k. Из (14) можно получить удобное условие, позволяющее принять приближение
Пример: Найти решение системы уравнений
методом итераций с точностью 10-2. Решение: Приведем систему к виду (10)
Запишем последовательность итераций
Для приведенной матрицы
В качестве начального приближения возьмем вектор-столбец свободных членов приведенной системы Число итераций для достижения заданной точности
Вычислим теперь три последовательных приближения по формулам (15) и оценим погрешность каждого результата, используя неравенство (13) в виде:
Первое приближение:
Следовательно,
Далее последовательно находим:
Третья итерация:
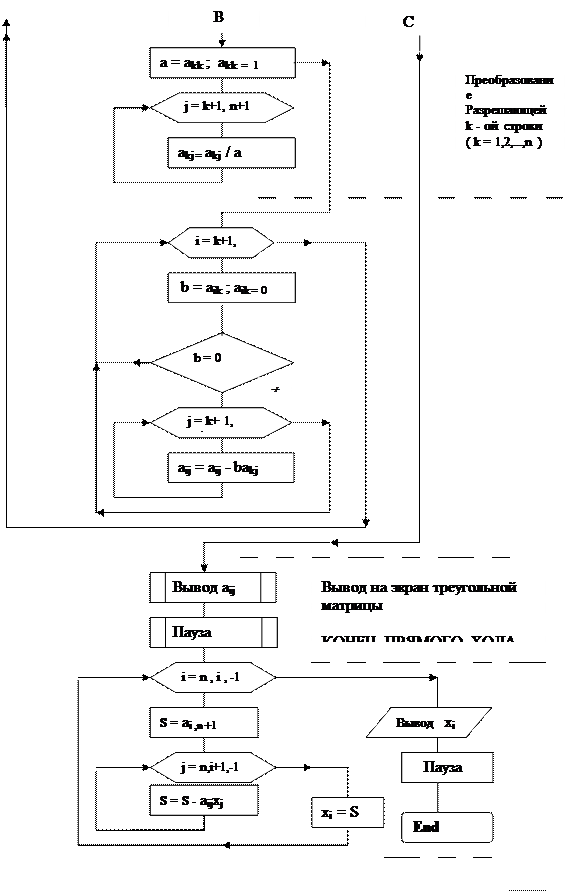
Заданная точность достигается за 5 шагов. Точное решение Ниже приведена блок – схема алгоритма решения системы линейных алгебраических уравнений методом итераций.
Лабораторная работа 2
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.120.119 (0.006 с.) |

 (9)
(9)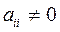
 , то систему (1) можно представить в приведенном виде
, то систему (1) можно представить в приведенном виде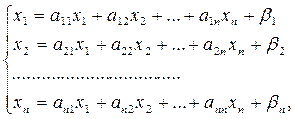 (10)
(10)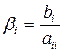
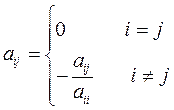
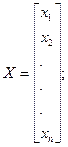
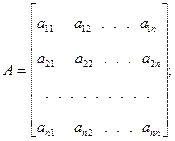
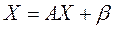 (11)
(11) возьмем вектор b и подставим его в уравнение (11). Получим
возьмем вектор b и подставим его в уравнение (11). Получим  .Продолжая процесс, получим последовательности приближений:
.Продолжая процесс, получим последовательности приближений: - первое приближение
- первое приближение -второе приближение (12)
-второе приближение (12)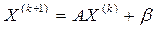 - (k+1)-ое приближение.
- (k+1)-ое приближение.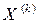 то, переходя к пределу в равенстве
то, переходя к пределу в равенстве 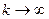 , убеждаемся, что x является решением уравнения (11), т.е.
, убеждаемся, что x является решением уравнения (11), т.е.
 , то уравнение (11) имеет единственное решение x, к которому стремится последовательность итераций (12) при любом выборе начального приближения.
, то уравнение (11) имеет единственное решение x, к которому стремится последовательность итераций (12) при любом выборе начального приближения.
 понимают следующие выражения:
понимают следующие выражения: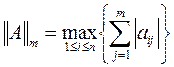 (m-норма) сумма модулей элементов строки
(m-норма) сумма модулей элементов строки (l-норма) сумма модулей элементов столбца
(l-норма) сумма модулей элементов столбца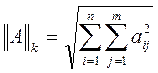 (k-норма)
(k-норма)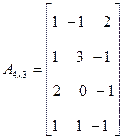

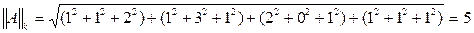
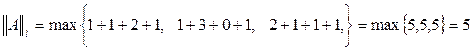
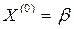 . Погрешности приближенного решения уравнения (11) на k-ом шаге оценивают неравенством
. Погрешности приближенного решения уравнения (11) на k-ом шаге оценивают неравенством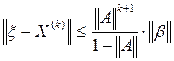 , (13)
, (13)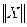 - норма вектора X
- норма вектора X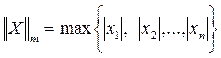 m-норма или кубическая норма
m-норма или кубическая норма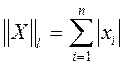 l-норма или октаэдрическая норма
l-норма или октаэдрическая норма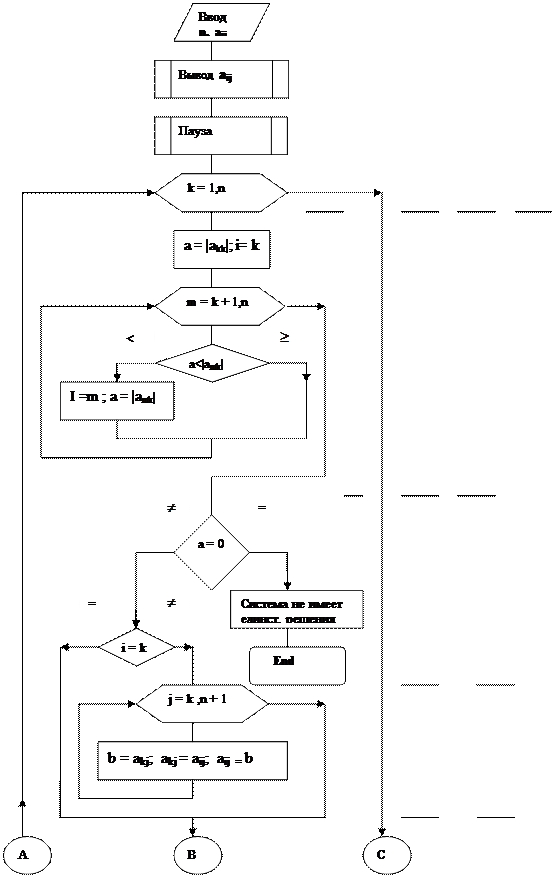
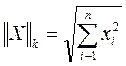 k-норма или сферическая норма.
k-норма или сферическая норма. (14)
(14)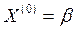 ;
;  ;
; 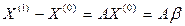 ;
;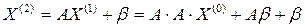 ;
;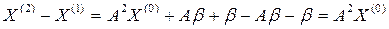 ; и т.д.
; и т.д.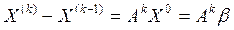
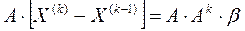 .
.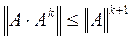 , т.к. норма
, т.к. норма  .
. (15)
(15)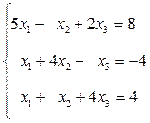
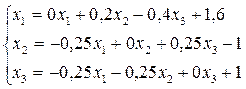
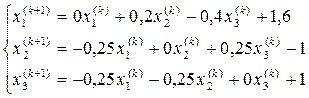 (16)
(16)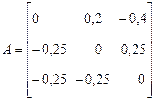 достаточное условие ходимости выполняется по m-норме:
достаточное условие ходимости выполняется по m-норме: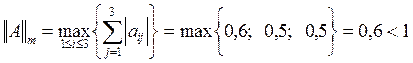
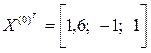 .
.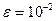 определяем из неравенства (13)
определяем из неравенства (13)  , которое запишем так:
, которое запишем так: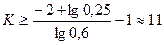 , действительно:
, действительно: 
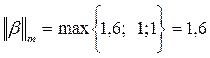 .
.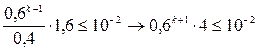 ;
; 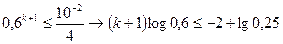 т.к.
т.к. 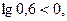 то
то  ;
;  .
.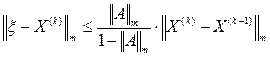 .
. 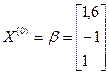
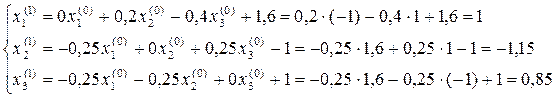
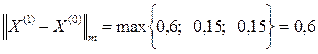
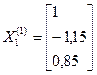 дает значение корня ξ с погрешностью, не превышающей величины
дает значение корня ξ с погрешностью, не превышающей величины  .
.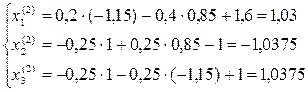
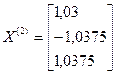 ;
; 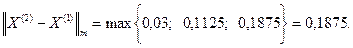

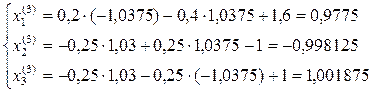
 ;
; 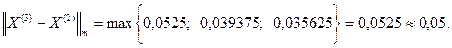
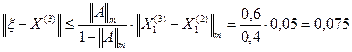
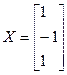 .
.