
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы решения типовых задач кдп и ПВСодержание книги
Поиск на нашем сайте
В инженерной практике с целью решения уравнений описываемых уравнениями с обыкновенными производными преимущественно применяют численные методы. Существуют различные методы решений этих уравнений. Наиболее распространёнными являются. 5.2.2.1. Методы, использующие разложение в ряд Тейлора [8, 9, 10]
При численном решении дифференциальных уравнений фундаментальное значение имеет разложение в ряд Тейлора в окрестности точки. Если решение дифференциального уравнения типа уравнения (2.11) известно, что yo - решение уравнения в точке хо, то значение зависимой переменной y1 в близлежащей точке х1 может быть выражено в виде
где h = x1 – x0, a при х = х0. Хотя (2.12) представляет собой бесконечный ряд, этот ряд, как правило, сходится достаточно быстро, поэтому для выражения yi с заданной точностью достаточно конечного числа членов. Это означает, что члены в правой части уравнения (2.12) последовательно уменьшаются, становясь в конце концов пренебрежительно малыми. По существу разложение в ряд Тейлора представляет собой метод решения обыкновенных дифференциальных уравнений. Для любых заданных хо, yo и h остается лишь найти необходимое число высших производных y и подставить эти величины в (2.12). Этот процесс может быть затем последовательно повторен для нахождения y2, y3 и т.д. 5.2.2.2. Метод Эйлера [10, 11] Метод Эйлера основан на том, что не учитываются все члены в ряде Тейлора, содержащие вторую и более высокие степени h. Иначе говоря, мы полагаем
Очевидно, что предсказанное значение для y1 будет иметь ошибку e, определяемую выражением
Подобная ошибка будет вводится на каждом шаге вычисления. Заметим, однако, что, в то время как в уравнении (2.13) единственной является ошибка, выражаемая формулой (2.14), это уже не будет справедливым при вычислении y2 или y3 и т. д. В уравнении (2.13) член yо известен точно, тогда как соответствующие члены при последующем вычислении становятся все более неточными. Поэтому ошибки от отбрасывания членов стремятся накапливаться в процессе вычисления, и в конце концов они превзойдут предел допустимой ошибки. Тем не менее метод Эйлера в силу его простоты широко используется на практике в тех случаях, когда рост ошибки может тщательно контролироваться.
5.2.2.3. Методы Рунге-Кутта [10,11, 13, 14] Со временем были разработаны разнообразные численные методы, которые призваны были, сохранив полезное свойство «самоначинания» описанного выше метода Тейлора, устранить в то же время основной недостаток – необходимость вычисления высших производных. Наиболее важные и широко используемые из этих методов известны как методы Рунге-Кутта, хотя кроме Рунге-Кутта значительный вклад в их разработку внесли такие исследователи, как Хейн, Нистром и многие другие. По существу основной подход, содержащийся в этих методах, состоит в решении уравнения вида y /= f (x, y), y = yо при х = хо (2.15) путем вычисления dy/dx не только при yо, но также в трех или большем числе близко примыкающих точек в областях х и y. Решение для первого шага вычисления, т.е. y1, получается путем вычисления суммы полученных таким образом выражений для dy/dx с разными весовыми коэффициентами. Очевидно, главный недостаток метода состоит в том, что функциональная зависимость, выражаемая правой частью уравнения (2.15), должна быть определена для четырех или более значений х и y на каждом шаге вычисления. В случае сложного характера функции f (x, y) эти вычисления могут потребовать львиной доли машинного времени и составляют главный камень преткновения. Тем не менее, как уже указывалось, среди различных «самоначинающихся» методов методы Рунге-Кутта образуют самый мощный и широко используемый подход. Методы Рунге-Кутта называются методами третьего, четвертого, пятого и т.д. порядков в зависимости от числа членов в уравнении (2.12) ряда Тейлора, при котором достигается его полное соответствие уравнению (2.16).
где ki получаются путём подстановки в уравнение (2.15), а m i – весовые коэффициенты, которые должны быть определены так, чтобы выполнялось условие m 0 + m 1 +…+m р = 1. Таким образом, метод третьего порядка охватывает все члены вплоть до члена, пропорционального h3 включительно, метод четвертого порядка охватывает все члены вплоть до члена, пропорционального h4 включительно, и т.д. Очевидно, что в методе более высокого порядка получается меньшая ошибка на каждом шаге, но вычисление последовательных значений yi сложнее и более трудоемко. На практике редко применяются методы Рунге-Кутта выше пятого порядка.
Не итеративные методы интегрирования вперед [4, 11] Важный класс численных методов для решения дифференциальных уравнений и систем дифференциальных уравнений включает применение формул типа
Если коэффициент bi+1 равен нулю, то все члены в правой части уравнения (2.17) на данном шаге вычисления известны. Решение тогда может быть получено в виде линейной комбинации из решений р предыдущих шагов. Этот метод поэтому нельзя использовать в начале процедуры решения, когда в нашем распоряжении имеются только начальные условия. Вместо этого для первых р шагов необходимо использовать такой метод, как метод Рунге-Кутта, описанный выше. Методы интегрирования вперед обладают преимуществами простоты, легкости программирования и относительно короткого времени вычисления. На каждом шаге вычислений необходимо получить только одно значение y′ = f (x, y). Вместе с тем этот метод в отличие от методов, описанных в последующих разделах, не требует выполнения итерации. Однако точность методов интегрирования вперед относительно низка, а возможность накопления ошибок сравнительно высока. Методы прогноза – коррекции [10, 11] Наивысшая точность может быть получена при использовании методов, аналогичных описанным выше, если коэффициент bi+1 в уравнении (2.17) не полагать равным нулю, т.е. если член, пропорциональный y′i+1, сохраняется при вычислении yi+1. Главная трудность в применении формул интегрирования состоит в том, что член, пропорциональный y′i+1, не известен в тот момент времени, когда должно вычисляться yi+1, Поэтому необходимо применять итеративный метод проб и ошибок. Точнее, необходимо использовать формулу интегрирования вперед для прогнозирования значения yi+1 и потом скорректировать это значение, используя более точную формулу. По указанной причине этот метод называется методом прогноза-коррекции. Существует несколько методов прогноза – коррекции. Различие между ними состоит главным образом в том, в каком сочетании используются формулы прогноза – коррекции.
Методы прогноза – модификации – коррекции [10, 11, 14] Одна из трудностей, возникающих при применении методов прогноза – коррекции при решении сложных задач, состоит в необходимости выполнения последовательных итераций. Частью каждого итеративного шага является вычисление y′ = f (x, y). Когда f (x, y) представляет собой сложное или длинное выражение и когда приходиться решать относительно большие системы уравнений, требуемое для этого метода время вычислений может очень скоро стать чрезмерно большим. На практике было установлено, что одно из основных преимуществ методов интегрирования вперед и методов прогноза – коррекции перед методами Рунге – Кутта состоит в том, что они устраняют необходимость многочисленных вычислений f (x, y) на каждом шаге в области х. Если требуется выполнение многочисленных итераций в методе прогноза – коррекции, это преимущество теряется. Поэтому были разработаны компромиссные методы, значительно улучшающие точность по сравнению с не итеративными методами интегрирования вперед и не требующие выполнения итераций [4].
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.237.68 (0.008 с.) |

 (2.11)
(2.11) (2.12)
(2.12)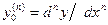
 . (2.13)
. (2.13) . (2.14)
. (2.14) (2.16)
(2.16)



