
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбор схемы решения задачи массопереноса в водеСодержание книги
Поиск на нашем сайте
Большинство методов расчета температуры воды водных объектов, которые описаны в, методических указаниях и различных научных изданиях, предусматривают использование уравнения теплопроводности с некоторыми ограничениями. Например, в работе [7] рекомендуется уравнение
Там же дан краткий обзор существующих методов расчета переноса тепла в водотоке и предложена общая схема решения одномерной задачи с учетом колебания уровня-воды в виде
где Для замыкания решения уравнения (2) необходимо параметризовать профиль температуры и задать краевые условия. В простейшем случае при параметризации
формула (2) преобразуется:
Уравнение (4) описывает тепловой баланс некоторого сечения водотока. Уравнение (2) является квазилинейным из-за нелинейной зависимости его правой части от температуры. В настоящее время метод конечных разностей является единственным, позволяющим найти эффективное решение таких уравнений. При гидрологических расчетах с помощью (2) и (4) выбор конечно-разностной схемы решения имеет важное значение. Это обусловлено малой изученностью гидро- и термодинамики водотоков, отсутствием подробных гидрометеорологических данных наблюдений, а также сложностью реализации балансовых задач на ЭВМ. Ниже на примере уравнений (1) и (4) излагается и анализируется наиболее общий вариант конечно-разностной схемы для решения тепло балансовых задач. Метод конечных разностей физически означает переход от непрерывной среды к некоторой ее дискретной модели, поэтому будем предполагать, что (1) соответствует интегральное уравнение баланса тепла в рассматриваемой области G:
Здесь в, правой части уравнения теплопроводности (1) оставлен диффузионный член по у. Проинтегрируем формулу (5) для элементарного объема со сторонами, параллельными осям координат, делая предположение о линейном характере изменения температуры по всем, координатам. Это допустимо для достаточно малого по размерам объема, в пределах которого процесс теплопередачи равномерный. При численном интегрировании используем следующие допущения и преобразования: t — линейная функция переменных х и τ; q = - λ grad t В реальных условиях теплопоток обусловлен не только градиентом температуры, но и множеством других факторов, подчас вообще не поддающихся учету. Предположение о линейности функции t по каждой из координат при приближенном вычислении соответствующих интегралов дает возможность оставить в формуле трапеций только два члена. Для первого слагаемого уравнения (5) получаем при последовательном численном интегрировании:
Интегрирование второго слагаемого в (5) при сделанных предположениях приводит к выражению
Предполагая линейную зависимость теплопотоков Sпов и Sдна от х и τ и независимость их от у, можно записать правую часть уравнения (5) в виде
Применительно к мелководному и хорошо перемешиваемому водоему значение температуры воды по глубине можно усреднить, тогда (5) после интегрирования представим следующим образом:

Уравнение (6) представляет собой уравнение баланса энергии отсека воды с размерами Δx*b*h (Δx — длина, b - ширина, h — глубина) и является конечно-разностной аппроксимацией дифференциального уравнения (1) с параметризацией (3). Полученная при помощи интегро- интерполяционного метода конечно-разностная аппроксимация должна аппроксимировать и уравнение (4). Проверим это, пользуясь рекомендациями [8]. Уравнение (4) можно рассматривать как уравнение переноса
где: (tк и tн — конечная и начальная температуры), для которого формулируется краевая задача, когда при х=о задано граничное значение tK (0, τ) = μ(τ), τ Построим основную сеть tji (i = 0, 1, 2, 3,...; j=0, 1, 2, 3,...) с постоянными шагами Δx = ti+1 – ti и Δτ = tj+1 - tj. Обозначив эту сеть DΔx,Δτ, введем в рассмотрение сеть DΔx/2,Δτ/2, полученную с помощью DΔx,Δτ добавлением к ней узловых точек {ti+1/2} и { tj-1/2, совпадающих с серединами интервалов [ti, ti+1] и [tj, tj+1] [9]. Используем схему вида
и примем
Полученная схема по форме записи соответствует физике процесса, так как в гидрофизических задачах обычно принимается, что
т. е. правая часть уравнения (8) зависит от средней температуры по Δτ и Δх. Уравнение (6) идентично системе (8)—(10), при этом правая часть найдена не через средние по Ах и Лт интервалы, а в тех же узлах сетки DΔx,Δτ. Правомерность физических и математических допущений, принятых при интегрировании уравнения (5) и выборе схемы (8), можно проверить сведением уравнения (6) к обычному [4, 10] уравнению теплового баланса в теплопотоках с помощью осреднения входящих в (6) величин. Левая часть (6) при этом примет вид: ЛЧ = где: Для правой части уравнения (6) получаем
ПЧ = где:
что соответствует конечно-разностной схеме (8). Выражая скорость через расход соответствующего створа b*h, получаем уравнение теплового баланса призматического отсека воды в виде
где t1, t2 — средняя температура верхнего и нижнего створов; tH, tK—средние значения начальной и конечной температур отсека; Qu Qz — расходы воды через верхний и нижний створы. Рассматривая слагаемые, выражающие адвективный перенос тепла, можно предположить, что Изменение теплосодержания участка водотока за период Δτ можно записать как ΔG=cρbhΔx(tK-tн). Остальные слагаемые характеризуют величину теплопотока через поверхность, дно участка ΣSi, а также боковой теплоприток ΣSб, тогда
G1 – G2 +ƩSσ + ƩSi = ΔG, (12)
что соответствует рекомендациям [10]. Уравнение (12) для расчета термического режима водоема обычно [11] используется в форме (И), которая связывает среднюю, начальную и конечную температуры отсека воды за период Дт с температурой верхнего и нижнего створов участка, а также со средней за тот же период, т. е. соответствует схеме (8). При его применении для практических расчетов вводят связь между температурой воды створов отсека воды и средней температурой отсека
tср = 0,5 (t2 + t1) (13)
а также связь средней по объему температуры воды с конечной и начальной температурами tср = 0,5 (tк + tн). Тогда tк - tн = 2(tср - tк ), t2 - t1 = 2(tср - t1 ) (14)
и уравнение (11) запишется следующим образом: bhΔx(tср – tн) + Δτ(Q2tср – Q1t1) = Уравнение (15) позволяет выполнять расчеты термического режима водоемов, но нечувствительность к изменению уровня по длине водотока и во времени снижает точность результатов. В отличие от (15) в формулах (2) и (4) учитывается распределение температуры, воды по сечению с использованием информации об изменениях морфометрических условий и не стационарности движения воды. Кроме того, эти уравнения идеально приспособлены для реализации на ЭВМ. Рассмотрим частный случай. Пусть
Соответственно схема (8) преобразуется в схему
которая решается методом итераций (подбором численного значения tj-1/2), входящего в правую и левую части уравнения (17)). Интересно отметить, что схема (17) и использованная связь (14) совпадают с рекомендациями Б. А. Браславского [11] для расчета термического режима в непроточном водоеме. Отличие в том, что схема (14) записана в более общем виде и подбор tj-1/2 предусматривается не графоаналитически, а численно на ЭВМ. Для неподвижного водоема Д. И. Бибиковым и Н. Н. Петруничевым [3] приведена графоаналитическая схема решения уравнения (16). В ее основе лежит связь (14), так как решение ищется как среднее за период Δτ. Там же рассмотрен пример решения задачи проектирования распределения температуры по длине водотока. В основу предлагаемого способа положено уравнение (4) при допущениях (13) и при пренебрежении первым членом уравнения (4). Очевидно, что система (8) — (10) является наиболее общим вариантом решения прикладной задачи теплопереноса. Summary The methods of approximation of water channel temperature are compared with the use of the transfer equation. The general formulation of the problem is proposed together with its conventional variants. Литература 1. Методические рекомендации к расчету водохранилищ-охладителей. ТЭС ПЗЗ — 75, ВНИИГ. Я., 1976. 97 с. 2. Указания по термическому расчету водохранилищ/Сост. А. И. Пехович, В. М. Жидких. ВСН 18 — 68, Минэнерго СССР. Л., 1969. 70 с; 3. ВСН 46 — 71, Минэнерго СССР. Л., 1972. 71 с. 4. Бибиков Д. И., Петруничев Н. В. Ледовые затруднения на гидростанциях. М.; Л., 1950. 159 с. 5. Готлиб Я- Л., Жидких В. М.;- Сокольников Н. М. Тепловой режим водохранилищ гидроэлектростанций. Л., 1976. 203 с. 6. Пивоваров А. А. Термика замерзающих водоемов. М., 1972. 140 с. 7. Российский К., И. Термический режим водохранилищ. М., 1975. 167 с. 8. Константинов А. Р., Трушевский В. Л., Химии Н. М. Оценка влияния изъятия стока на тепловой режим проточного водоема (постановка задачи). — В кн.: Гидрометеорологическое обеспечение народного хозяйства. Л., 1982, с. 112—118. 9. Годунов С. К, Рябенький В. С, Разностные схемы. Введение в теорию. М., 1977. 213 c$ 9. М а р ч у к Г. И. Методы вычислительной математики. М.,, 1977. 455 с. 10. Спицын И. П., Винников С. Д., Трушевский В. Л., Дивногорская Е. Ю. Балансовая модель термического режима устьевого взморья (на примере Обской губы). — Труды Арктич. и антарктич. науч.-исслед. ин-та, 1982, т. 378, с. 138—159. 11. Б р а с л а в с к и й А. П., Викулина 3. А. Нормы испарения с поверхности водохранилища. Л., 1964. 212 с. 12. А 1 b i-g n о t I. P., Boutin C, I s a k a H. Estimation du bilan thermique et de la temperature moyenne de la couche de melange d'un lac profond a l'aite de donnes meteorolo-giques de routine. — Archiv fur Meteorologie, Ge'ophysik und Bioklimatologie, Ser. A, 1979, Bd 28, N 1, p. 71—87.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.201.101 (0.01 с.) |

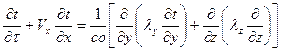 . (1)
. (1)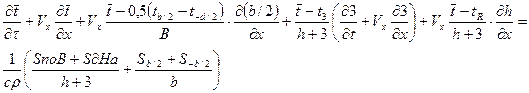 (2)
(2) 
 — средняя по поперечному сечению температура воды; t3=t3(x, τ), th = th(x, τ)—средние температуры поверхности и дна; t+b/2 и t-b/2 — температуры на правом и левом берегах, t+-b/2 = t+-b/2(x, τ); з = з(х, т) — превышения уровня воды над равновесным; h = h(x)—невозмущенная глубина потока; b/2 = b/2(х) — полуширина потока (ось X направлена вдоль осевой линии потока); Sпов, Sдна, Sb/2, S-b/2 — величины удельных теплопотоков через верхнюю, нижнюю и боковые поверхности водотока; V- средняя скорость потока на сечении вдоль оси X; τ — время; с — удельная теплоемкость воды; р — плотность воды.
— средняя по поперечному сечению температура воды; t3=t3(x, τ), th = th(x, τ)—средние температуры поверхности и дна; t+b/2 и t-b/2 — температуры на правом и левом берегах, t+-b/2 = t+-b/2(x, τ); з = з(х, т) — превышения уровня воды над равновесным; h = h(x)—невозмущенная глубина потока; b/2 = b/2(х) — полуширина потока (ось X направлена вдоль осевой линии потока); Sпов, Sдна, Sb/2, S-b/2 — величины удельных теплопотоков через верхнюю, нижнюю и боковые поверхности водотока; V- средняя скорость потока на сечении вдоль оси X; τ — время; с — удельная теплоемкость воды; р — плотность воды. (3)
(3) (4)
(4) . (5)
. (5) =const (т. е. Vx линейно зависит от х) и Vx не зависит от τ;
=const (т. е. Vx линейно зависит от х) и Vx не зависит от τ; 
 .
.

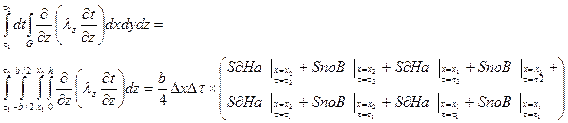
 (7)
(7) 0, и решение ищется при х > 0, τ > 0. При τ = 0 tK (х, 0) = t0(х), x
0, и решение ищется при х > 0, τ > 0. При τ = 0 tK (х, 0) = t0(х), x  (8)
(8) (9)
(9) (10)
(10)
 x,z — результат осреднения температуры по глубине и длине элементарного отсека воды;
x,z — результат осреднения температуры по глубине и длине элементарного отсека воды;  z— результат осреднения скорости движения воды по глубине элементарного отсека; tτ,z — результат осреднения температуры за период времени Δτ = τ2 – τi
z— результат осреднения скорости движения воды по глубине элементарного отсека; tτ,z — результат осреднения температуры за период времени Δτ = τ2 – τi
 Δx, b,Δτ и
Δx, b,Δτ и  ,
, , (11)
, (11) = Q1 = Q2, тогда cρΔτ
= Q1 = Q2, тогда cρΔτ  1,2 представляет собой тепловой приток G1 и сток G2 с рассматриваемого участка с размерами b*h*Δx.
1,2 представляет собой тепловой приток G1 и сток G2 с рассматриваемого участка с размерами b*h*Δx. (15)
(15) или V = 0, тогда из (7) получаем
или V = 0, тогда из (7) получаем (16)
(16) , (17)
, (17)


