
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принципы математического моделирования качества воды водотоковСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для описания процессов формирования качества воды, определяющих трансформацию состава и свойств загрязнённой воды, используют математические модели, которые можно подразделить на две группы: детерминированные и статистические (или вероятностные). Общая схема математического моделирования представлена в соответствии с рисунком 2.1
Рисунок 2.1. Принципиальная схема математического моделирования Особенности протекания процесса конвективно-диффузионного переноса и превращения в общем случае неконсервативных примесей зависят как от самих водных объектов, принимающих сточные воды, так и от состава и характера выпуска последних. Поэтому при построении математических моделей, которые могли бы быть использованы для достоверных инженерных прогнозов, необходима предварительная типизация водных объектов и схематизация процесса в виде расчётной схемы. Это позволит, с одной стороны, учесть основные определяющие процесс факторы, характер водного режима, его гидравлические, морфологические и гидрохимические характеристики; режим и условия выпуска сточных вод; условия самоочищения для различных фаз водного режима и т. д., а с другой, использовать современные типовые методы и средства математического моделирования. Расчеты процессов конвективно-диффузионного переноса (КДП)
Типизация водных объектов по условиям конвективно-диффузионного переноса (КДП) и превращения веществ ПВ должна представлять гидродинамическое, гидрохимическое и гидробиологическое районирование водных бассейнов с выделением однотипных по гидродинамическим, гидрохимическим и гидробиологическим особенностям и возможностям поддержания стабильных биологических процессов и устойчивых экологических циклов расчётных схем участков. Схематизация процесса связана с разработкой различных способов упрощения природной обстановки при решении конкретных задач. Схематизация должна состоять в определённом упрощении природных условий, как в пределах отдельных выделенных участков, так и всего бассейна в целом. На первом этапе производится упрощение природных условий и составление исходной диффузионной и первичной модельной схем, затем выполняется дальнейшая схематизация с применением моделирования, связанная с уточнением расчётных значений элементов модели и вида задания их в окончательной схеме. Третий этап посвящён обоснованию достоверности принятой схематизации и окончательному построению модели. В зависимости от ширины водного объекта выделяются три группы: большие, средние, малые; для рек выделятся четвёртая группа – ручьи. По глубине водные объекты подразделяются на неглубокие – мелкие и средние, и глубокие. Кроме того, для водотоков типы и группы подразделяются в зависимости от скорости течения, шероховатости дна (коэффициент Шези), степени извилистости (коэффициент извилистости).
Построение математической модели качества воды на основе схематизации процесса КДП и ПВ Сущность метода КДП и ПВ В настоящее время при планировании и разработке водоохранных комплексов большое значение имеют расчеты процессов конвективно-диффузионного переноса (КДП) и превращения веществ (ПВ). Именно они обеспечивают стабильность биологических процессов и устойчивость экологических циклов в районах ниже выпуска сточных вод. А характер и интенсивность протекания биологических процессов определяют предельно допустимую нагрузку на водоемы, водотоки, степень очистки сбросных вод и справедливое распределение затрат на очистку между всеми объектами, сбрасывающими сточные воды. При проектировании и строительстве любого водоохранного комплекса необходимо соответствующее теоретическое обоснование. Но точные расчеты гидродинамических процессов конвективно-диффузионного переноса в пространстве и во времени и физико-химические превращения неконсервативных примесей в большинстве случаев невозможны из-за громоздкости или отсутствия аналитического решения уравнения КДП, описывающего распределение концентрации расчетного ингредиента в водоеме или водотоке. Полевые исследования и измерения процессов КДП и ПВ в естественных природных условиях трудны и дороги, кроме того, число возможных вариантов, как правило, во много раз превышает число реально существующих типовых объектов. Поэтому исследователи и проектировщики прибегают к числовым методам расчета или к методам математического моделирования. При производстве исследований широко применяются современные средства вычислительной техники (аналоговые установки, электронные и сеточные вычислительные машины). Они являются не только эффективным средством решения инженерных задач, позволяют экономить много времени, средств и труда, но и открывают новые возможности в области исследований и проектирования. Рассматриваемые вычислительные средства позволяют проводить имитационное моделирование и оптимизацию параметров системы локальных и бассейновых водоохранных комплексов с использованием как детерминированных так и вероятностных моделей или комбинаций. В общем случае процесс формирования качества воды описывается системой гидродинамики и системой турбулентной дисперсии для неконсервативных веществ, которые также могут быть выражены как система конвективно-диффузионного переноса и превращения веществ (КДП и ПВ):

где С – мгновенное значение концентрации; x, y, z – координаты по соответствующим осям; t – временной параметр; Vx, Vy, Vz – средние скорости течения по соответствующим осям; Dx, Dx, Dz – коэффициенты турбулентного переноса или диффузии; с – параметр неконсервативности. Для каждой выбранной группы водных объектов строятся математические модели, состоящие из уравнений движения и турбулентной диффузии. При изотропной турбулентности осреднённая скорость потока постоянна по всей области течения. Поэтому выбирается одна ось координат так, чтобы её направление совпало с направлением основного течения [3, 4,5]. Попытки создания моделей, совмещающих физико-динамические и химико-биологические процессы, обычно приводят к использованию дифференциальных уравнений. К достоинствам последних относится принципиальная возможность установления общих положений теории функционирования экосистем [4]. Типовые модели КДП и ПВ можно классифицировать, в соответствии с рисунком 2. По мерности модели
По типу режима переноса
По граничным условиям
По построению процесса а) в зависимости от направления диффузии
Рисунок 2.2 - схематизация процесса КДП и ПВ В зависимости от типа водного объекта возможно применять одномерные, двухмерные и трёхмерные модели. В случае необходимости получения характера распределения концентраций загрязняющих веществ во времени, а также в случае нестационарной работы источников сброса сточных вод необходимо применять нестационарные модели. На границах задаются граничные условия I-III рода. Возможен учёт турбулентной диффузии как в одном направлении, так и в различных направлениях. Различают также модели, учитывающие неконсервативность примесей и не учитывающие. Однако в случае консервативных примесей возможно использование обоих типов моделей. Основные типы детерминированных моделей приведём в таблице 2.2 [5- 9].
Таблица 2.2 - Основные типы моделей КДП и ПВ
где Q –расход воды, м3/c; k1 – коэффициент биохимического окисления, 1/сут; w - площадь поперечного сечения русла, м2; nx, ny, nz (υx, υy, υz) - средние скорости течения, м/с; Dx, Dy, Dz – коэффициенты продольной, поперечной диффузии и диффузии по вертикали соответственно, м2/c; С – концентрация вещества, мг/л; t – время, с; T – температура воды, 0С; х – продольная координата, м; y – поперечная координата, м; z – координата по вертикали; В – коэффициент; L – длина расчётного участка, м. Эти уравнения используются при прогнозировании качества воды водных объектов с заданными характеристиками сточных вод и при нормировании режимов водоотведения с расчётом норм ПДС сточных вод. На основании проведённого анализа существующих математических моделей и задач нормирования качества воды выделены типы моделей, которые могут быть использованы для практической реализации бассейнового принципа нормирования. Для численной реализации приведенных выше уравнений качества воды водотоков и получения однозначного решения необходимо задание краевых условий. Под краевыми условиями для рассматриваемого типа уравнений будем понимать совокупность граничных, начальных (для нестационарных задач) условий и уравнения баланса вещества. Последнее для установившегося процесса разбавления консервативного вещества имеет вид: Q·Cф + qст ·Сст = (Q + q)·Cср, (2.2) где Q – расход воды в реке до сброса сточных вод, qст – расход сточных вод на сбросе в водный объект; Сст – концентрация расчетного ингредиента в сточных водах непосредственно перед их выпуском в реку; Сф – концентрация расчетного ингредиента в створе выше выпуска сточных вод (фоновом створе); Сср – средняя концентрация расчетного показателя, начиная со створа выпуска сточных вод до створа достаточного перемешивания. Из соотношения (1.3.2) может быть определена величина Сср:
В случае, если фоновая концентрация расчётного ингредиента, Сф = 0 или с учётом превышений концентраций над фоном, то есть для так называемой приведённой концентрации Сприв выражаемой соотношением: Сприв = С - Сф (2.4) где С – действительная концентрация расчётного ингредиента, то уравнение (2.4) может быть представлено в виде:
где
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 805; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.68.228 (0.007 с.) |









 в) в зависимости от типа загрязняющих веществ
в) в зависимости от типа загрязняющих веществ





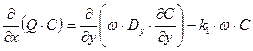









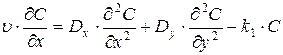


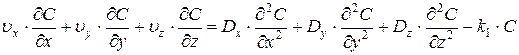 ,
,
 (2.3)
(2.3)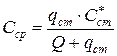 , (2.5)
, (2.5) - приведённая концентрация сточных вод (
- приведённая концентрация сточных вод ( ).
).


