
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практикум «Расчеты тепломассопереноса в реках и водоемах»Содержание книги
Поиск на нашем сайте
Задача 1. Расчёт вертикального распределения температуры воды в водоёме при открытой водной поверхности (без учёта факторов гидродинамики)
Постановка задачи Условиям задачи соответствует уравнение(8) в виде:
И соответствующая конечно-разностная схема (35), которая может быть получена следующим образом. Опустим через водную массу полуось Z от поверхности вниз по направлению к дну водоёма. Тогда решение задачи будет построение графика температуры по глубине для каждого заданного момента времени. Такому решению соответствует, конечно-разностная сетка (рис. 4) с начальными и граничными условиями: при
Рисунок Со стр 17
Для решения уравнения (40) необходимо получить зависимость перехода от одного слоя времени к другому. Получим её для сетки с постоянными шагами как по времени ( Уравнение (40), вписанное в конечных разностях
для точки с координатами
Производная от температуры по времени для узла сетки
Подставляя выражения производных в конечных разностях через углы сетки, получим
откуда
Подбирая величину шагов
получим Таким образом, температура воды в очередном узле сетки ищется как полу сумма температур из выше и нижерасположенных узлов на предыдущем слое времени. Очевидно, что граничное условие поверхности должно быть дополнено граничным условием на заданной глубине (или по дну водоёма). Тогда возможны различные варианты исследования с помощью ЭВМ. Например, при заданных реальных начальным и граничных условиях определяется время достижения температуры поверхности искомой величины. Или при тех же граничных условиях и при условиях гомотермии определяется время выхолаживания (осень) и время прогревания (весна) водоёма. При выводе решения на экран в виде таблицы или графика появляется возможность расширения круга задач по анализу изменения температуры воды по глубине водоёма. Пример решения Рассчитать выхолаживание воды в водоёме за ночь, если в 21 час наблюдалось состояние изотермии, т.е. температура воды по всей глубине равнялась Тепловой поток с поверхности воды
Из условия
Тогда из
Результаты расчёта можно свести в таблицу и представить в виде графиков (рис. 5).
Таблица. Расчет выхолаживания воды в водоеме
Результаты расчёта могут быть представлены в виде графика (рис. 5)
Рис.5. Распределение температуры воды по глубине
Задача 2. Расчёт теплообмена в ложе водоёма Постановка задачи Ограничения: - рассматривается теплообмен, происходящий между грунтом и водой, без учёта тепла геотермического происхождения; - рассматривается плоская (одномерная) задача (что справедливо для неглубоких равнинных водоёмов); - распределение тепла в грунте происходит исключительно за счёт его теплопроводности (без учёта тепломассообмена грунтовыми водами). Рассмотрим количество тепла, передаваемое придонными слоями воды ложу:
и соответствующее тепло, получаемое ложем:
где Тогда, ставя в соответствие изменение температуры во времени изменению теплопотока по нормали к поверхности:
и подставляя в (49) (48), получаем
что соответствует уравнению Фурье
где Будем рассматривать полуплоскость, ограниченную осями a=const при при Z=0, при H=0, где:
При использовании приведённого метода рекомендуется: 1) Интервал времени, обеспечивающий достаточную точность расчёта, принимать равным не более пяти суток. 2) Температуру поверхности дна принимать по температуре придонных слоёв воды. 3) Начальное распределение температуры задавать по линейному закону от температуры поверхности дна до среднемноголетней температуры грунтов. Так как решение является годовой цикл теплообмена в ложе водоёма, представленный серией эпюр температуры, то рекомендуется повторять расчёт годового хода при пяти- и десятилетнем периоде стационирования. При этом в качестве начальных условий при повторном расчёте задавать распределение температур по вертикали, полученное в предыдущем годовом цикле. 4) Окончание расчёта считать достижение пучком эпюр температуры заданного расхождения температур по расчётной глубине. 5) Расчёт вести в предположении, что дно водоёма представляет собой горизонтальную однородную поверхность, а колебания температуры у дна являются периодической функцией. Теплопроводность, плотность и теплоёмкость принимать для песчано-глинистых грунтов.
Пример решения Рассчитать распределение температуры в грунте ложа мелководного водоёма в период открытого русла, если известно, что грунт состоит из влажного песка ( Расчет выполняем в таблице, принимая
Тогда
Представим результаты расчёта в виде таблицы.
Таблица. Расчет теплообмена в ложе водоема
Результаты расчёта могут быть представлены в виде графика (рис. 6)
Рис.6. График хода температуры по глубине
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 643; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |

 (40)
(40)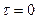
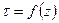 и при
и при 
 .
.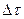 ), так и по глубине (
), так и по глубине ( ).
).
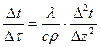 (41)
(41) верно в том случае, если мы учтём различия в изменении температуры по глубине на интервалах выше узла сетки
верно в том случае, если мы учтём различия в изменении температуры по глубине на интервалах выше узла сетки  (42)
(42) (43)
(43)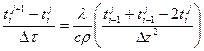
 (44)
(44) , (45)
, (45) . (46)
. (46) .
.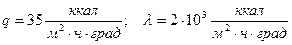 .
.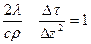 , принимая
, принимая 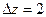 , определяем
, определяем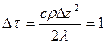
 следует, что постоянная величина
следует, что постоянная величина  для границы атмосфера - вода равна
для границы атмосфера - вода равна


 (47)
(47) (48)
(48)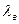 и
и  - соответственно теплопроводность воды и грунта, насыщенного водой;
- соответственно теплопроводность воды и грунта, насыщенного водой;  и
и 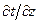 - соответственно градиенты температуры воды в придонном слое и температуры ложа в приводном его слое.
- соответственно градиенты температуры воды в придонном слое и температуры ложа в приводном его слое. (49)
(49) , (50)
, (50) . (51)
. (51)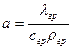 .. (52)
.. (52) ,
,  с условиями однозначности:
с условиями однозначности:


 (53)
(53)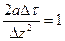 (54)
(54) ) и дано начальное распределение температуры.
) и дано начальное распределение температуры.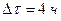 . Из условия (54) следует, что
. Из условия (54) следует, что .
. .
.




