
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая характеристика гидросистемыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
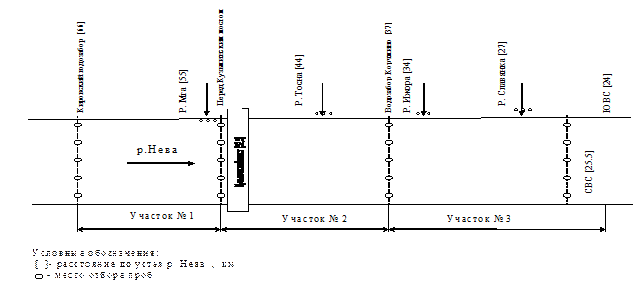
Объектом исследования является нижнее течение р.Невы в пределах Санкт-Петербурга (от впадения р.Славянки до устьевого взморья). В рассматриваемом районе можно выделить 3 участка, существенно отличающихся по гидрологическому режиму: - от р.Славянки до Литейного моста, где Нева течет единым потоком, справа в нее впадает р.Охта, слева отходит Обводный канал; - от Литейного моста до устья Невы, включая дельту Невы, где река делится на 5 основных рукавов - Большая и Малая Нева, Большая, Малая и Средняя Невка, и многочисленные протоки и каналы; - устьевое взморье, или бар Невы, являющийся подводным продолжением дельты. Бар Невы представляет собой систему отмелей, разделенных продольными ложбинами-фарватерами (Елагинский, Петровский, Галерный, Корабельный и Гребной). Длина бара с востока на запад 3-5 км, ширина с севера на юг 12-15 км. Елагинский фарватер собирает в один поток воды Средней и Большой Невок, продолжением Малой Невки является Петровский фарватер, от устья Большой Невы отходят Галерный и Корабельный фарватеры. Искусственным сооружением Невского взморья является Морской канал. На протяжении 12 км он заключен в ограждающие дамбы. Наблюдения за гидрологическими характеристиками р.Невы началось с момента возникновения Санкт-Петербурга. Река Нева в настоящее время одна из наиболее изученных рек страны. Наблюдения за уровнем воды составляют уже примерно 290 лет, период наблюдений за стоком - примерно 140 лет (с 1859 г.). За это время выполнены сотни измерений расходов воды на участке дельты Невы, в каналах и фарватерах взморья. Большинство измерений выполнялось при уровнях воды, близких к ординару, и однотипных гидрометеорологических условиях (в штиль или при слабом ветре)- [4]. Последнее позволяет при выполнении поставленной задачи использовать в качестве расчетных величин среднемноголетние расходы воды различной обеспеченности. В настоящее время регулярные гидрологические и гидрохимические наблюдения в дельте р.Невы выполняются СЗ УГМС. Режим уровней воды в р.Неве существенно отличается от уровненного режима крупных равнинных рек. Эти отличия особенно заметны в нижнем течении реки (дельта), где определяющим фактором колебания уровня является не величина стока воды, а влияние Балтики. Любые колебания водной поверхности моря и, особенно, Финского залива передаются в Невскую губу, значительно усиливаются в ней из-за мелководности, и распространяются вверх по Неве, постепенно затухая. При всем многообразии причин, вызывающих изменения уровня (сгоны, нагоны, приливы и отливы, сейши, длинные волны и др.), для практических целей используется ограниченное число обобщенных характеристик: средний многолетний уровень, максимальный и минимальный годовой уровень редкой повторяемости, продолжительность стояния того или иного уровня. Средний многолетний уровень называется ординаром и по отношению к нему оценивается подъем или спад уровня при нагонах и сгонах. 5.4.1.2. Сток воды р. Невы и его распределение по рукавам дельты (гидравлическая схема расчета) Средний многолетний расход воды у Новосаратовки (ГП 1) составляет 2500 м3/с (за 122-летний период наблюдений) и годовой сток 95% обеспеченности равен 1800 м /с [7]. В работе Нежиховского обобщены материалы наблюдений по 1980 год включительно. Указанный период включает серию лет с очень высокой и очень низкой водностью. Обобщение материалов с учетом последних 2-х десятилетий практически не изменяет величину среднего многолетнего расхода. Вопрос о распределении расхода по рукавам и протокам дельты рассмотрены в работе [28]. В таблице 2 приведены средние многолетние расходы воды в рукавах и каналах дельты при расходе воды на ГП Новосаратовка равном 2500 м3/с и величины расходов в этих водотоках при расходе р.Невы 95% обеспеченности 1800 м3/с. Расходы воды в реках и каналах Санкт-Петербурга (в % от расхода Невы) Распределение между основными рукавами: В Обводный канал и Фонтанку - 2% от расхода в вершине дельты; В Большую Невку - 19%; В Большую Неву - 60%; В Малую Неву-19%. Большая Невка ниже по течению делится на 3 потока: Малая Невка - (8,9%) Средняя Невка - (7,5%) В сумме - 19% Большая Невка-(12,6%) Выйдя из рукавов, водный поток делится по фарватерам взморья следующим образом: Елагинский - 10%, Петровский - 29%, Галерный- 11%, Корабельный - 26%, Гребной - 5%, Пролив между островами Белый и Канонерский - 2%, Морской канал (выше Золотых Ворот) - 17%. Гидравлические параметры, необходимые для расчета качества воды (Qpac4, Vcp, НСр, Вср) для каждого рассматриваемого участка (по техническому заданию) определялись следующим образом: расходы воды (Q) рассчитывались с учетом распределения расхода воды по рукавам и каналам дельты (таблица 2); Vcp, НСр, Вср - определялись как по данным, материалам экспедиционных обследований, выполненных в ГГИ в 1975-85 гг. [арх.ГГИ, №38926, 38943, 38964, 41684, 43341, 43364, 43348, 43959, 24554, 43339, 43342, 43346, 43368, 43365]. При отсутствии измерений на отдельных участках расчетные характеристики определялись путем интерполяции с соседними участками, как путем расчета, так и на основании общих представлений. Для определения плановых размеров (В, L) использовались карты М 1:25000 [10], где приведены также и данные о скоростях течения при различных уровнях воды. Расчетные гидрологические параметры приведены в табл.3, для расхода 2500 м3/с и табл.За - для расхода 1800 м3/с.
Пример расчётной схемы участка реки Нева приведён в соответствии с рисунком 2.7
Рисунок 2.7 – примерная расчётная схема участка реки Невы
Исходя из краткого описания реки Невы, приведённого выше и в главе первой первого тома реку Неву можно отнести: -К глубоким водотокам равнинного типа с большой шириной. - Для расчёта выбираем двухмерную математическую модель, это обусловлено тем, что попытка учесть реальную морфологию в рамках трёхмерной модели до сих пор наталкивается на большие вычислительные трудности, что в первую очередь, связано с отсутствием достаточного ряда данных натурных наблюдений. Общие принципы перехода от трёхмерной задачи к эквивалентным двухмерным путём соответствующих преобразований уравнений по глубине потока развиты в работе Н.А.Картвешвилли [25]. Анализ реального трёхмерного потока показывает, что поток можно рассматривать в рамках двухмерной задачи, если размеры его малы по сравнению с главными радиусами свободной поверхности и дна. При ширине реки значительно превышающей глубину, выравнивание концентраций осуществляется под воздействием горизонтального КДП и ПВ. - Выбираем стационарную модель. Это обусловлено тем, что река Нева характеризуется достаточно стабильными гидрологическими условиями. А изменение характеристик водовыпусков сточных вод не велико. - Задаёмся граничными условиями второго рода, которые характеризуют непроницаемость берегов. - Выбираем изотропную модель, при которой осреднённая скорость потока постоянна по всей области течения. Поэтому выбирается одна ось координат так чтобы её направление совпало с направлением основного течения в нашем случае vx=vср. Коэффициентом продольной диффузии не учитываем, так как скорости в реке Нева около 1 м3/с и конвективная составляющая переноса загрязняющих веществ в направлении основного течения значительно превышает диффузионный перенос - Моделирование проводим для неконсервативных веществ, это связано с тем, что биогенные вещества подвержены процессам самоочищения. Расчетные формулы Из приведённой типизации и схематизации получаем двумерную нестационарную математическую модель формирования качества воды, которая описывается уравнением вида
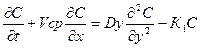
где С- концентрация загрязняющих веществ, Vcp- средняя скорость течения водного объекта, Dy- коэффициент турбулентной диффузии, К1- коэффициент неконсервативности. Для математического решения дифференциального уравнения выбираем метод конечных разностей с граничными условиями второго рода По явной конечно-разностной схеме выбранное дифференциальное уравнение можно представить в виде
Основные принципы: Моделирование ведётся с постоянными характеристиками по сечению каждого участка В направлении течения возможно задание новых гидрологических характеристик: скорости, ширины реки, коэффициентов поперечной диффузии В случае ветвления участка реки, распределение масс загрязняющих веществ происходит пропорционально расходу воды в каждом из водотоков Моделирование ведётся раздельно для каждого из источников загрязнения, общий результат распределения концентраций получается суммированием полей концентраций от всех водовыпусков с полем фоновых значений.
5.4.1.4. Расчётные параметры Для математических расчетов распределения неконсервативных примесей в водотоках распределением концентрации примесей по вертикали потока пренебрегают, также не учитывается фактор времени. В данной системе за основу принято уравнение для однородной изотропной стационарной двумерной модели с учетом самоочищения:
Для расчета этого дифференциального уравнения используется дискретный метод, для чего весь участок реки разбивается на участки, исходя из условий устойчивости. Количество участков по длине и ширине участка реки определяется параметрами Mx и Ny соответственно. При выборе этих параметров должно выполняться соотношение:
где hx – величина шага по длине реки (L / Mx), hy – величина шага по ширине реки (B / Ny), Dy – поперечная диффузия, Vx – скорость течения реки. Расчет поперечной диффузии Поперечная диффузия (Dy) – параметр, определяющий интенсивность распространения загрязнения по ширине участка реки. Он может определяться различными способами, выбор которого должен быть обусловлен гидрологическими характеристиками реки и имеющимися данными. Ниже приведены возможные способы расчёта Dy [3].
Методы расчета поперечной диффузии.
1. Метод Элдера (для лабораторных условий).
2. Метод Потапова (для естественных течений).
3. Метод Караушева (для естественных течений).
4. Метод Банзала (для естественных течений).
5. Комбинированный метод (для естественных течений).
В этих уравнениях: R – гидравлический радиус; J – гидрологический уклон свободной поверхности реки; g – гравитационное ускорение (g = 9,80665); Н – средняя глубина реки; B – средняя ширина реки; Vx – средняя скорость течения реки; Сш – коэффициент Шези; Nш – коэффициент шероховатости русла; f – коэффициент извилистости русла; М, m – вспомогательные коэффициенты. Концентрация начального разбавления (Сн.р.) – начальная концентрация вещества в месте выброса. При расчете начального разбавления для каждого источника любой конфигурации используются следующие соотношения:
где Сср* - среднее значение концентрации (уравнение баланса вещества), Сст – концентрация стока одного источника по одному показателю, Сф – фоновая концентрация, Q – расход воды в реке, q – расход воды в источнике, Ny – число клеток по ширине реки, Nз – число клеток загрязнения. Nз рассчитывается исходя из конфигурации источника, если источник сосредоточенный, то, обычно это одна клетка. Для каждого источника рассчитывается относительное начальное разбавление (за вычетом фоновой концентрации) и все источники помещаются на обнуленное поле концентраций, соблюдая их конфигурацию. Затем происходит перерасчет всего поля концентраций с начала участка и до конца по течению с захватом всех встретившихся источников. Таким образом, концентрация начального разбавления для источника, находящегося ниже по течению относительно другого определяется как его относительная концентрация начального разбавления плюс относительная концентрация вещества в точке выброса плюс фоновая концентрация. Расчет параметров створа В контрольных створах возможен расчёт кратности разбавления,
Кратность разбавления является величиной постоянной для различных значений Сст при фиксированных параметрах модели, что говорит о линейной зависимости максимальной концентрации от концентрации стока. Степень перемешивания, выражаемая в процентах:
характеризует интенсивность разбавления вещества для данной модели. В качестве параметров реки задаются следующие параметры. Длины участка реки (L), ширины участка реки (В), средней глубина реки (Н) и скорость течения (Vx), коэффициента поперечной диффузии Dy. После задания всех параметров выбирают шаг по длине и по ширине реки. Шаги задаются при помощи задания параметров сетки. Шаг по X: hx = L / Mx. (2.41) Шаг по Y: hy = B / Ny. (2.42) Mx – число шагов по длине участка реки, Ny – число шагов по ширине участка реки
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 631; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.146.180 (0.008 с.) |

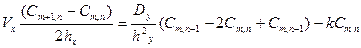 (2.30)
(2.30) (2.31)
(2.31)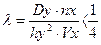 , (2.32)
, (2.32)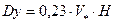 ;
; 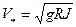 ;
; 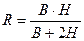 ; (2.33)
; (2.33)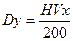 . (2.34)
. (2.34)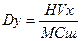 ;
; 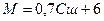 ;
; 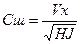 . (2.35)
. (2.35)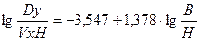 (2.36)
(2.36) ; (2.37)
; (2.37) .
.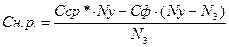 ;
; 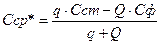 ; (2.38)
; (2.38)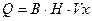 ,
,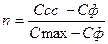
 (2.39)
(2.39)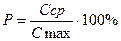 (2.40)
(2.40)


