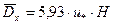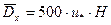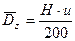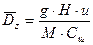Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка параметров для моделей прогнозирования качества воды в исследуемой системеСодержание книги
Поиск на нашем сайте
Все параметры математических моделей формирования качества воды водных объектов могут быть определены по эмпирическим зависимостям [30, 31, 32] или идентифицированы для соответствующих уравнений по натурным данным. Наиболее распространенные эмпирические зависимости для расчета параметров различных математических моделей приведены в работах [1,30,31]. Рассмотрим основные гидравлические элементы потока – геометрические размеры и основные кинематические и динамические величины, характеризующие условия течения. К ним относятся ширина (B), глубина (H), площадь поперечного сечения (w), смоченный периметр (c), гидравлический радиус (R), уклон (I), расход воды (Q), скорость течения (u), шероховатость русла (n) и т.д.. Режим течения в естественных потоках зависит от средней скорости потока uср, гидравлического радиуса R и кинематического коэффициента вязкости воды n. Гидравлическим радиусом потока называется отношение площади поперечного сечения потока w к смоченному периметру c, т.е.
Смоченный периметр – это линия контакта потока со стенками или руслом. Для речных потоков, отличающихся относительно малой глубиной и большой шириной В, гидравлический радиус близок к средней глубине потока. Действительно, в этом случае c = В, а средняя глубина Нср определяется отношением
Средняя скорость при равномерном движении в открытых руслах определяется по формуле Шези
где Сш – коэффициент Шези, м0,5с. Коэффициент Шези зависит от характера и состояния граничных поверхностей и режима движения жидкости. Эмпирическая зависимость, предложенная Н.Н. Павловским для расчета коэффициента Шези, имеет вид:
где n – коэффициент шероховатости, R – гидравлический радиус, показатель степени
или приближенно при R < 1м, у = n0,5, при R > 1м, у =1,3 n0,5. При наличии измеренных уклонов коэффициент Шези вычисляется из отношения (1.4.3):
При отсутствии данных об уклонах может быть использована формула Штриклера-Маннинга:
где dэ – эффективный диаметр, для условий рек. Определяемый как среднее значение крупности частиц по гранулометрической кривой. Параметр извилистости j выражается соотношением
где lфорв – длина участка, измеренная по фарватеру; lпр – длина этого же участка, измеренная по прямой. Местный уклон свободной поверхности воды характеризуется отношением
где dH – изменение уровня воды потока на его длине dL, а осредненной на длине L - отношением
где Н1 и Н2 – уровни воды (отметки) в точках, расстояние между которыми равно L. В гидравлике используется некоторая величина, называемая модулем расхода, она обозначается через К и определяется равенством
Модуль К имеет размерность расхода. Коэффициент турбулентного обмена, являющийся основным параметром при расчете перемешивания в потоках, вычисляется по формуле:
где g - удельный вес воды, кг/ м3; М вычисляется по формуле М = 0,7· Сш + 6, если Сш < 60, а при Сш > 60 величина М = 48 = const. Размерность М соответствует размерности коэффициента Шези. Размерность А – кг/м.с. В случае ярко выраженной неравномерности распределения на участке разбавления вводится поправочный множитель к коэффициенту турбулентного обмена А. Выбор зависимости для коэффициента турбулентной диффузии является основой для решения уравнений турбулентной диффузии. Определение значения и функциональной связи этого коэффициента для водоёмов и водотоков является самостоятельной задачей, выходящей за рамки настоящей работы [32]. Коэффициенты турбулентной диффузии рассчитываются по одной из полуэмпирических зависимостей, приведённых в табл. 2.3, выбираемых исходя из типа водного объекта, или принимаются по данным натурных исследований. Таблица 2.3 Формулы для определения коэффициента диффузии
При стационарном режиме процесса КДП и ПВ (например, впадение рек, попуски из водохранилищ, подземное питание, стационарный выпуск сточных вод) смешение создается поперечной и вертикальной турбулентной диффузией. Снижение концентраций, связанное с продольной дисперсией, является пренебрежимо малым [33]. Кроме гидравлических факторов на процесс трансформации качества воды в водоемах влияют химические и биохимические факторы. Интенсивность и характер физико-химических и биохимических процессов, в которые вовлекаются сточные воды при конвективно-диффузионном переносе, определяется степенью неконсервативности веществ. Наиболее разработанным в настоящее время является учет самоочищающей способности водотоков, связанной с превращением органических веществ, интенсивность которых характеризуется коэффициентом неконсервативности. Величина коэффициента биохимического разложения k1 зависит от ряда факторов (категория и нагрузка загрязнения, гидродинамические характеристики потока, температура воды и т.д.) и изменяется во времени. Это объясняется тем, что первыми вовлекаются в превращения наиболее легкоокисляемые вещества и остаются все более трудноокисляемые с меньшими коэффициентами неконсервативности. Несмотря на то, что каждое отдельное вещество может потребляться с постоянным кинетическим коэффициентом, общий коэффициент неконсервативности смеси будет уменьшаться. Существует ряд методов решения задач идентификации параметров математических моделей, рассмотрению которых посвящена обширная литература. Эти методы обычно подразделяются на прямые, иначе – методы обращения модели или решения, когда результаты наблюдений подставляются непосредственно в математическую модель, после чего посредством проведения различных преобразований выражают неизвестные параметры, и экстремальные, основывающиеся на том, чтобы при различных реализациях параметров рассматриваемого процесса, он был бы лучшим по некоторому априорно принятому критерию. Формулировка задач идентификации, решаемых экстремальными методами, должна включать, во-первых, уравнение, описывающее процесс (математическую модель исследуемого явления), во-вторых, критерий качества (целевую функцию, функционал). Кроме того, постановка задачи может содержать некоторые ограничения в виде равенств и неравенств, которые могут быть наложены на решение и искомые параметры модели с целью сохранения её физического смысла и улучшения вычислительных свойств задачи [34].
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 514; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.134.165 (0.008 с.) |

 (2.44)
(2.44) (2.45)
(2.45) (2.46)
(2.46)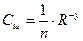 (2.47)
(2.47) (2.48)
(2.48) (2.49)
(2.49) (2.50)
(2.50) , (2.51)
, (2.51)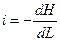 , (2.52)
, (2.52) , (2.53)
, (2.53)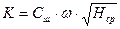 . (2.54)
. (2.54)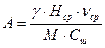 , (2.55)
, (2.55)