
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к практикумуСодержание книги
Поиск на нашем сайте
«Расчеты тепломассопереноса в реках и водоемах» Общие положения
Для практических расчетов разработаны разного рода схематизации задачи в виде частных моделей распространения неконсервативных примесей, солей и температуры. В основу решения этих моделей положены одномерные уравнения движения и неразрывности с применением операции осреднения по поперечным сечениям потока, к которым добавляются однотипные уравнения переноса тепла, кислорода и других субстанций. При решении задачи переноса основное внимание уделяется определению значений входящих в уравнения переноса коэффициентов диффузии. В частности, коэффициентов тепло - и температуропроводности или консервативности примеси. Вопрос определения этих коэффициентов затрудняется необходимостью исследования гидродинамики, например, требуется определение коэффициента турбулентной диффузии О.Ф. Васильев (1965, 1976) отмечает, что на достаточно большом расстоянии от места сброса тепла роль продольной дисперсии становится пренебрежительно малой, вследствие чего температура воды или концентрация примеси на этом расстоянии определяется главным образом адвективным переносом. Аналогичные выводы делал Д. Харлеман (1972) и др. Обычно принимается, что переносимое течением тепло не влияет существенным образом на плотность воды. Тогда в динамическом уравнении изменение плотности по длине водотока принимается равным нулю (так называемое баротропное приближение). В этом случае уравнения Сен-Веннана решаются независимо от остальных, и затем полученные результаты используются для решения уравнения переноса тепла. С помощью такого решения можно предсказывать распределение температуры воды вдоль водотока, основываясь на данных о поступавшем водном и тепловом стоке в верхнем створе водотока и теплообмена с окружающей средой. Пусть имеется информация о среднем установившемся уровне водоема
Рис.1. Принятая система координат.
Рассмотрим уравнение теплопроводности в заданных координатах в виде
Это уравнение получено в предложении, что перенос тепла в продольном направлении Х происходит, главным образом за счет течений,
а перенос тепла в вертикальном Z и поперечном Y направлении за счет турбулентной диффузии
Указание допущения в некоторой степени искажают истинную картину процесса теплопередачи, но в целом позволяют оценить основные физические закономерности. Например, первое допущение позволяет пренебречь турбулентным тепловым потоком в продольном направлении. Этот вопрос специально рассмотрен А.П. Пеховичем (1972). Второе допущение подтверждается анализом большого числа натурных наблюдений и является общепринятым. Третье допущение позволяет в некоторой степени учесть теплоперенос в поперечном направлении, которым обычно вовсе пренебрегают. Представление поперечных теплопотоков в виде правой части уравнения (8) является достаточно формальным. Коэффициенты
В реальных условиях тепловой поток обусловлен не только градиентом температуры, но и множеством других факторов, подчас вообще не поддающихся учету. Естественно, что в этих условиях величины Важным требованием к моделям естественных процессов является изменяемость всех входящих в них параметров. Величины
(13) где:
Рис.2 Уравнение (13) получено с помощью гипотезы (12). В это уравнение входят лишь величины, поддавшиеся непосредственному измерению ( В большинстве случаев исследователя интересует главным образом, пространственно-временная изменчивость среднего по сечению теплосодержания водотока Для замыкания уравнения (13) необходимо параметризировать профиль температуры по координате
Вид функций (14) может быть определен либо из непосредственных наблюдений, либо продиктован соображениями здравого смысла. Например, при простейшей параметризации вида
уравнение (13) принимает вид
Уравнение (16) необходимо дополнить краевыми условиями. Начальное условие задаем в виде
Выбор граничных условий для уравнения гиперболического типа определяется типом течения. Если
Если на нижнем створе имеет место инверсия потока
Система уравнений (13), (14), (17) - (19) является замкнутой. Такой подход может быть использован в системе уравнений движения и неразрывности или отдельно, когда известны значения V и Уравнение (13) является нелинейным благодаря нелинейной зависимости его правой части от температуры. Его решение возможно только численным методом. Условия однозначности Использование системы уравнений (13), (14), (17) - (19), записанных для отсека воды, при. расчете гидротермического режима всего водоема дает возможность переносить данные одного створа на другой, неизученный, и тем самым вести расчет изменения температуры воды по длине водоема (водотока), если известен теплообмен через грани отсека. Для решения системы уравнений необходимо знать условия однозначности, которые должны включать в себя: · граничные условия, которые выражают собой тепловое взаимодействие водной массы с окружающей средой (атмосферой и грунтом дна через водные границы); · начальные условия, т.е. распределение температуры по длине водоёма в момент времени, принимаемый за начальный;
· морфометрические условия, в частности глубину, ширину и длину отсека водоема; · теплофизические характеристики воды: теплоёмкость и объёмный вес воды. Наиболее просто назначить теплоёмкость и объёмный вес воды. Глубина и ширина участка назначаются исходя из морфометрии водоёма. Начальные условия можно принять по данным натуральных наблюдений или путём теплового расчёта за предыдущий период времени или задать приближенно, отнеся начальный момент времени в достаточно отдалённое время. Наиболее сложная задача – назначение граничных условий применительно к конкретному водоёму. Особенно трудно выполнить практические расчёты для малоизученных в гидрометеорологическом отношении водных объектов. Граничные условия по поверхности и дну отсека определяется не только метеоусловиями, но и зависит от температуры воды самого отсека. Поэтому при получении уравнения (13) они вошли в правую часть теплового баланса отсека. Использование (12) позволило в неявной форме учесть величину коэффициента теплопроводности. При задании граничных условий через боковую поверхность можно предполагать, что тепловой сток вполне определяется водным стоком. При этом боковая тепловая приточность вычисляется по формуле:
Основным критерием возможности практического решения уравнения (13) является выбор слагаемых теплового баланса поверхности водоёма, в основном определяющих его правую часть. Рассмотрим их. Если количество теплоты, поступающей извне в тело, известно (задано), то такое граничное условие называют ГУ второго (II) рода. Если же количество теплоты, поступающей в тело, выражается уравнением Ньютона Когда коэффициент теплоотдачи очень велик, температура поверхности оказывается заданной величиной, равной температуре окружающей среды, это представляет собой частный случай ГУ III рода Таким образом, имеем следующие выражения для ГУ: II рода III рода При контакте двух тел, вода-дно, вода-лёд, в которых теплота переносится лишь теплопроводностью, имеем ГУ IУ рода:
При наличии на поверхности тела слоя, имеющего очень высокую теплопроводность, например, слоя ветрового перемешивания в водохранилище, и заданного количества теплоты, поступающего в слой извне, имеем ГУ У рода:
Практически важным является ГУ IУ рода при наличии на границе источника (стока) теплоты, возникающего от изменения агрегатного состояния, например, при промерзании грунта:
где объёмная теплота фазового перехода равна:
m - пористость грунта; Возможны и некоторые другие ГУ: так, часто встречаются совмещения ГУ II и III родов, которое производится путём замены действительной температуры окружающей среды
где
Методы решения задач После того, как установлена цель, дана физическая и полная математическая формулировка задачи, следует выбрать метод её решения. Такова первоначальная последовательность работы, но необходимо иметь ввиду, что существует и обратная связь – выбор метода может побудить несколько, изменить формулировку задачи в сторону уточнения или, наоборот, огрубления схемы исследуемого природного явления или технического процесса. Основные методы решения задач тепломассопереноса следующие: а) аналитический, б) конечных разностей (графический, численный), в) моделирования (физического и математического), г) аналогий (электрической, гидравлической). Всякая задача имеет лишь одно решение, но форма решения может быть различной. Во всех случаях решение должно удовлетворять уравнению теплового баланса (УТБ) непосредственно для отсека (или уравнению теплопроводности УТБ) и краевым условиям. При использовании ЭЦВМ наиболее употребим метод конечных разностей. Метод состоит в том, что в УТБ, которое подлежит решить, все бесконечно малые разности (дифференциалы) заменяются конечными, но малыми разностными величинами. Таким образом, истинное непрерывное в пространстве распределение температуры и непрерывные во времени ход температуры заменяется приближёнными прерывистыми значениями, усредняющими температуры конечных малых участков тела Достоинства. Возможность решить весьма сложные задачи, в том числе с телами сложной формы, с переменными ГУ и теплофизическими характеристиками, с изменением агрегатного состояния и т.д. Рассмотрим возможности решения уравнения переноса с использованием ЭВМ. Уравнение (16) является квазилинейным из-за нелинейной зависимости его правой части от температуры. В настоящее время метод конечных разностей является единственным, позволяющим найти эффективное решение таких уравнений. При гидрологических расчётах с помощью (13) и (16) выбор конечно-разностной схемы решения имеет важное значение. Это обусловлено малой изученностью гидро- и термодинамики водотоков, отсутствием подробных гидрометеорологических данных наблюдений, а также сложностью реализации балансовых задач на ЭВМ. Уравнение (16) можно рассматривать как уравнение переноса:
(здесь Построим основную сеть Используем схему вида:
и примем
Полученная схема по форме записи соответствует физике процесса, так как в гидрофизических задачах обычно принимается, что
то есть правая часть уравнения (31) зависит от средней температуры по Рассмотрим частный случай. Пусть
Соответственно, схема (31) преобразуется в схему
Последняя решается методом итераций (подбором численного значения Интересно отметить, что схема (31) и использованная связь (32) совпадают с рекомендациями Б.А. Браславского (1964) для расчёта термического режима в проточном водоёме. Отличие в том, что схема (31) записана в более общем виде и выбор Для неподвижного водоёма Д.И. Бибиковым и Н.Н. Петруничевым (1950) приведена графоаналитическая схема решения уравнения (34). В её основе лежит связь (38), так как решение ищется как среднее за период Очевидно, что система (31) – (32) является наиболее общим вариантом решения прикладной задачи теплопереноса. Однако часто пользуются (рис. 3) уравнением теплового баланса для отсека
Рис. 3. Схема теплопотоков на границах водного отсека.
Уравнение (36) для расчёта термического режима водотока используется в конечно-разностной форме (39). Последняя связывает среднюю начальную и конечную температуру отсека воды за период
а также связь средней по объёму температуры воды с конечной и начальной температурой
Тогда система
где Уравнение (39) позволяет выполнять расчёты термического режима водоёмов, но не чувствительность к изменению уровня по длине водотока и во времени снижает точность результатов. В отличие от (39) в формулах (13) и (16) учитывается распределение температуры воды по сечению с использованием информаций об изменениях морфометрических условий и не стационарности движения воды. Кроме того, эти уравнения идеально приспособлены для реализации на ЭВМ.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.122.145 (0.013 с.) |

 и его ширине
и его ширине  при отсутствии паводка. Для верхнего створа исследуемого объекта этот уровень можно принять за начало координат. Введем ось X, направленную вдоль оси водотока, ось Z направим вниз, а ось Y направим перпендикулярно плоскости XOZ c началом на оси водотока.
при отсутствии паводка. Для верхнего створа исследуемого объекта этот уровень можно принять за начало координат. Введем ось X, направленную вдоль оси водотока, ось Z направим вниз, а ось Y направим перпендикулярно плоскости XOZ c началом на оси водотока.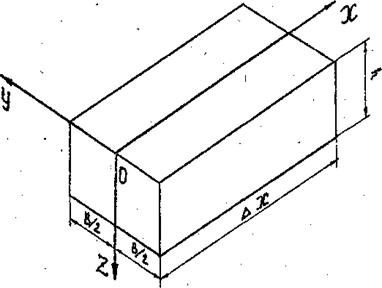
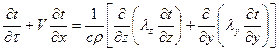 (8)
(8) (9)
(9)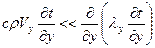 (10)
(10)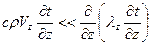 (11)
(11)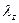 и
и 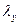 имеют смысл некоторых эффективных коэффициентов теплопроводности, хотя с физической точки зрения ничего общего с коэффициентами теплопроводности они не имеют. Однако с их помощью записывается общепринятая гипотеза о пропорциональности потока тепла
имеют смысл некоторых эффективных коэффициентов теплопроводности, хотя с физической точки зрения ничего общего с коэффициентами теплопроводности они не имеют. Однако с их помощью записывается общепринятая гипотеза о пропорциональности потока тепла  градиенту температуры:
градиенту температуры: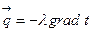 (12)
(12) . Результат интегрирования можно представить в следующем виде
. Результат интегрирования можно представить в следующем виде
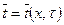 - средняя по поперечному сечению температура воды;
- средняя по поперечному сечению температура воды; 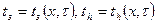 - средние температуры поверхности и дна;
- средние температуры поверхности и дна;  и
и 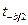 - температура на правом и левом берегу;
- температура на правом и левом берегу; 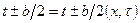 ;
; 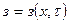 - превышения уровня воды над равновесным;
- превышения уровня воды над равновесным; 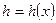 невозмущенная глубина потока (рис.2);
невозмущенная глубина потока (рис.2); 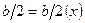 - полуширина потока (ось
- полуширина потока (ось  направлена вдоль осевой линии потока);
направлена вдоль осевой линии потока); 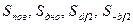 - величины удельных теплопотоков через горизонтальную, нижнюю, боковые поверхности водотока;
- величины удельных теплопотоков через горизонтальную, нижнюю, боковые поверхности водотока; 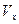 - средняя скорость потока на сечении вдоль оси Х;
- средняя скорость потока на сечении вдоль оси Х;  - удельная теплоемкость воды;
- удельная теплоемкость воды; 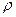 - плотность воды. Величины
- плотность воды. Величины 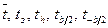 ), либо величины, значения которые могут быть вычислены с помощью надежных эмпирических формул (
), либо величины, значения которые могут быть вычислены с помощью надежных эмпирических формул (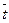 и температура его поверхности
и температура его поверхности 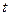 . Поэтому, несмотря на то, что уравнение (13) является менее информативным по сравнению с уравнением (8), его точность является достаточной для практических расчетов. В методическом плане оно выгодно отличается (6) отсутствием не поддающихся определению величин
. Поэтому, несмотря на то, что уравнение (13) является менее информативным по сравнению с уравнением (8), его точность является достаточной для практических расчетов. В методическом плане оно выгодно отличается (6) отсутствием не поддающихся определению величин  и
и  . Запишем эту параметризацию в общем виде:
. Запишем эту параметризацию в общем виде: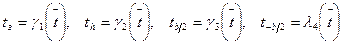 (14)
(14)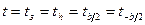 (15)
(15)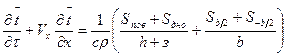 (16)
(16)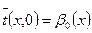 (17)
(17)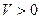 для всех
для всех 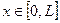 , где
, где 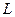 - длина участка интегрирования, то достаточно задать условие, лишь на верхнем створе:
- длина участка интегрирования, то достаточно задать условие, лишь на верхнем створе: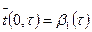 (18)
(18)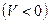 , что может наблюдаться при прохождении нагонных волн, необходимо задать также условие на нижнем створе:
, что может наблюдаться при прохождении нагонных волн, необходимо задать также условие на нижнем створе: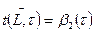 (19)
(19) . Кроме того, при достаточно малой скорости V или при её отсутствии уравнение (13) позволяет рассчитать термический режим водоема с учетом колебания уровня относительно некоторой глубины по заданным
. Кроме того, при достаточно малой скорости V или при её отсутствии уравнение (13) позволяет рассчитать термический режим водоема с учетом колебания уровня относительно некоторой глубины по заданным 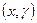 .
.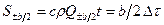 (20)
(20) , то имеет место ГУ третьего (III) рода.
, то имеет место ГУ третьего (III) рода.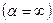 , который является наиболее простым и называется ГУ I рода.
, который является наиболее простым и называется ГУ I рода. (21)
(21) (22)
(22)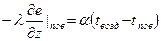 (23)
(23)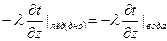 (24)
(24)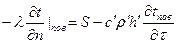 (25)
(25) (26)
(26) (27)
(27)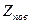 - координата фазового перехода.
- координата фазового перехода.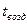 эквивалентным значением
эквивалентным значением 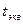 :
: (28)
(28)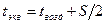 (29)
(29) и малых промежутков времени
и малых промежутков времени 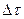 .
.
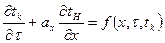 (30)
(30)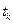 и
и 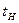 - конечная и начальная температура), для которого формулируется краевая задача, когда при
- конечная и начальная температура), для которого формулируется краевая задача, когда при 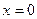 задаю граничное значение
задаю граничное значение  , и решение ищется при
, и решение ищется при 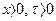 , При
, При 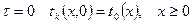 , причём
, причём 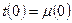 .
.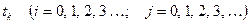 с постоянными шагами
с постоянными шагами  и
и 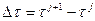 . Обозначим эту сеть
. Обозначим эту сеть 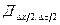 , введём в рассмотрение сеть
, введём в рассмотрение сеть 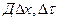 добавлением к ней узловых точек
добавлением к ней узловых точек 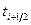 и
и 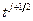 , совпадающих с серединами интервалов
, совпадающих с серединами интервалов 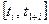 и
и 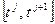 .
. (31)
(31)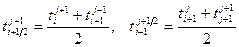
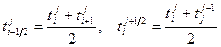 (32)
(32) , (33)
, (33) и
и 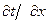 = 0 или V=0, тогда из (30) получаем
= 0 или V=0, тогда из (30) получаем . (34)
. (34) . (35)
. (35) , входящего в правую и левую части уравнения (30)).
, входящего в правую и левую части уравнения (30)).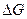 . Там же рассмотрен пример решения задачи проектирования распределения температуры по длине водотока. В основу предлагаемого способа положено уравнение (16) при допущениях(37) и при пренебрежении первым членом уравнения (16).
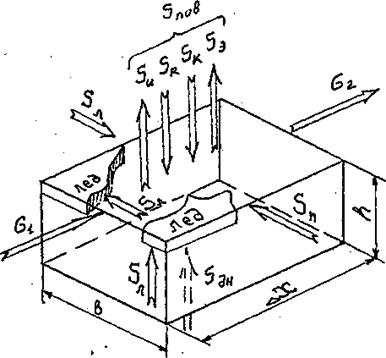
. Там же рассмотрен пример решения задачи проектирования распределения температуры по длине водотока. В основу предлагаемого способа положено уравнение (16) при допущениях(37) и при пренебрежении первым членом уравнения (16).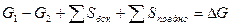 (36)
(36)
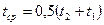 (37)
(37)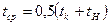 . (38)
. (38) и уравнение (36) запишутся следующим образом:
и уравнение (36) запишутся следующим образом: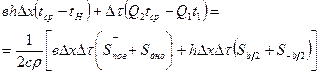 (39)
(39)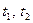 - средняя температура верхнего и нижнего створов;
- средняя температура верхнего и нижнего створов; 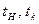 - средние значения начальной и конечной температуры отсека;
- средние значения начальной и конечной температуры отсека; 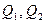 - расходы воды через верхний и нижний створы. Рассматривая слагаемые, выражающие адвективный перенос тепла, можно предположить, что
- расходы воды через верхний и нижний створы. Рассматривая слагаемые, выражающие адвективный перенос тепла, можно предположить, что 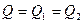 , тогда произведение
, тогда произведение 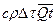 , представляет собой тепловой приток
, представляет собой тепловой приток 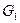 и сток
и сток 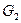 с рассматриваемого участка с размерами
с рассматриваемого участка с размерами 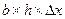 .
.


