Имитационное моделирование задач формирования качества воды при различных видах техногенной нагрузки

Основной особенностью имитационного моделирования различных типов задач КДП и ПВ являются многовариантные эксперименты с численным изменением краевых условий (начальных и граничных). Целью моделирования в большинстве случаев является предсказать качество воды в водном объекте на определённом расстоянии от того или иного источника сброса сточных вод, то есть в контрольном створе.

 

Принципы моделирования

 

Имитационное моделирование базируется на основных принципах моделирования, в сжатой форме отражающих большой опыт, накопленный к настоящему времени в области разработки и использования математических моделей, которые приведены ниже.

 

Принцип информационной достаточности.

При полном отсутствии информации об исследуемой системе построение её модели невозможно. При наличии полной информации о системе её моделирование лишено смысла. Существует некоторый критический уровень априорных сведений о системе (уровень информационной достаточности), при достижении которого может быть построена её адекватная модель.

 

Принцип осуществимости.

Создаваемая модель должна обеспечивать достижение поставленной цели исследования с вероятностью, существенно отличающейся от нуля, и за конечное время. Обычно задают некоторое пороговое значение Р0 вероятности достижения цели моделирования Р(t), а также приемлемую границу t0 времени достижения этой цели. Модель считают осуществимой, если может быть выполнено условие Р(t0) ³ P0.

Принцип множественности моделей.

Данный принцип является ключевым. Речь идёт о том, что создаваемая модель должна отражать в первую очередь те свойства реальной системы (или явления), которые влияют на выбранный показатель эффективности. Соответственно при использовании любой конкретной модели познаются лишь некоторые стороны реальности. Для более полного её исследования необходим ряд моделей, позволяющих с разных сторон и с разной степенью детальности отражать рассматриваемый процесс.

 

Принцип агрегирования.

В большинстве случаев сложную систему можно представить состоящей из агрегатов (подсистем), для адекватного математического описания которых оказываются пригодными некоторые стандартные математические схемы. Принцип агрегирования позволяет, кроме того, достаточно гибко перестраивать модель в зависимости от задач исследования.

 

Принцип параметризации.

В ряде случаев моделируемая система имеет в своём составе некоторые относительно изолированные подсистемы, характеризующиеся определённым параметром, в том числе векторным. Такие подсистемы можно заменять в модели соответствующими числовыми величинами, а не описывать процесс их функционирования. При необходимости зависимость значений этих величин от ситуации может задаваться в виде таблицы, графика или аналитического выражения (формулы). Принцип параметризации позволяет сократить объём и продолжительность моделирования. Однако надо иметь в виду, что параметризация снижает адекватность модели. [21,23]

Конечной целью любой имитационной модели является описать и предсказать ответную реакцию водной среды на ту или иную форму воздействия. При этом схема реакции является результатом достаточно большого числа процессов, которые протекают в среде. Операциями являются следующие процессы, которые часто описываются самостоятельной подмоделью.

1. Перенос вещества и разбавление сточных вод. Для описания этих процессов требуются данные по гидрологии и гидродинамике водных объектов; анализ течений, турбулентной диффузии и т.д.

2. Осаждение трудно разложимых примесей, вторичное загрязнение. Эти вопросы, как правело, требуют специальных экспериментальных исследований.

3. Распад легко разложимых примесей, самоочищение водной среды. Хронологически, первым описанием этих процессов были уравнения Ф-С, включающие в себя две переменные: качество БПК и растворённый кислород. Причем уравнения линейны по данным переменным и модель Ф-С не учитывает в должной мере динамики водных систем, ответственных за процессы разложения. В настоящее время в инженерной практике используют бимолекулярную модель и более сложные модели процессов самоочищения, включающие в качестве переменных различные трофические уровни экосистем.

4. Термическое загрязнение. В качестве анализа гидрологического и гидродинамического объекта. Исследование термического режима объекта имеет не только самостоятельное значение. Поскольку, интенсивность жизненных процессов существенно зависит от температуры, адекватное описание процессов самоочищения водной среды невозможно без учета температурного режима. В инженерной практике исследование поведения динамических кривых растворенного кислорода, фосфора в зависимости от интенсивности термических загрязнений и величин БПК. Часто при решении инженерных задач помимо БПК и растворенного кислорода в моделях рассматриваются профили концентраций хлоридов, аммиака, взвешенных частиц и множество других показателей, в зависимости от термических загрязнений [23].

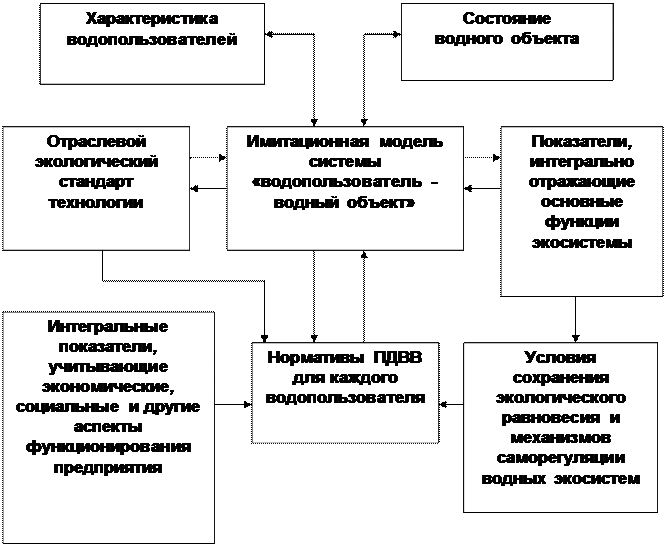
В соответствии с современными положениями о нормировании техногенной нагрузки в рамках данной работы предполагается основное внимание уделить п. 1, то есть прогнозу переноса вещества и разбавления сточных вод.

Для расчётов разбавления сточных вод в реках и водоёмах в качестве основных должны рассматриваться методы, основанные на использовании численных решений уравнений турбулентной диффузии. Различают детальные и упрощённые методы. Детальные методы расчёта представляют собой непосредственные решения уравнений, а упрощённые – строятся на аналитической или графической аппроксимации этих решений.

Математическое прогнозирование в соответствии с рисунком 2.5 заключается в использовании имеющейся информации об объекте прогнозирования, обработке этой информации математическими методами, получении зависимости связывающей эти характеристики со временем или с некоторыми другими независимыми переменными и вычислении характеристик объекта в заданный момент времени при заданных значениях других независимых переменных. Нахождение закономерности в поведении прогнозируемого объекта позволяет построить его математическую модель, которая вследствие явления изоморфизма позволяет исследовать реальные физические процессы путем их математического моделирования. Одинаковые по форме математические выражения при различном физическом содержании входящих в них символов получили название «изоморфные» [3].

На рис. 2.6 представлена схема, показывающая связь и место имитационной модели в общей системе «водопользователь - водный объект – модель - экологические нормативы». На основании условий сохранения экологического равновесия в водном объекте и с учётом механизмов саморегуляции водных экосистем, а также всех аспектов функционирования предприятий-водопользователей, определяются нормативы ПДВВ, согласующиеся с экологическими стандартами. В соответствии с типом водного объекта и поставленными целями составляется расчётная схема, в соответствии с которой строится имитационная модель. На основании экологических стандартов и показателей, отражающих основные функции экосистемы, характеристик водопользователей и параметров водного объекта задаются начальные и граничные условия, определяются параметры модели. В соответствии с расчётом по построенной модели определяются допустимые нормативы сброса и, соответственно, необходимые мероприятия по улучшению технологий и т. п. водопользователей.

 

 

Рис. 2.5. Структурная блок-схема прогнозирования

Где: ---------------- вычислительные операции; ¾¾¾¾¾¾ исследовательские операции.

Современная методология оценки предельно-допустимых вредных воздействий (ПДВВ) на водный бассейн или его часть вызвала необходимость разработки и внедрения технических и программных средств нового поколения. Эти средства в соответствии с постановкой задачи математического моделирования переноса и превращения загрязняющих веществ должны реализовать не только переменные гидролого-морфологические, гидродинамические характеристики на отдельных участках водного бассейна, но и все имеющиеся сосредоточенные и диффузные источники загрязнения, а также естественные притоки. Основные блоки данной системы представлены на рисунке 2.6.

Решить такого рода задачи возможно с использованием современных средств имитационного схемотехнического моделирования речного бассейна. Основные принципы и элементы программного обеспечения описаны в ряде работ [24, 25]. В качестве теоретических основ имитационного схемотехнического моделирования речного бассейна и построения типовых расчётных моделей использованы работы [5, 6, 16, 19, 26].

 

Пример постановки задачи формирования качества воды (модели распространения загрязнений в основном русле р. Невы)

 

В общем случае всегда присутствует необходимость в разработке методики моделирования водного бассейна с учётом естественных и техногенных факторов и взаимовлияния источников сброса сточных вод. При этом особое внимание необходимо уделить выбору и адаптации математических моделей в соответствии с исследуемым объектом и разработке программно-технических средств их практической реализации.

Поэтому можно сформулировать следующие этапы работы:

Разработка методики и алгоритма имитационного моделирования речного бассейна на основе бассейнового подхода.

Разработка специализированных схемотехнических средств реализации типовых моделей КДП и ПВ, начальных и граничных условий.

Разработка методики оценки предельно-допустимых вредных воздействий (ПДВВ) на водные объекты и алгоритма перераспределения нагрузки в речном бассейне на основе методов и средств схемотехнического моделирования.

 

5.4.1. Гидрологическая оценка объекта исследования (реки Нева)