
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 3. Расчёт среднедневного и среднедекадного значения коэффициента теплопроводности для слоя снега при постоянной его плотностиСодержание книги
Поиск на нашем сайте
Постановка задачи Расчёт коэффициента теплопроводности снега производится исходя из зависимости плотности снега от температуры воздуха на поверхности снегового покрова. Тогда коэффициент теплопроводности снега
где
За декаду амплитуда колебаний температуры воздуха должна быть более 10 Задача решается (рис. 7) аналогично предыдущей (50) методом сеток, изложенным выше. Решением является неизвестная величина температуры снега в его слое. Граничные условия – температура подстилающей поверхности, температура воздуха на поверхности снегового покрова. Начальные условия – распределение температуры по глубине в первый день наблюдений.
Со стр 25
Рис. 7
Их соотношения определяются из (54). Таким образом, решение задачи сводится к следующему: 1. Расчёт методом сеток недостающих частей 2. Нахождение для каждой 3. Расчёт среднего Ограничения: Точность метода: известно, что свежевыпавший снег с плотностью При решении задачи использовались следующие значения Очевидно, что метод себя оправдывает, сохраняя общие тенденции изменения теплопроводности в зависимости от температуры. Пример решения В исходные данные входят два массива по 50 величин в каждом, что соответствует значениям температуры и теплопроводности для пяти глубин снега и десяти дней наблюдений, и константы плотности, которая при необходимости может быть заменена массивом (если происходит изменение плотности во времени и по глубине). Данные вводятся с терминала и выводятся на АЦПУ в виде таблицы:
(здесь должна быть таблица) со стр 26
7.4.4. Задача 4. Расчёт разбавления сточных вод в реках по методу А.В. Караушева (плоская задача) Постановка задачи Метод, основанный на численном решении уравнения турбулентной диффузии, позволяет получать поле концентрации загрязняющего вещества в пределах всей расчётной области, начиная от источника загрязнения до створа водопользования. Для условий плоской задачи при пренебрежимо малых поперечных скоростях и стационарного во времени процесса уравнение турбулентной диффузии в конечных разностях примет вид (5):
При расчёте поток в плане разбивается сеткой, каждая вертикальная линия которой отвечает определённому поперечному сечению и предполагается отстоящей от предыдущей и последующей на длине Расстояние между горизонтальными линиями (по ширине реки) равно На рис. 8 изображена сетка к расчёту турбулентной диффузии (плоская задача).
(здесь должна быть таблица)со стр 28
Рис. 8 Расчётная зависимость, позволяющая вычислить распределение концентраций загрязняющих веществ по длине и ширине потока (плановая или иначе плоская задача), записывается аналогично (41)-(46), т.е.
При расчёте по уравнению (56) вся изучаемая область потока или водоёма делится на прямоугольные параллелепипеды, объёмы которых равны Расстояние между расчётными сечениями определяются по формуле
Когда раствор загрязняющего вещества достигает граничных поверхностей потока, для расчёта диффузии следует использовать соотношение, учитывающее отсутствие переноса через стенки потока:
Учёт граничных условий осуществляется путём введения в расчёты экстраполяционных значений концентрации. Расчётная сетка и поле концентрации условно распространяется за ограничивающие поток поверхности. При этом экстраполяционные значения концентрации в клетке, примыкающей к внешней поверхности стенки
где Начальные условия учитываются при задании места выпуска сточных вод, их расхода Вычисляется условная площадь поперечного сечения притока
Затем определяется ширина загрязнённой струи в начальном створе:
В соответствии с величиной Клетки, попадающие в струю притока сточных вод в начальном поперечнике, заполняются цифрами, выражающими начальную концентрацию сточных вод Часто оказывается удобным вести вычисления в относительных величинах концентрации, например, в % от Пример решения Исходные даны: Река … является приёмником сточных вод населённого пункта. Объём сточных вод Благополучное санитарное состояние реки обеспечивается при 20-кратном разбавлении сточных вод Расход реки
Требуется определить значение максимальной концентрации загрязняющих веществ в нижерасположенном населённом пункте (на расстоянии
Ход выполнения работы 1. Определяем величину расчетного расхода в реке:
2. Находим начальное сечение струи загрязнения
3. Вычисляем ширину загрязнённой части реки в начальном сечении
4. Назначаем ширину расчётной клетки
Общее число клеток по ширине реки 5. Расстояние между расчётными сечениями
Разбив сетку в соответствии с полученными значениями Примечания: а) В каждом расчётном сечении следует проверять сумму концентраций, поступивших загрязняющих веществ б) Если значения Концентрация загрязняющего вещества в укрупнённых клетках вычисляются как среднее арифметическое из концентраций в объединяемых клетках.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 448; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.105.184 (0.009 с.) |

 можно рассчитать по следующим формулам:
можно рассчитать по следующим формулам:


 – плотность снега;
– плотность снега; 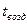 – температура воздуха,
– температура воздуха, 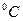 . Для упрощения задачи плотность может быть выбрана постоянной и задача сводится к нахождению величины
. Для упрощения задачи плотность может быть выбрана постоянной и задача сводится к нахождению величины  для каждой точки снегового покрова в течение определённого промежутка времени с последующим нахождением среднего значения
для каждой точки снегового покрова в течение определённого промежутка времени с последующим нахождением среднего значения 
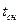 .
. имеет
имеет 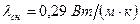 .
.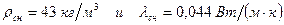 .
. . (55)
. (55) .
. . Каждой клетке присвоен свой индекс по соответствующим осям координат: по оси
. Каждой клетке присвоен свой индекс по соответствующим осям координат: по оси  - индекс
- индекс 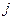 , по оси
, по оси  - индекс
- индекс  .
.
 (56)
(56) ,
,  – средняя глубина в рассматриваемой области. При пользовании этими формулами предполагается, что уже вблизи от выпуска сточные воды равномерно распространяются по всей глубине
– средняя глубина в рассматриваемой области. При пользовании этими формулами предполагается, что уже вблизи от выпуска сточные воды равномерно распространяются по всей глубине 
 (57)
(57) (58)
(58) (рис. 8), и значения концентрации
(рис. 8), и значения концентрации 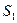 в клетке, примыкающей к внутренней поверхности стенки на том же поперечнике, должны удовлетворять условию (57), при решении плоской задачи, что возможно только в случае, если:
в клетке, примыкающей к внутренней поверхности стенки на том же поперечнике, должны удовлетворять условию (57), при решении плоской задачи, что возможно только в случае, если: (59)
(59) и их концентрации
и их концентрации 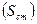 . На плане реки (или водоёма) обозначают место сброса и через него проводят начальный поперечник. Ниже по течению поток схематизируется и делится на расчётные клетки. Скорость сточных вод
. На плане реки (или водоёма) обозначают место сброса и через него проводят начальный поперечник. Ниже по течению поток схематизируется и делится на расчётные клетки. Скорость сточных вод 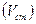 , сбрасываемых в водный объект, в месте их поступления принимается равной скорости течения реки
, сбрасываемых в водный объект, в месте их поступления принимается равной скорости течения реки  .
. в месте его падения по следующей зависимости:
в месте его падения по следующей зависимости: (60)
(60) (61)
(61) называется ширина расчётной клетки
называется ширина расчётной клетки  , однако если значения оказываются очень большими, то их уменьшают так, чтобы выполнялось неравенство
, однако если значения оказываются очень большими, то их уменьшают так, чтобы выполнялось неравенство  (В - средняя ширина реки).
(В - средняя ширина реки). (в частном случае это может быть нулевая концентрация).
(в частном случае это может быть нулевая концентрация).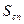 , полагая
, полагая  . Такой пример позволяет использовать данные расчёта для оценки распределения в потоке любого числа загрязняющих ингредиентов, если будут заданы исходные содержания последних в сточных водах.
. Такой пример позволяет использовать данные расчёта для оценки распределения в потоке любого числа загрязняющих ингредиентов, если будут заданы исходные содержания последних в сточных водах. . Сточные воды поступают через береговой коллектор. В меженные периоды возникают опасность загрязнения реки на участке, превышающем расстояние до нижерасположенного посёлка.
. Сточные воды поступают через береговой коллектор. В меженные периоды возникают опасность загрязнения реки на участке, превышающем расстояние до нижерасположенного посёлка. . Определить будет ли обеспечиваться данное условие, если посёлок расположен в …
. Определить будет ли обеспечиваться данное условие, если посёлок расположен в …  ниже по течению.
ниже по течению.

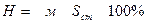

 от коллектора).
от коллектора).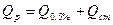

 по формуле (61):
по формуле (61):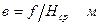
 :
:
 , равно
, равно  .
. находится из равенства
находится из равенства  .
. определяется по формуле (57):
определяется по формуле (57):
 и заполнив часть клеток концентрацией 100%
и заполнив часть клеток концентрацией 100%  , а остальные клетки нулевыми концентрациями, выполняем расчёт турбулентной диффузии по формуле (56) до створа, удалённого от места сброса на
, а остальные клетки нулевыми концентрациями, выполняем расчёт турбулентной диффузии по формуле (56) до створа, удалённого от места сброса на  .
. , что приводит к укрупнению величин
, что приводит к укрупнению величин  .
.


