Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие принципы моделированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Моделирование – это разработка, исследование модели и распространение модельной информации на оригинал. Достоинства моделирования проявляются там, где возможности традиционного подхода оказываются ограниченными. Именно такой областью познания является экология. Методы математического моделирования широко используются при исследовании экосистем. Модель должна соответствовать двум требованиям: - она должна отражать лишь те особенности оригинала, которые выступают в качестве предмета познания; - она должна быть адекватна оригиналу (иначе представления о нем будут искажены). Адекватность модели реальной экосистеме по критериям адекватности должна быть доказана до того, как исследователь проводит на модели эксперименты по изменению внешней и внутренней нагрузки на водоем. Моделирование сложных систем основано на некоторых основных принципах, к которым относятся: 1. Принцип информационной достаточности - моделирование не имеет смысла, если известно все о моделируемом объекте, но моделирование невозможно, если известно слишком мало, информации должно быть достаточно для моделирования; 2. Принцип осуществимости - модель должна обеспечивать достижение поставленной цели исследования с вероятностью, существенно отличающейся от нуля, и за конечное время; 3. Принцип множественности моделей - один и тот же объект может быть смоделирован разными способами, в разных его моделях главное внимание будет уделять разным сторонам моделируемого объекта, будет использоваться разный набор исходных характеристик; 4. Принцип агрегирования - представление сложной системы состоящей из агрегатов (подсистем), для адекватного математического описания которых могут быть использованы стандартные математические схемы; 5. Принцип параметризации - моделируемая система может иметь в своём составе некоторые относительно изолированные подсистемы, характеризующиеся определённым параметром, в том числе векторным, которые можно заменять в модели соответствующими числовыми величинами, а не описывать процесс их функционирования, что облегчает моделирование, но снижает адекватность модели; 6. Принцип иерархической организации - представление многообразия окружающей природы в виде соподчиненных друг другу естественных и искусственных систем; 7. Принцип несовместимости - чем глубже анализируется реальная сложная система, тем менее определенны наши суждения о ее поведении. Иными словами, сложность системы и точность, с которой ее можно анализировать, связаны обратной зависимостью; 8. Принцип контринтуитивного поведения сложной системы - невозможно дать удовлетворительный прогноз о поведении сложной системы на достаточно большом промежутке времени, опираясь только на собственный опыт и интуицию; наша интуиция «воспитана» на общении с простыми системами, где связи элементов практически всегда удается проследить, и контринтуитивность поведения сложной системы состоит в том, что она реагирует на воздействия совсем иным образом, чем это нами интуитивно ожидалось. Специалисты по теории принятия коллективных решений (Ворощук, 1982) также выдвигают ряд важных принципов, называя их принципами системности, которые необходимо соблюдать при построении имитационных систем, например: - требование непротиворечивости критериев исследования запрещает навязывать противоречивые условия развития процесса в системных исследованиях; - вводимая совокупность модельных параметров должна быть одновременно установлена количественно, должна иметься возможность синхронного установления величин параметров в определенные моменты времени; - введенные параметры должны иметь смысл на всем рассматриваемом пространстве и этот смысл должен оставаться неизменным в ходе всего процесса исследования; - принцип консервативности (проверка законов сохранения вещества в модели); и др.
Сущность метода моделирования состоит в том, что наряду с системой (оригиналом), которую мы обозначим через Ψ0 = Ψ0(V0, X0, ∑0, F0), рассматривается ее модель, в качестве которой выступает некоторая другая система - Ψ = Ψ (V, X, ∑, F), представляющая собой образ (подобие) оригинала S0 при моделирующем отображении (соответствии подобия) f, что принято обозначать записью
f: (Ψ0) → Ψ,
где скобки обозначают, что f- частично определенное отображение, т.е. не все черты состава и структуры оригинала отражаются моделью. Моделирующее отображение f целесообразно представить в виде композиции (продукта последовательного выполнения) двух отображений - огрубляющего g и гоморфного h:
g: (Ψ0) → Ψ1 ; h: Ψ1 → Ψ; f = h • g: (Ψ0) → Ψ, где Ψ1 = Ψ1(V1, X1, ∑1, F1) - некоторая подсистема системы Ψ0 , т.е. V1
Модель, как правило, представляет собой упрощенный образ оригинала, и это упрощение (огрубление) осуществляется отображением g,- при котором, сознательно удаляя из системы Ψ0 некоторые элементы и связи, мы получаем подсистему Ψ1. С другой стороны, модель должна в определенном смысле верно отражать оригинал,
Сначала огрубляющее отображение g: (Ψ0) → Ψ1 выделяет в системе Ψ0 ее подсистему Ψ1 с меньшим числом элементов и связей между ними, а затем отображение h: Ψ1 → Ψ гомоморфно переводит подсистему Ψ1 в модель Ψ. I - Ψ0(V0, X0, ∑0, F0); II - Ψ1(V1, X1, ∑1, F1); III - Ψ (V, X, ∑, F).
хотя возможно и огрубленно, или, как принято говорить в системном анализе, агрегированно. Именно это и осуществляет гомоморфное отображение подсистемы Ψ1 на модель Ψ. При этом может произойти дальнейшее огрубление, т. е. число элементов связей в модели Ψ может стать меньше, чем в Ψ1, а тем более в Ψ0 однако при этом не происходит искажения структуры, т. е. если некоторые элементы системы Ψ1 были связаны некоторыми отношениями, то их образы в модели Ψ должны быть связаны образом этого же отношения. Для пояснения понятия модели обратимся к рис. IV. 5, на котором изображена система-оригинал Ψ0 = Ψ0(V0, X0, ∑0, F0), внешняя среда которой V0 образована тремя элементами - причем
Следующее отображение h сливает элементы Нетрудно убедиться в том, что отображение h является гомоморфным. Действительно, взяв, например, элементы В зависимости от характера огрубления и степеням агрегирования для одного и того же оригинала можно получить несколько различных моделей. Стратегия моделирования заключается в попытке путем упрощения получить модель, свойства и поведение которой можно было бы эффективно изучать, но которая в то же время оставалась бы достаточно сходной с оригиналом, чтобы результаты этого изучения все же были применимы и к оригиналу. Обратный переход от модели Ψ к оригиналу Ψ0 называется интерпретацией модели. Процедура интерпретации не является строго однозначной, так как прообраз некоторых элементов или отношений модели в силу необратимости гомоморфного отображения h, при котором допустимо слияние элементов, может состоять из нескольких элементов или отношений системы-оригинала. Обычно оригинал Ψ0 представляет собой достаточно сложную систему, непосредственное установление закона функционирования которой Ψ0 сопряжено с большими трудностями. В то же время для некоторой ее модели Ψ ввиду ее относительно большей простоты функция Ψ0 может быть найдена тем или иным путем. После этого исследование системы Ψ0 можно заменить исследованиями ее модели Ψ, а затем интерпретировать полученные результаты применительно к системе - оригиналу Ψ0. Таким образом, при помощи моделирования в некотором приближении, определяемом степенью близости модели к оригиналу, может быть решена задача установления функции изучаемой сложной системы Ψ0. Оригинал и модель, а также разные модели одного и того же оригинала могут отличаться по своей реализации, где под реализацией понимается характеристика того, «из чего и как модель сделана» (Полетаев, 1966). Одно из достоинств метода моделирования состоит в возможности построения моделей с «удобной реализацией, ибо удачный выбор реализации делает исследование модели несравненно более легким, чем исследование оригинала, и в то же время позволяет сохранить существенные черты его состава, структуры и функционирования. В зависимости от особенностей системы - оригинала и задач исследования применяются самые разнообразные модели, которые целесообразно классифицировать по следующим признакам (рис.IV.6).
Рис. IV.6. Схематическая классификация моделей
По типу реализации различаются реальные и знаковые модели. Реальная модель отражает существенные черты оригинала уже по самой природе своей физической реализации. Например, аквариум с его растительностью, животным и микробным населением воспроизводит некоторые черты обитаемых природных водоемов уже потому, что он сам является населенным водоемом, хотя и значительно меньших размеров. Одна из наиболее сложных проблем, с которой приходится сталкиваться при работе с реальными (натурными) моделями, заключается в трудности установления степени адекватности модели оригиналу и, следовательно, в обосновании возможности применения результатов моделирования к исходной системе - оригиналу. В отличие, например, от аэро- или гидродинамики, где разработаны количественные критерии адекватности моделей (критерий Рeйнольдса и т. п.), в результате чего стало возможным успешное применение натурных моделей для решения широкого круга научных и конструкторских задач в указанных областях, при натурном моделировании экосистем вопросы обоснования адекватности еще очень далеки от удовлетворительного решения, на что уже указывалось выше при обсуждении значения лабораторных экспериментов. Кроме того, создание и использование натурных моделей экосистем связано с известными трудностями технического характера, преодоление которых, из-за отсутствия гарантий адекватности, отнюдь не всегда приводит к решению поставленной задачи. Знаковая модель представляет собой условное описание системы-оригинала с помощью данного алфавита символов и операций над символами, в результате чего получатся слова и предложения некоторого языка, которые с помощью определенного кода интерпретируются как образы некоторых свойств элементов системы-оригинала и связей между ними. Как отмечает И. А. Полетаев (1966), знаковые модели несравненно богаче возможностями, чем реальные, ибо они почти не связаны ограничениями физической реализации. Наибольшее значение для экологии имеют две разновидности знаковых моделей: это, во-первых, так называемые концептуальные и, во-вторых, математические модели. Концептуальная модель представляет собой несколько более формализованный и систематизированный вариант традиционного естественнонаучного описания изучаемой экосистемы, состоящей из научного текста, сопровождаемого блок-схемой системы, таблицами, графиками и прочим иллюстративным материалом. Несколько тавтологичный, но широко применяемый термин «концептуальная модель» подчеркивает, что назначение этой модели - служить ясным, обобщенным и в то же время достаточно полным выражением знаний и представлений исследователя об изучаемой системе в рамках и средствами определенной научной концепции. Например, в рамках «энергетической» или «биогеохимической» концепции соответствующие концептуальные модели принимают форму блок-схем трофических связей или потоков вещества в экосистеме, которые сопровождаются поясняющим текстовым, табличным и графическим материалом, раскрывают состав, структуру и некоторые аспекты функционирования экосистемы. Первые концептуальные модели качественного уровня появились только вХХ столетии в работах В. Шелфорда (Shelford, I913), М. Хэвиленда (Haviland, 1926), В. Саммеохэйса и Ч. Элгoнa (Summerhayes, Elton, 1923, 1928) и некоторых других исследователей. Обеспечение же конгтептуальных моделей экосистем количественными данными о чмсленности и биомассе популяций, запасе оргагнического вещества и минеральных элементов, а тем более о динамике этих показателей для различных экосистем стало возможным только на основе исследований Международной биологической программы (1964-1974), в итоговых публпкациях которой представлены кснцептуальные модели важнейших типов зкосистем (Ресурсы биосферы, т. 1, 2, 1975; International Biological Programme. Publications, 1975-1979). В то же время наряду с такими общеизвестными достоинствами концептуальных моделей, как универсальность, гибкость, богатство средств выражения и др., благодаря которым этот метод применяется к самым разным системам, ему свойственны и недостатки, как, например, высокая неоднозначность интерпретации и известная статичность, затрудняющая описание динамических систем. При количественном изучении динамики экосистем гораздо более эффективны методы математического моделирования. Математической моделью системы-оригинала Ψ0 = Ψ0(V0, X0, ∑0, F0) называется ее модель Ψ = Ψ (V, X, ∑, F), у которой в качестве элементов множеств V и X выступают математические переменные (обычно, скалярные функции времени t) на рассматриваемом интервале: t0 ≤ t ≤ tN: υ1(t), …, υk(t), x1(t), …, xn(t). Структура
 σ1(υ1, …, υk, x1, …, xn) = 0 σ1(υ1, …, υk, x1, …, xn) = 0
σm(υ1, …, υk, x1, …, xn) = 0 σm+1(υ1, …, υk, x1, …, xn) ≤ 0 σr(υ1, …, υk, x1, …, xn) ≤ 0
связывающих между собой внешние и внутренние переменные модели. Функция x1(t), …, xn(t) на интервале t0 ≤ t ≤ tN: x1(t) = F1 (υ1, …, υk, x01, …, x0n, t), xn(t) = Fn (υ1, …, υk, x01, …, x0n, t), (IV.10) удовлетворяющие уравнениям и неравенствам (IV.9) и заданным начальным условиям x1(t0) = x01, …, xn(t0) = x0n. В качестве примера рассмотрим идеализированную систему, состоящую из одной популяции, которая существует в условиях изобилия корма и при отсутствии врагов и паразитов. Предположим, что в этих условиях прирост популяции пропорционален достигнутой численности, причем удельная скорость прироста r зависит от единственного внешнего фактора – температуры окружающей среды, которая на рассматриваемом промежутке времени t0 ≤ t ≤ tN считается известной. Чтобы построить математическую модель такой системы, рассмотрим множество V, состоящее из одного элемента – входной функции υ(t), задающей динамику температуры окружающей среды при t0 ≤ t ≤ tN, а также множество X, тоже состоящее из одного элемента, действительной переменной x(t), обозначающей численность популяции в момент времени t. Структуру модели Ʃ образуют три математических соотношения:
Первое выражает линейную зависимость скорости роста популяции от ее численности с меняющимся во времени коэффициентом удельного прироста r(t). Второе служит математическим выражением зависимости r от температуры окружающей среды υ (функция θ(υ) считается известной). Третье задает начальную численность популяции при t = t0. Для нахождения функции модели, т.е. разрешающего оператора F системы (IV.11), подставим в первое уравнение выражение r через υ с помощью функции θ(υ):
Разделяя переменные (см. Кудрявцев, Демидович, 1975, с. 449):
и интегрируя от x0 до x и от t0 до t соответственно, где x0 = x(t0) и x = x(t), получаем
После потенцирования получаем окончательный результат:
Таким образом, функционирование модели выражается оператором
В зависимости от свойств разрешающего оператора F математические модели динамических систем классифицируются по разным признакам. Так, если для оператора F найдено точное аналитическое выражение, позволяющее для любых входных функций и начальных условий непосредственно определять значение переменных состояния x1, …, xn в любой нужный момент t, то модель принято называть аналитической. Аналитические модели обладают многими благоприятными свойствами, облегчающими их исследование и применение. Однако в подавляющем большинстве случаев нахождение аналитического выражения для разрешающего оператора F оказывается затруднительным или в принципе невозможным. В то же время, если совокупность уравнений и неравенств (IV.9) непротиворечива и полна, то нередко удается найти алгоритм (процедуру) численного решения этих уравнений на ЭВМ, в результате чего получается реализация оператора F в виде машинной программы, с помощью которой по входным и начальным данным рассчитываются значения переменных состояний x1 (t), …, xn (t) на интервале t0 ≤ t ≤ tN. Такие модели называются численными, или, чаще, имитационными. В зависимости степени определенности предсказания траектории (x1 (t), …, xn (t)) оператором F модели делятся на детерминированные и стохастические (вероятностные). Если в детерминированной модели значения переменных состояния определяются однозначно (с точностью до ошибок вычисления) (рис. IV.7, Б), то стохастическая модель для каждой переменной xi дает распределение возможных значений, характеризуемое такими вероятностными показателями, как математическое ожидание M{xi }, среднее квадратическое отклонение σ{xi } и т.п. (рис. IV.7, Б).
Рис. (IV.7). Детерминированная (А) и стохастическая (Б) модели динамики переменной xi(t). Для любого момента времени t детерминированная модель предсказывает единственное значение переменной xi(t), а стохастическая модель показывает интервал По характеру временного описания динамики переменных состояния xi(t) различаются дискретные и непрерывные модели. Дискретная модель описывает поведение системы на фиксированной последовательности моментов времени t0 < t1 < … < tj < … < tN, тогда как в непрерывной модели значения переменных состояния могут быть рассчитаны для любой точки t рассматриваемого интервала [t0, tN]. Среди дискретных выделяются модели с фиксированным шагом по времени Δt = tj – tj-1, который не может быть изменен без глубокой перестройки всей модели. Например, в моделях динамики популяций организмов с непрерывающимися поколениями, сменяющимися только один раз в год, принимается Δt = 1 год (Варли, Градуэлл, Хасселл, 1978). В отличие от них существуют дискретные модели, в которых шаг по времени Δt может неограниченно уменьшаться (в пределах возможностей используемой ЭВМ), вследствие чего такие модели по детальности описания временных изменений приближаются к непрерывным. В частности, таковы модели, получающиеся в результате дискретизации непрерывного описания изучаемой системы в процессе приближенного численного решения дифференциальных уравнений. Следующий важный признак, по которому различаются математические модели экосистем, - это характер описания их пространственного строения. Модели, в которых пространственное строение экосистемы не рассматривается, т.е. в качестве переменных состояния фигурируют зависящие только от времени переменные xi(t), i = 1, …, n, принято называть моделями с сосредоточенными значениями (или точечными моделями), в отличие от моделей с распределенными значениями, в которых переменные состояния xi зависят не только от времени, но и от пространственных координат (одной или нескольких). Например, при моделировании водной экосистемы в качестве переменных состояния можно взять усредненные по площади и суммированные по глубине значения биомасс популяций, запасов биогенных элементов и т.д., выраженные, например, в граммах под площадью зеркала воды в 1 кв. м, - это будет модель с сосредоточенными значениями (Алексеев, 1975). Если в модели учитывается гетерогенность по глубине (координата z), т.е. xi = xi (z,t), то получается (очевидно, более детальная) модель с распределенными значениями по глубине, но все еще осредненными по плоскости (x,y). При описании мелкого, хорошо перемешиваемого по вертикали, но гетерогенного по плоскости водоема целесообразно в качестве переменных состояния использовать функции вида xi = xi (x,y,t). Наконец, вводя все три пространственные координаты xi = xi (x, y, z, t), получают модель с пространственно распределенными значениями.
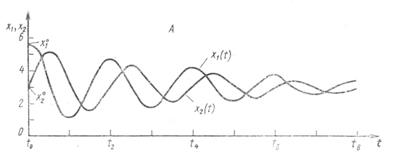
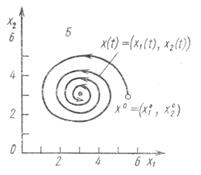
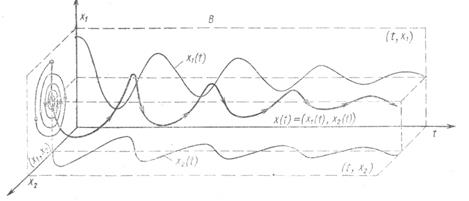
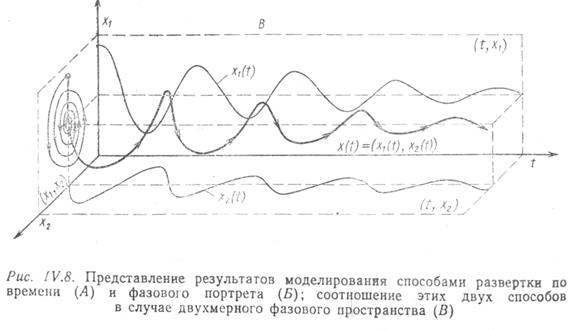
Рис. IV.8. Представление результатов моделирования способами развертки по времени (А) и фазового портрета (Б); соотношение этих двух способов в случае двухмерного фазового пространства (В)
Завершая краткое введение в метод моделирования, остановимся на некоторых способах визуального представления результатов моделирования. Наиболее часто используется так называемых способ развертки во времени, который состоит в построении таблиц или графиков изменения входных переменных и переменных состояния как функций времени t (рис. IV.8 (А)). При всех его достоинствах этот способ не всегда (особенно при большом числе переменных) дает наглядное представление взаимосвязей между переменными. Поэтому в дополнение к нему нередко используется так зазываемый способ фазовых портретов, когда на график наносится изображение траектории системы в пространстве состояний (при n = 2 или 3) или проекции этой траектории на координатные плоскости (xi, xj), образованные различными парами координат при n > 3 (рис. IV.8 (Б)). Время присутствует на фазовом портрете неявно, через указание тем или иным способом направления движения изображающей точки вдоль траектории (например, с помощью стрелок или отметок времени вдоль траектории). Соотношение способов развертки во времени и фазового портрета поясняет рис. IV.8 (В).
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 819; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.015 с.) |

 V0, X1
V0, X1 
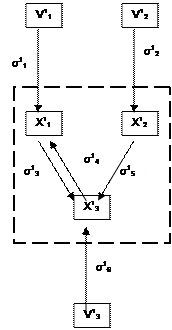

 Рис. IV.5. Переход от системы-оригинала Ψ0(V0, X0, ∑0, F0) к модели Ψ (V, X, ∑, F).
Рис. IV.5. Переход от системы-оригинала Ψ0(V0, X0, ∑0, F0) к модели Ψ (V, X, ∑, F).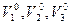 ; внутренний состав X0 - четырьмя элементами
; внутренний состав X0 - четырьмя элементами 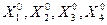 , а структура ∑0 представлена девятью связями
, а структура ∑0 представлена девятью связями 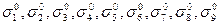 . Пусть, исходя из задачи исследования, оказалось возможным исключить из системы S° элемент
. Пусть, исходя из задачи исследования, оказалось возможным исключить из системы S° элемент 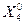 , а также связи
, а также связи 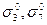 и
и 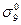 . Результатом такого огрубления явилась система Ψ1 = Ψ1(V1, X1, ∑1, F1),где
. Результатом такого огрубления явилась система Ψ1 = Ψ1(V1, X1, ∑1, F1),где 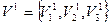 ;
; 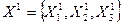 ;
; 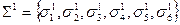 ;
;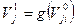 ;
; 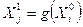 , i = 1, 2, 3;
, i = 1, 2, 3;  ;
; 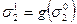 ;
; 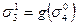 ;
; 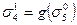 ;
; 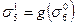 ;
; 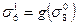 .
. и
и 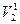 в один элемeнт V1, элементы
в один элемeнт V1, элементы 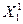 и
и 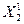 - в элемент X1,
- в элемент X1, 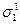 и
и 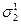 - в одну связь σ1 и связи
- в одну связь σ1 и связи 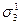 и
и 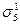 – в одну связь σ2, в результате чего получается система Ψ = Ψ (V, X, ∑, F), где X = {X1, X2}; V = {V1, V2}; ∑ = {σ1, σ2, σ3, σ4}; причем
– в одну связь σ2, в результате чего получается система Ψ = Ψ (V, X, ∑, F), где X = {X1, X2}; V = {V1, V2}; ∑ = {σ1, σ2, σ3, σ4}; причем 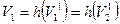 ;
; 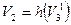 ;
; 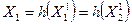 ;
; 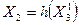 ;
; 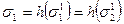 ;
; 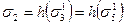 ;
; 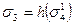 ;
; 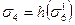 .
.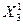 , связанные отношением
, связанные отношением 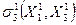 , мы видим, что их образы - элементы X1 и X2, связаны в модели отношением σ2, которое есть не что иное, как образ отношения
, мы видим, что их образы - элементы X1 и X2, связаны в модели отношением σ2, которое есть не что иное, как образ отношения 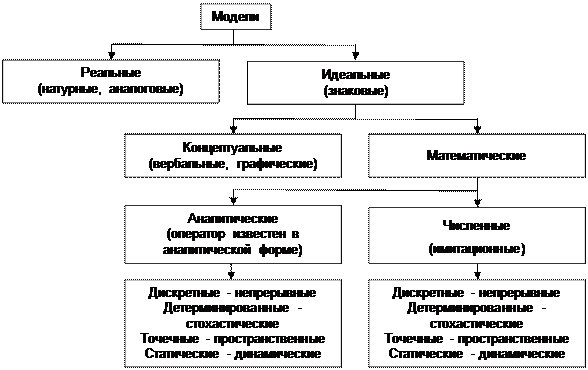
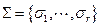 представляет собой множество математических соотношений между этими переменными, которые обычно формулируются в виде уравнений и неравенств вида
представляет собой множество математических соотношений между этими переменными, которые обычно формулируются в виде уравнений и неравенств вида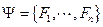 есть не что иное, как разрешающий оператор совокупности математических соотношений (IV.9), позволяющих по заданным входам υ1(t), …, υk(t); t0 ≤ t ≤ tN: υ1(t), с той или иной определенностью (от абсолютной детерминированности до размытого вероятностного описания) находить функции
есть не что иное, как разрешающий оператор совокупности математических соотношений (IV.9), позволяющих по заданным входам υ1(t), …, υk(t); t0 ≤ t ≤ tN: υ1(t), с той или иной определенностью (от абсолютной детерминированности до размытого вероятностного описания) находить функции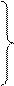
 (IV.11)
(IV.11)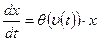 . (IV.12)
. (IV.12)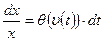 (IV.13)
(IV.13)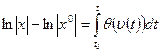 (IV.14)
(IV.14)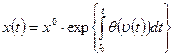 (IV.15)
(IV.15)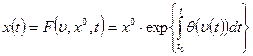 (IV.16)
(IV.16)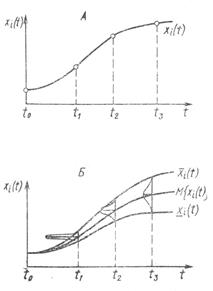
 , содержащий величину
, содержащий величину 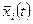 и ее распределение в этом интервале (в частности, математическое ожидание M{xi (t)}, среднее квадратическое отклонение σ{xi (t)} и другие статистические показатели).
и ее распределение в этом интервале (в частности, математическое ожидание M{xi (t)}, среднее квадратическое отклонение σ{xi (t)} и другие статистические показатели).