
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы решения систем нелинейных уравненийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте СОДЕРЖАНИЕ
Введение ……………………………………………………………......1 1. МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.. 2 2. ВЕКТОРНАЯ ЗАПИСЬ НЕЛИНЕЙНЫХ СИСТЕМ. 2 3. МЕТОД НЬЮТОНА, ЕГО РЕАЛИЗАЦИИ И МОДИФИКАЦИИ.. 4 3.1. МЕТОД НЬЮТОНА.. 4 3.2. МОДИФИЦИРОВАННЫЙ МЕТОД НЬЮТОНА …………………………………..6 3.3. МЕТОД НЬЮТОНА С ПОСЛЕДОВАТЕЛЬНОЙ АППРОКСИМАЦИЕЙ МАТРИЦ 7 3.4. РАЗНОСТНЫЙ МЕТОД НЬЮТОНА.. 9 3.5. ОБОБЩЕНИЕ ПОЛЮСНОГО МЕТОДА НЬЮТОНА НА МНОГОМЕРНЫЙ СЛУЧАЙ 9 4. ДРУГИЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.. 16 4.1. МЕТОД ПРОСТЕЙШИХ СЕКУЩИХ.. 16 4.2. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ.. 17 4.3. МЕТОД БРАУНА.. 19 4.4. МЕТОД СЕКУЩИХ БРОЙДЕНА.. 22 4.5. О РЕШЕНИИ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДАМИ СПУСКА.. 27 Практическая часть …………………………………………………………...33 Список источников ……………………………………………………………..44
Введение Вычислительная математика — раздел математики, включающий круг вопросов, связанных с производством вычислений и использованием компьютеров. В более узком понимании вычислительная математика — теория численных методов решения типовых математических задач.
К задачам вычислительной математики относят: -решение систем линейных уравнений -нахождение собственных значений и векторов матрицы -нахождение сингулярных значений и векторов матрицы -решение нелинейных алгебраических уравнений -решение систем нелинейных алгебраических уравнений -решение дифференциальных уравнений (как обыкновенных дифференциальных уравнений, так и уравнений с частными производными) -решение систем дифференциальных уравнений -решение интегральных уравнений -задачи аппроксимации -задачи интерполяции -задачи экстраполяции -задачи численной оптимизации
Основное отличие вычислительной математики заключается в том, что при решении вычислительных задач человек оперирует машинными числами, которые являются дискретной проекцией вещественных чисел на конкретную архитектуру компьютера. Так, например если взять машинное число длиной в 8 байт, то в нём можно запомнить только 264 разных чисел, поэтому важную роль в вычислительной математике играют оценки точности алгоритмов и их устойчивость к представлениям машинных чисел в компьютере. Именно поэтому, например, для решения линейной системы алгебраических уравнений очень редко используется вычисление обратной матрицы, так как этот метод может привести к ошибочному решению в случае с сингулярной матрицей, а очень распространённый в линейной алгебре метод, основанный на вычислении определителя матрицы и её дополнения требует гораздо больше арифметических операций, чем любой устойчивый метод решения линейной системы уравнений. МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ Рассматривается ряд методов решения систем алгебраических и трансцендентных уравнений. Среди них метод простых итераций, метод Ньютона в разных модификациях (в частности, n -полюсный метод Ньютона), метод Брауна, метод секущих Бройдена. Показывается связь между данной задачей и за дачей безусловной минимизации функции нескольких переменных. Проводится сравнение методов на примере решения конкретной системы. С единых позиций изучается сходимость основного и упрощенного методов Ньютона и метода, получаемого из метода Ньютона применением итерационного процесса Шульца для приближенного обращения матриц Якоби. МЕТОД НЬЮТОНА, ЕГО РЕАЛИЗАЦИИ И МОДИФИКАЦИИ
МЕТОД НЬЮТОНА Пусть (
имеет те же решения, что и исходное уравнение (2.1а), и для приближенного нахождения этих решений можно формально записать итерационный процесс
имеющий вид метода простых итераций (4.2.1b) при Положим
— матрица Якоби вектор-функции F(x). Подставив это
обобщающего на многомерный случай скалярный метод Ньютона (5.14). Эту формулу, требующую обращения матриц на каждой итерации, можно переписать в неявном виде:
Применение (3.1.3) предполагает при каждом k = 0,1,2,... решение линейной алгебраической системы
относительно векторной поправки
К решению таких линейных систем можно привлекать самые разные методы как прямые, так и итерационные в зависимости от размерности n решаемой задачи и специфики матриц Якоби Сравнивая (3.1.3) с формальным разложением F(x) в ряд Тейлора
видим, что последовательность (
линейным уравнением
т. е. с пошаговой линеаризацией. Как следствие этого факта, можно рассчитывать, что при достаточной гладкости F(x) и достаточно хорошем начальном приближении Новым, по сравнению со скалярным случаем, фактором, осложняющим применение метода Ньютона к решению n-мерных систем, является необходимость решения n-мерных линейных задач на каждой итерации (обращения матриц в (3.1.2) или решения СЛАУ в (3.1.3)), вычислительные затраты на которые растут с ростом n, вообще говоря, непропорционально быстро. Уменьшение таких затрат — одно из направлений модификации метода Ньютона.
РАЗНОСТНЫЙ МЕТОД НЬЮТОНА На базе метода Ньютона (3.1.2) можно построить близкий к нему по поведению итерационный процесс, не требующий вычисления производных. Сделаем это, заменив частные производные в матрице Якоби J(x) разностными отношениями, т.е. подставив в формулу (3.1.1) вместо
При удачном задании последовательности малых векторов
МЕТОД ПРОСТЕЙШИХ СЕКУЩИХ Можно связать задание последовательности (
где
k =1,2,3,…. Этот метод является. двухшаговым и требует задания двух начальных точек К методу секущих так же, как и к методу Ньютона, можно применить пошаговую аппроксимацию обратных матриц на основе метода Шульца. Расчетные формулы этой модификации легко выписать, заменив в совокупности формул ААМН (3.3.1) матрицу МЕТОД ПРОСТЫХ ИТЕРАЦИЙ
Пусть система (2.1) имеет вид (преобразована к виду):
или иначе, в компактной записи,
где
Для этой задачи о неподвижной точке нелинейного отображения
которое определяет метод простых итераций (МПИ) (или метод последовательных приближений) для задачи (4.2.1). Если начать процесс построения последовательности ( Теорема 4.1. Пусть функция Ф(х) и замкнутое множество 1) 2) Тогда Ф(х) имеет в М единственную неподвижную точку
Теорема 4.2. Пусть функция Ф(х) дифференцируема в замкнутом шаре
Если потребовать непрерывную дифференцируемость Ф(х), то более просто перейти от теоремы 4.1 к теореме 4.2, применив следующее утверждение. Лемма 4.1. Пусть функция
Запись МПИ (4.2.1b) в развернутом виде, т.е. совокупность рекуррентных равенств
напоминает МПИ для СЛАУ, который укладывается в эту схему, если все функции
Заметим, что как и для линейных систем, отдельные уравнения в методе (4.2.2) неравноправны, т.е. перемена местами уравнений системы (4.2.1) может изменить в каких-то пределах число итераций и вообще ситуацию со сходимостью последовательности итераций. Чтобы применить метод простых итерации или его зейделеву модификацию (4.2.2) к исходной системе (2.1), нужно, как и в скалярном случае, сначала тем или иным способом привести ее к виду (4.2.1). Это можно сделать, например, умножив (2.1а) на некоторую неособенную n-x-n матрицу – А и прибавив к обеим частям уравнения - A F (x)=0 вектор неизвестных х. Полученная система x = x-A F (x) эквивалентна данной и имеет вид задачи о неподвижной точке (4.2.1а). проблема теперь состоит лишь в подборе матричного параметра А такого, при котором вектор-функция Ф(х):=х-А F (x) обладала бы нужными свойствами.
МЕТОД БРАУНА В отличие от пошаговой линеаризации векторной функции F(x), приведшей к методу Ньютона (3.1.2), Брауном (1966 г.) предложено проводить на каждом итерационном шаге поочередную линеаризацию компонент вектор-функции F(x), т.е. линеаризовать в системе (2.1) сначала функцию Пусть требуется найти решение системы
и пусть уже получены приближения Подменим первое уравнение системы (4.3.1) линейным, полученным по формуле Тейлора для функции двух переменных:
Отсюда выражаем х (обозначим этот результат через
При
которое будем считать лишь промежуточным приближением (т.е. не Подставив в g(x, у) вместо х переменную
При нахождении производной G'(y) нужно учесть, что G(y) = g( Дифференцируя по у равенство (4.3.2), получаем выражение
подстановка которого в предыдущее равенство при
При известных значениях G(
Заменяя в (4.3.2) переменную у найденным значением
Таким образом, реализация метода Брауна решения двумерных нелинейных систем вида (4.3.1) сводится к следующему. При выбранных начальных значениях каждое
счет по которым должен выполнятся в той очередности, в которой они записаны. Вычисления в методе Брауна естественно заканчивать, когда выполнится неравенство Указывая на наличие квадратичной сходимости метода Брауна, отмечают, что рассчитывать на его большую по сравнению с методом Ньютона эффективность в смысле вычислительных затрат можно лишь в случае, когда фигурирующие в нем частные производные заменяются разностными отношениями. МЕТОД СЕКУЩИХ БРОЙДЕНА Чтобы приблизиться к пониманию идей, лежащих в основе предлагаемого вниманию метода, вернемся сначала к изучавшемуся в двух предыдущих главах одномерному случаю. В процессе построения методов Ньютона и секущих решения нелинейного скалярного уравнения
Приравнивание к нулю последней, т.е. решение линейного уравнения
порождает итерационную формулу
для вычисления приближений к корню уравнения (4.4.1). Если потребовать, чтобы заменяющая функцию f(x) вблизи точки
подстановка которого в (4.4.2) приводит к известному методу Ньютона (5.14). Если же исходить из того, что наряду с равенством
или, в соответствии с (4.4.1а)
то получаем коэффициент
превращающий (4.4.2) в известную формулу секущих. Равенство (4.4.3), переписанное в виде
называют соотношением секущих в В n-мерном векторном пространстве
где
соотношение секущих в
Аналогично одномерному случаю, а именно, по аналогии с формулой (4.4.2), будем искать приближения к решению
Желая, чтобы эта формула обобщала метод секущих (5.32), обратимую n x n-матрицу При формировании матрицы Переходя от имеющейся в точке
к такой же модели в точке
мы не имеем о матрице линейного преобразования
Представим вектор
Подстановкой этого представления вектора
Анализируя выражение (4.4.9), замечаем, что первое слагаемое в нем не может быть изменено, поскольку
- фиксированный вектор при фиксированном k. Поэтому минимальному изменению аффинной модели
Непосредственной проверкой убеждаемся, что условие (4.4.10) будет выполнено, если матричную поправку
Таким образом, приходим к так называемой формуле пересчета С. Бройдена (1965 г.)
которая позволяет простыми вычислениями перейти от старой матрицы Совокупность формул (4.4.6), (4.4.11) вместе с обозначениями (4.4.5) называют методом секущих Бройдена или просто методом Бройдена решения систем нелинейных числовых уравнений. Хотя в методах секущих обычным является задание двух начальных векторов ( 1. решить линейную систему
относительно вектора 2. найти векторы
3. сделать проверку на останов(например, с помощью проверки на малость величин
В качестве матрицы при достаточной близости Как и в случаях применения других методов решения нелинейных систем, проверка выполнимости каких-то условий сходимости итерационного процесса Бройдена весьма затруднительна. Формуле пересчета (4.4.14) в итерационном процессе можно придать чуть более простой вид. Так как, в силу (4.4.12) и (4.4.13),
а
то из формулы (4.4.14) получаем формально эквивалентную ей формулу пересчета
которую можно использовать вместо (4.4.14) в совокупности с формулой (4.4.6) или с (4.4.12), (4.4.13) (без вычисления вектора
Практическая часть Вычисление погрешностей Задание Пусть a, b, y – приближенные числа с верными в строгом смысле значащими цифрами, х – верное число. Вычислите:
Оцените погрешность результата. Результаты расчетов расположите в таблице. Решение Представлено на рисунке 1.1.
Рисунок 1.1 – Результаты расчетов.
СОДЕРЖАНИЕ
Введение ……………………………………………………………......1 1. МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.. 2 2. ВЕКТОРНАЯ ЗАПИСЬ НЕЛИНЕЙНЫХ СИСТЕМ. 2 3. МЕТОД НЬЮТОНА, ЕГО РЕАЛИЗАЦИИ И МОДИФИКАЦИИ.. 4 3.1. МЕТОД НЬЮТОНА.. 4 3.2. МОДИФИЦИРОВАННЫЙ МЕТОД НЬЮТОНА …………………………………..6 3.3. МЕТОД НЬЮТОНА С ПОСЛЕДОВАТЕЛЬНОЙ АППРОКСИМАЦИЕЙ МАТРИЦ 7 3.4. РАЗНОСТНЫЙ МЕТОД НЬЮТОНА.. 9 3.5. ОБОБЩЕНИЕ ПОЛЮСНОГО МЕТОДА НЬЮТОНА НА МНОГОМЕРНЫЙ СЛУЧАЙ 9 4. ДРУГИЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.. 16 4.1. МЕТОД ПРОСТЕЙШИХ СЕКУЩИХ.. 16 4.2. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ.. 17 4.3. МЕТОД БРАУНА.. 19 4.4. МЕТОД СЕКУЩИХ БРОЙДЕНА.. 22 4.5. О РЕШЕНИИ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДАМИ СПУСКА.. 27 Практическая часть …………………………………………………………...33 Список источников ……………………………………………………………..44
Введение Вычислительная математика — раздел математики, включающий круг вопросов, связанных с производством вычислений и использованием компьютеров. В более узком понимании вычислительная математика — теория численных методов решения типовых математических задач.
К задачам вычислительной математики относят: -решение систем линейных уравнений -нахождение собственных значений и векторов матрицы -нахождение сингулярных значений и векторов матрицы -решение нелинейных алгебраических уравнений -решение систем нелинейных алгебраических уравнений -решение дифференциальных уравнений (как обыкновенных дифференциальных уравнений, так и уравнений с частными производными) -решение систем дифференциальных уравнений -решение интегральных уравнений -задачи аппроксимации -задачи интерполяции -задачи экстраполяции -задачи численной оптимизации
Основное отличие вычислительной математики заключается в том, что при решении вычислительных задач человек оперирует машинными числами, которые являются дискретной проекцией вещественных чисел на конкретную архитектуру компьютера. Так, например если взять машинное число длиной в 8 байт, то в нём можно запомнить только 264 разных чисел, поэтому важную роль в вычислительной математике играют оценки точности алгоритмов и их устойчивость к представлениям машинных чисел в компьютере. Именно поэтому, например, для решения линейной системы алгебраических уравнений очень редко используется вычисление обратной матрицы, так как этот метод может привести к ошибочному решению в случае с сингулярной матрицей, а очень распространённый в линейной алгебре метод, основанный на вычислении определителя матрицы и её дополнения требует гораздо больше арифметических операций, чем любой устойчивый метод решения линейной системы уравнений. МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ Рассматривается ряд методов решения систем алгебраических и трансцендентных уравнений. Среди них метод простых итераций, метод Ньютона в разных модификациях (в частности, n -полюсный метод Ньютона), метод Брауна, метод секущих Бройдена. Показывается связь между данной задачей и за дачей безусловной минимизации функции нескольких переменных. Проводится сравнение методов на примере решения конкретной системы. С единых позиций изучается сходимость основного и упрощенного методов Ньютона и метода, получаемого из метода Ньютона применением итерационного процесса Шульца для приближенного обращения матриц Якоби.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1916; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.10 (0.012 с.) |

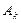 ) — некоторая последовательность невырожденных вещественных n x n-матриц. Тогда, очевидно, последовательность задач
) — некоторая последовательность невырожденных вещественных n x n-матриц. Тогда, очевидно, последовательность задач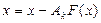 , k = 0,1,2,...
, k = 0,1,2,...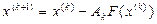 , k = 0,1,2,... (3.1.1)
, k = 0,1,2,... (3.1.1) . В случае
. В случае  - это действительно МПИ с линейной сходимостью последовательности (
- это действительно МПИ с линейной сходимостью последовательности ( ) Если же
) Если же  , где
, где

 , (3.1.2)
, (3.1.2) . (3.1.3)
. (3.1.3)
 , а затем прибавление этой поправки к текущему приближению для получения следующего:
, а затем прибавление этой поправки к текущему приближению для получения следующего: .
. (например, можно учитывать их симметричность, разреженность и т.п.).
(например, можно учитывать их симметричность, разреженность и т.п.). ,
, ) в методе Ньютона получается в результате подмены при каждом k=0,1,2,... нелинейного уравнения F(x) = 0 или, что то же (при достаточной гладкости F(x)), уравнения
) в методе Ньютона получается в результате подмены при каждом k=0,1,2,... нелинейного уравнения F(x) = 0 или, что то же (при достаточной гладкости F(x)), уравнения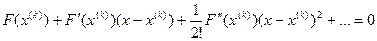

 сходимость порождаемой методом Ньютона последовательности (
сходимость порождаемой методом Ньютона последовательности ( будет квадратичной и в многомерном случае. Имеется ряд теорем, устанавливающих это при тех или иных предположениях. В частности, одна из таких теорем приводится ниже.
будет квадратичной и в многомерном случае. Имеется ряд теорем, устанавливающих это при тех или иных предположениях. В частности, одна из таких теорем приводится ниже. где
где
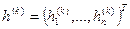 (постоянной или сходящейся к нулю) полученный таким путем разностный (или иначе, дискретный) метод Ньютона имеет сверхлинейную, вплоть до квадратичной, скорость сходимости и обобщает на многомерный случай метод (5.29). При задании векторного параметра h — шага дискретизации — следует учитывать точность машинных вычислений (macheps), точность вычисления значений функций
(постоянной или сходящейся к нулю) полученный таким путем разностный (или иначе, дискретный) метод Ньютона имеет сверхлинейную, вплоть до квадратичной, скорость сходимости и обобщает на многомерный случай метод (5.29). При задании векторного параметра h — шага дискретизации — следует учитывать точность машинных вычислений (macheps), точность вычисления значений функций  , средние значения получаемых приближений.
, средние значения получаемых приближений. ) с какой-либо сходящейся к нулю векторной последовательностью, например, с последовательность невязок (
) с какой-либо сходящейся к нулю векторной последовательностью, например, с последовательность невязок ( ) или поправок (
) или поправок ( ). Так, полагая
). Так, полагая  где j=1,…n, a k=1,2, …,приходим к простейшему методу секущих — обобщению скалярного метода секущих (5.32):
где j=1,…n, a k=1,2, …,приходим к простейшему методу секущих — обобщению скалярного метода секущих (5.32): , (4.1.1)
, (4.1.1)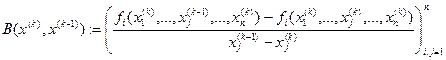
 и
и  . При п = 1 сходимость метода(4.1.1) имеет порядок
. При п = 1 сходимость метода(4.1.1) имеет порядок  . Можно рассчитывать на такую же скорость и в многомерном случае.
. Можно рассчитывать на такую же скорость и в многомерном случае. на матрицу
на матрицу  из (4.1.1)
из (4.1.1)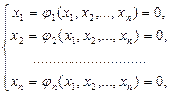 (4.2.1)
(4.2.1) , (4.2.1а)
, (4.2.1а) .
. запишем формально рекуррентное равенство,
запишем формально рекуррентное равенство, (4.2.1b)
(4.2.1b) и продолжить по формуле (4.2.1b), то при определенных условиях эта последовательность со скоростью геометрической прогрессии будет приближаться к вектору
и продолжить по формуле (4.2.1b), то при определенных условиях эта последовательность со скоростью геометрической прогрессии будет приближаться к вектору  — неподвижной точке отображения Ф(х). А именно, справедлива следующая теорема.
— неподвижной точке отображения Ф(х). А именно, справедлива следующая теорема. таковы, что:
таковы, что:
 ;
;

 сходится к
сходится к 

 причем
причем  :
: . Тогда, если центр
. Тогда, если центр 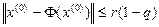 , то справедливo заключение теоремы 4.1 с М=S.
, то справедливo заключение теоремы 4.1 с М=S. и пусть
и пусть 
 .
.
 — линейные. Учитывая, что в линейном случае, как правило, по сравнению с МПИ более эффективен метод Зейделя, здесь тоже может оказаться полезной модификация. А именно, вместо (4.2.1b) можно реализовать следующий метод итераций:
— линейные. Учитывая, что в линейном случае, как правило, по сравнению с МПИ более эффективен метод Зейделя, здесь тоже может оказаться полезной модификация. А именно, вместо (4.2.1b) можно реализовать следующий метод итераций: (4.2.2)
(4.2.2) , затем
, затем  и т.д., и последовательно решать получаемые таким образом уравнения. Чтобы не затенять эту идею громоздкими выкладками и лишними индексами, рассмотрим вывод расчетных формул метода Брауна в двумерном случае.
и т.д., и последовательно решать получаемые таким образом уравнения. Чтобы не затенять эту идею громоздкими выкладками и лишними индексами, рассмотрим вывод расчетных формул метода Брауна в двумерном случае. (4.3.1)
(4.3.1) .
.
 ):
): (4.3.2)
(4.3.2)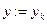 находим значение
находим значение  переменной
переменной 
 ), поскольку оно не учитывает второго уравнения системы (4.3.1).
), поскольку оно не учитывает второго уравнения системы (4.3.1). , придем к некоторой функции G(y):= g(
, придем к некоторой функции G(y):= g( (4.3.3)
(4.3.3)
 дает
дает
 ) = g(
) = g( ):
):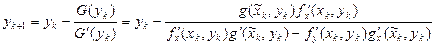


 последующее приближение по методу Брауна находится при k = 0,1,2,... с помощью совокупности формул
последующее приближение по методу Брауна находится при k = 0,1,2,... с помощью совокупности формул
 ,
,


 (с результатом
(с результатом  ). В ходе вычислений следует контролировать немалость знаменателей расчетных формул. Заметим, что функции f и g в этом методе неравноправны, и перемена их ролями может изменить, ситуацию со сходимостью.
). В ходе вычислений следует контролировать немалость знаменателей расчетных формул. Заметим, что функции f и g в этом методе неравноправны, и перемена их ролями может изменить, ситуацию со сходимостью. (4.4.1)
(4.4.1) подменяется линейной функцией (аффинной моделью)
подменяется линейной функцией (аффинной моделью)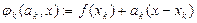 (4.4.1а)
(4.4.1а) ,
, (4.4.2)
(4.4.2) имела в этой точке одинаковую с ней производную, то, дифференцируя (4.4.1а), получаем Значение коэффициента
имела в этой точке одинаковую с ней производную, то, дифференцируя (4.4.1а), получаем Значение коэффициента ,
, должно иметь место совпадение функций f(x) и
должно иметь место совпадение функций f(x) и  т.е. из равенства
т.е. из равенства ,
, , (4.4.3)
, (4.4.3) ,
, ,
, Оно легко обобщается на n -мерный случай и лежит в основе вывода метода Бройдена. Опишем этот вывод.
Оно легко обобщается на n -мерный случай и лежит в основе вывода метода Бройдена. Опишем этот вывод. соотношение секущих представляется равенством
соотношение секущих представляется равенством , (4.4.4)
, (4.4.4) — известные n-мерные векторы,
— известные n-мерные векторы,  — данное нелинейное отображение, а
— данное нелинейное отображение, а  — некоторая матрица линейного преобразования в
— некоторая матрица линейного преобразования в  ,
,  (4.4.5)
(4.4.5) (4.4.4а)
(4.4.4а) (4.4.6)
(4.4.6) в другой заданный вектор
в другой заданный вектор  (отсюда — ясность в понимании того, что могут быть различные обобщения одномерного метода секущих).
(отсюда — ясность в понимании того, что могут быть различные обобщения одномерного метода секущих). будем рассуждать следующим образом.
будем рассуждать следующим образом. аффинной модели функции F(x)
аффинной модели функции F(x) (4.4.7)
(4.4.7)
 (4.4.8)
(4.4.8) . Вычтем из равенства (4.4.8) определяющее
. Вычтем из равенства (4.4.8) определяющее  равенство (4.4.7) и преобразуем результат, привлекая соотношение секущих (4.4.4). Имеем:
равенство (4.4.7) и преобразуем результат, привлекая соотношение секущих (4.4.4). Имеем:
 в виде линейной комбинации фиксированного вектора
в виде линейной комбинации фиксированного вектора  ,
, 
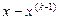 в разность
в разность  (4.4.9)
(4.4.9)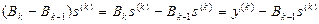
 будет отвечать случай, когда второе слагаемое в (4.4.9) будет нуль-вектором при Iвсяких векторах t, ортогональных векторам
будет отвечать случай, когда второе слагаемое в (4.4.9) будет нуль-вектором при Iвсяких векторах t, ортогональных векторам  следует находить из условия
следует находить из условия
 . (4.4.10)
. (4.4.10) взять в виде одноранговой nхn-матрицы
взять в виде одноранговой nхn-матрицы .
. (4.4.11)
(4.4.11) к новой
к новой  ), для метода Бройдена характерно другое начало итерационного процесса. Здесь нужно задать один начальный вектор
), для метода Бройдена характерно другое начало итерационного процесса. Здесь нужно задать один начальный вектор  и далее в цикле по k = 0,1,2,... последовательно выполнять следующие операции:
и далее в цикле по k = 0,1,2,... последовательно выполнять следующие операции: (4.4.12)
(4.4.12)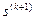 :
: и
и  :
: ,
,  ; (4.4.13)
; (4.4.13) и/или
и/или  и если нужная точность не достигнута, вычислить новую матрицу
и если нужная точность не достигнута, вычислить новую матрицу  (4.4.14)
(4.4.14) или какую-нибудь ее аппроксимацию. При этом получаемые далее пересчетом (4.4.14) матрицы
или какую-нибудь ее аппроксимацию. При этом получаемые далее пересчетом (4.4.14) матрицы  ,
,  ,... не всегда можно считать близкими к соответствующим матрицам Якоби
,... не всегда можно считать близкими к соответствующим матрицам Якоби  ,
,  ,... (что может иногда сыграть полезную роль при вырождении матриц
,... (что может иногда сыграть полезную роль при вырождении матриц  ). Но, в то же время, показывается, что при определенных требованиях к матрицам Якоби
). Но, в то же время, показывается, что при определенных требованиях к матрицам Якоби  матрицы
матрицы  с увеличением номера итерации k, то достаточно медленно. С помощью этого свойства доказываются утверждения о линейной сходимости(
с увеличением номера итерации k, то достаточно медленно. С помощью этого свойства доказываются утверждения о линейной сходимости( ,
, ,
, , (4.4.14а)
, (4.4.14а)



