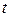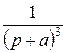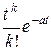Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коррекция линейных систем автоматического регулированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: исследовать влияние корректирующих устройств переходные процессы в линейных системах. Общие положения
В случае неустойчивости или неудовлетворительного качества переходных процессов в устойчивой системе в нее вводят корректирующие устройства (КУ). Они могут вводиться в прямую цепь – последовательные КУ, параллельно какому-либо элементу – параллельное КУ, в местную обратную связь – КУ обратной связи (ОС). Использование КУ ОС делает систему многоконтурной, они предпочтительнее других КУ. При коррекции ОС возможна линеаризация нелинейностей, устранение влияния нестабильности параметров звеньев, повышение устойчивости и качества систем. Местной ОС обычно охватывают усилители с большим коэффициентом усиления, элементы с нестабильными характеристиками, неустойчивые звенья. Корректирующие ОС могут быть жесткие и гибкие, структура и параметры ОС выбираются по требованиям к переходному процессу в системе и условиям устойчивости корректирующего контура. Корректирующие средства. Под улучшением качества процесса управления, помимо повышения точности в типовых режимах, понимается изменение динамических свойств системы с целью получения необходимого запаса устойчивости и быстродействия. В этой проблеме основное значение имеет обеспечение запаса устойчивости, т.к. стремление снизить ошибки системы приводит, как правило, к необходимости использовать такие значения коэффициента усиления, при которых без принятия специальных мер система оказывается неустойчивой. При решении задач повышения запасов устойчивости необходимо попытаться рациональным образом изменить ее параметры (коэффициенты передачи отдельных звеньев, постоянные времени и т.п.) так, чтобы удовлетворить требованиям качества. Если это невозможно в систему вводят корректирующие устройства (их иногда называют демпфирующими или стабилизирующими звеньями). Использование того или иного типа КУ определяется удобством технической реализации. КУ последовательного типа особенно удобны в тех случаях, когда в системе используются электрический сигнал в виде напряжения постоянного тока, величина которого линейно связана с сигналом ошибки КУ параллельного типа удобно применять в тех случаях, когда необходимо осуществить сложный закон управления с введение интегралов и производных от сигнала ошибки. КУ обратной связи находят более широкое применение вследствие простоты технической реализации. Это объясняется тем, что на вход КУ обратной связи поступает сигнал довольно высокого уровня, часто непосредственно с выхода системы, с входа усилителя мощности или с выхода исполнительного устройства. Отрицательные обратные связи имеют свойства уменьшать влияние нелинейностей тех участков цепи управления, которые ими охватываются. Так как практически все системы управления содержат те или иные нелинейности (люфт, зона нечувствительности и т.п.), ухудшающие качество работы системы, то использование КУ в виде отрицательных местных обратных связей, как правило, дает возможность добиться лучших результатов по сравнению с другими типами КУ. Можно перейти от КУ одного типа к КУ другого типа, формулы перехода получают приравниванием результирующих передаточных функций (передаточных функций скорректированной системы При последовательном КУ передаточная функция При параллельной коррекции:
При КУ обратной связи
Рисунок 6.1 – Коррекция обратной связью
где
Приравнивая все эти выражения можно получить шесть формул перехода от КУ одного типа к КУ другого типа, например:
Последовательные КУ. Наиболее просто последовательные КУ реализуются на пассивных RC, RL четырехполюсниках и имеют широкое распространение. Они могут быть представлены в виде обобщенной схемы:
 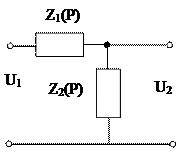
где
Параллельные корректирующие звенья. Параллельные КУ удобно применять при использовании сложных законов управления, когда необходимо вводить производные и интегралы от сигнала ошибки. Введение интеграла позволяет сделать систему астатической и следовательно снизить ошибки, лучше формировать изодромные звенья. Введение производных преследует обычно цель обеспечения устойчивости и запасов устойчивости. Введение интеграла
Рисунок 6.2 – Параллельная коррекция введением интеграла
где
Введение производных
Рисунок 6.3 – Параллельная коррекция введением производных
Обратные связи. Местные ОС могут быть положительными и отрицательными, жесткими и гибкими. Гибкие обратные связи изменяют динамику и работают в переходных режимах, а в установившемся состоянии она как бы отключаются. Жесткая ОС действует как в переходном так и установившемся состоянии. ОС является гибкой, если Введение жестких отрицательных ОС приводит к уменьшению коэффициента передачи и постоянных времени.
Рисунок 6.4 – Коррекция жесткой ОС
Отрицательные корректирующие ОС часто используют для охвата исполнительных двигателей и серводвигателей (вспомогательных двигателей), исполнительных механизмов. Это позволяет снизить влияние нелинейностей и нечувствительности на работу системы. Положительные корректирующие ОС находят значительно меньшее применение. Их можно использовать в качестве так называемых корректоров ошибки. Например:
Рисунок 6.5 – Коррекция положительной ОС
получается изодромное звено с
Методы повышения запаса устойчивости. Повышение запаса устойчивости, или демпфирование, системы сводится, в конечном счете, к рациональному перераспределению полюсов и нулей передаточной функции системы в разомкнутом состоянии. Наиболее наглядно это можно показать на АФЧХ разомкнутой системы, которую нужно с помощью КУ деформировать так, чтобы получить заданные запасы устойчивости. Наиболее просто использовать показатель колебательности М, тогда АФЧХ не должна заходить в окружность соответствующую заданному М.
Рисунок 6.5 – Коррекция положительной ОС
Деформация АФЧХ может быть произведена тремя основными способами: а) демпфирование с подавлением высоких частот; б) демпфирование с поднятием высоких частот; в) демпфирование с подавлением средних частот.
Демпфирование с подавлением высоких частот может осуществляться различными способами. Наиболее просто – введением последовательного КУ в виде апериодического звена с коэффициентом передачи K=1 и с большой постоянной времени.
Введение звена с большой постоянной времени делает все остальные постоянные времени относительно малыми, в результате чего достигается эффект демпфирования. Недостатком демпфирования с подавлением высоких частот является то, что снижение полосы пропускания системы означает понижение быстродействия. Поэтому этот способ используется только тогда, когда допустимо снижение быстродействия. Демпфирование с поднятием высоких частот. Положительный фазовый сдвиг (фазовое упреждение) может быть получен посредством включения в канал регулирования звеньев дифференцирующего типа. Если параллельной части основного канала включить идеально дифференцирующее звено, то будет получен дополнительный положительный фазовый сдвиг.
Рисунок 6.7 – Параллельная коррекция
Одновременно с положительным фазовым сдвигом звено увеличивает пропускание высоких частот. Могут применяться и два дифференцирующих звена, включенных последовательно, что соответствует введению первой и второй производной от сигнала ошибки. Могут использоваться и пассивные дифференцирующие звенья Демпфирование посредством поднятия высоких частот является универсальным методом, т.к. позволяет получить требуемый результат практически при любых передаточных функциях исходной системы, в том числе и при наличии неминимально-фазовых звеньев. Поднятие верхних частот расширяет полосу пропускания системы, что приводит к увеличению быстродействия и одновременно усиливает влияние на систему высокочастотных помех. При большом уровне помех может привести к неприемлемым результатам. Демпфирование с подавлением средних частот может быть осуществлено включением в цепь управления последовательного интегро-дифференцирующего звена с передаточной функцией:
Его ЛАЧХ и ФЧХ:

  
 


Звено подавляет усиление в некоторой области частот Вместо пассивного интегро-дифференцирующего звена можно применять его эквивалент – например гибкую обратную отрицательную связь к инерционному усилителю. По своим свойствам демпфирование с подавлением «средних» частот занимает промежуточное положение между двумя первыми методами. Таким образом, для получения заданного качества переходного процесса и точности в установившихся режимах в систему вводят КУ. Какова должна быть структура и параметры КУ для конкретной системы определяется в процессе синтеза системы. Под синтезом системы понимается направленный расчет, имеющий конечной целью отыскание рациональной структуры системы и определение оптимальных величин параметров ее звеньев. Синтез системы можно трактовать как инженерную задачу, сводящуюся к такому построению системы, при котором обеспечивается выполнение технических требований к ней; или как более узкую задачу – определение структуры и параметров КУ которые необходимо добавить к некоторой неизменной части системы, чтобы обеспечить требуемое качество (проектирование САУ). В более широком смысле синтез можно трактовать как вариационную задачу, рассматривая построение САУ при котором для данных условий работы (управляющие и возмущающие воздействия, помехи, ограничения по координатам, управлению и по времени) обеспечиваются теоретический минимум ошибки.
Порядок выполнения лабораторной работы
Рисунок 6.1 – Структурная схема системы
Для схемы на рисунке 6.1 выполнить: 1. Дать характеристику системы без 2. Записать передаточные функции 3. Записать передаточные функции 4. Собрать схему (рисунок 6.1) в программе VisSim, задавшись параметрами звеньев. Исследовать переходной процесс при ступенчатом входном сигнале при 5. Ввести жесткую ОС к 3-му звену. Записать 6. При выбранных ранее параметрах исследовать переходной процесс при ступенчатом входном сигнале и
Рисунок 6.2 – Структурная схема системы
Для схемы на рисунке 6.2 выполнить: 1. Дать характеристику системы без 2. Записать передаточные функции 3. Записать передаточные функции
4. Если жесткая ОС не делает систему устойчивой, значит надо вводить гибкую ОС. Структуру ОС можно выбрать из условия устойчивости замкнутого контура при отрицательной ОС. В качестве КУ используем реально дифференцирующее звено 5. Записать передаточные функции 6. Собрать схему (рисунок 6.2) в программе VisSim и проверить расчеты при ступенчатом входном сигнале на входе, изменяя
Содержание отчёта
1. Схемы исследования и результаты исследования. 2. Передаточные функции, характеристическое уравнение, условие устойчивости, характеристики систем. 3. Результаты расчетов.
Контрольные вопросы
1. Какие существуют способы коррекции линейных систем? 2. Какие звенья необходимо охватывать корректирующими обратными связями? 3. Как рассчитать параметры корректирующих обратных связей?
Лабораторная работа № 7 Изучение методов теории инвариантности для повышения точности систем Цель работы: изучить методы теории инвариантности для повышения точности систем.
Общие положения
Одним из наиболее эффективных способов повышения точности следящих систем является применение методов теории инвариантности. В общем случае инвариантность системы по какому-либо воздействию – это независимость выходной переменной системы от этого воздействия. Применение методов теории инвариантности наиболее эффективно в тех случаях, когда к следящим системам предъявляются высокие требования в отношении динамической точности. Основным методом, используемым при построении инвариантных систем, является введения второго канала передачи воздействия, по которому требуется обеспечить инвариантность. Следящие системы, в которых вводится второй канал передачи задающего воздействия также называют системами с комбинированным управлением, потому что в таких системах управление осуществляется как сигналом ошибки, так и сигналом задающего воздействия. При необходимости получения абсолютной (полной) инвариантности системы по какому-либо воздействию передаточные функции устройств, которые необходимо вводить во второй канал передачи, определяются из условия равенства нулю ошибки по этому воздействию. Однако при этом часто получаются передаточные функции компенсирующей цепи, содержащие производные высоких порядков. Поскольку реализовать такие передаточные функции практически не удается, поэтому чаще всего ограничиваются выполнением условий частичной инвариантности, т.е. обеспечивают инвариантность системы к определенным составляющим воздействий. На практике обычно ограничиваются введением в компенсирующую цепь производных не выше второго или третьего порядка. В большинстве случаев этого бывает достаточно для обеспечения высокой точности системы.
Рассмотрим пример систем с комбинированным управлением. Структурные схемы следящих систем с таким управлением приведены на рисунке 7.1.
Рисунок 7.1 – Структурные схемы систем с комбинированным управлением
Теоретически может быть рассчитана такая передаточная функция компенсирующей цепи В следящей системе с комбинированным управлением по входному сигналу (рисунок 7.1, а) передаточная функция компенсирующей цепи
Передаточная функция замкнутой системы
Условие (1) является условием абсолютной (полной) инвариантности следящей системы по входному сигналу. В следящей системе с комбинированным управлением по возмущению (рисунок 7.1, б) условием полной инвариантности является равенство В схеме, приведенной на рисунке 7.1, б, при выполнении условия Особенностью следящих систем с комбинированным управлением является то, что компенсирующие цепи при выполнении условий (1) и (2) не изменяют характеристическое уравнение замкнутой системы, а следовательно, не влияют на устойчивость. Реализация принципа комбинированного управления позволяет компенсировать ошибки, обусловленные действием входного сигнала и возмущения, но не устраняет переходную составляющую ошибки, обусловленную ненулевыми начальными условиями. Условия абсолютной инвариантности (1) и (2) получить на практике в большинстве случаев не удается из-за физической нереализуемости требуемых передаточных функций компенсирующих цепей, представляющих собой дроби, у которых порядок числителя больше порядка знаменателя. Приближенная реализация условий (1) и (2) позволяет получить частичную инвариантность (инвариантность до ε). При этом повышается порядок астатизма системы и она становится инвариантной (не имеет ошибки) к определенным типам воздействий. Рассмотрим возможность компенсации ошибки на примере системы с комбинированным управлением по входному сигналу (рисунок 7.1, а). Предположим, что передаточная функция этой части содержит интегратор и несколько инерционных звеньев:
где Для выполнения условия инвариантности (2) передаточная функция компенсирующей цепи получается:
где
На выходе компенсирующей цепи формируется сигнал, пропорциональный производным входного сигнала, число которых определяется порядком знаменателя Реализовать компенсирующую цепь с передаточной функцией вида (3) практически не удается. При этом практически реализуемая передаточная функция компенсирующей цепи получается в виде
Наличие паразитной постоянной времени На практике обычно ограничиваются двумя-тремя производными из-за сложности реализации и настройки компенсирующей цепи. Хотя полная инвариантность при этом не достигается, но повышается астатизм системы на два-три порядка, причем без заметного ухудшения устойчивости.
Порядок выполнения лабораторной работы 1.1 Для схемы на рисунке 7.1,а принять 1.2 Собрать схему рисунка 7.1, а в программе VisSim без компенсирующей цепи 1.3 Собрать схему рисунка 1,а в программе VisSim с компенсирующей цепью 2.1 Для схемы на рисунке 7.1, б принять 2.2 Собрать схему в программе VisSim без компенсирующей цепи 2.3 Ввести
Содержание отчёта
1. Схемы исследования и результаты исследования. 2. Передаточные функции компенсирующих цепей, их вывод. 3. Выводы о влиянии компенсирующих цепей.
Контрольные вопросы
1. Что такое полная и частичная инвариантность? За счет чего она обеспечивается? 2. Исходя из каких условий выбирают передаточные функции компенсирующих цепей? 3. Если обеспечивается полная инвариантность системы, влияют ли компенсирующие цепи на устойчивость? Приложение – Таблица преобразований Лапласа
Литература 1. Теория автоматического управления: учебник для вузов / Л. С. Гольдфарб [и др.]; под ред. А. В. Нетушила. – 2-е изд. перераб. и доп. – Москва: Высшая школа, 1983. – 432 с. 2. Автоматическое регулирование. Теория и элементы систем: учебник для вузов / под ред. Н. Н. Иващенко – 3-е изд. – Москва: Машиностроение, 1973. – 606 с. 3. Анхимюк, В. Л. Теория автоматического управления: учеб. пособие для вузов / В. Л. Анхимюк, О. Ф. Опейко, Н. Н. Михеев – Минск: Дизайн ПРО, 2000. – 352 с. 4. Бесекерский, В. А., Теория автоматического регулирования / В. А. Бесекерский, Е. П. Попов. изд. 3-е, испр. – Москва: Наука, 1975. – 768 с 5. Куропаткин, А. В. Теория автоматического управления: учеб. пособие для электротехн. спец. вузов / А. В. Куропаткин; под ред. Д. В. Васильева. – Москва: Высшая школа, 1973. – 528 с. 6. Справочное пособие по теории систем автоматического регулирования и управления / под общ. ред. Е. А. Санковского. – Минск: Высшая школа, 1973. – 583 с. 7. Топчеев, Ю. И. Атлас для проектирования систем автоматического регулирования: учеб. пособие для вузов / Ю. И. Топчеев. – Москва: Машиностроение, 1989. – 752 с. 8. Микропроцессорные автоматические системы регулирования. Основы теории и элементы: учеб. пособие / В. В. Солодовников [и др.]; под ред. В. В. Солодовникова. – Москва: Высшая школа, 1991. – 256 с. 9. Руководство по проектированию систем автоматического управления: учеб. пособие для студентов специальности «Автоматика и теле- механика» / под ред. В. А. Бесекерского. – Москва: Высшая школа, 1983. – 296 с. 10. Кулаков, Г. Е. Анализ и синтез систем автоматического регулирования / Г. Е. Кулаков. – Минск: УП Технопринт, 2003. – 125 с. 11. Лазарева, Т. Я. Основы теории автоматического управления: учеб. пособие / Т. Я. Лазарева, Ю. Ф. Мартемьянов. – Тамбов: Изд-во Тамбовского государственного технологического университета, 2003. – 308 с. 12. Андриевский, Б. Р. Избранные главы теории автоматического управления с примерами на языке Matlab / Б. Р. Андриевский, А. Л. Фрадков. – Санкт-Петербург: Наука, 2000. – 475 с. 13. Клиначев, Н. В. Теория систем автоматического регулирования. Учебно-методический комплекс, 2005. Электронный ресурс.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1173; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.01 с.) |

 . Тогда КУ можно реализовать при помощи R, C, L – элементов.
. Тогда КУ можно реализовать при помощи R, C, L – элементов.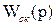 ).
).
 , где
, где  – передаточная функция исходной системы.
– передаточная функция исходной системы. , где
, где  – передаточная функция участка системы к которому подключено КУ.
– передаточная функция участка системы к которому подключено КУ. – передаточная функция участка системы от сумматора до выхода системы.
– передаточная функция участка системы от сумматора до выхода системы.
 ,
, – передаточная функция участка цепи не охваченного ОС.
– передаточная функция участка цепи не охваченного ОС. – передаточная функция элементов охваченных местной ОС.
– передаточная функция элементов охваченных местной ОС.
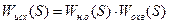

 → последовательное КУ через КУ обратной связи.
→ последовательное КУ через КУ обратной связи. → КУ обратной связи через КУ последовательного типа.
→ КУ обратной связи через КУ последовательного типа.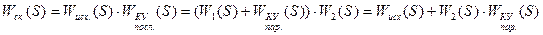


 – сопротивления участков цепи, записанные в операторной форме.
– сопротивления участков цепи, записанные в операторной форме.
 – изодромное звено,
– изодромное звено, – время изодрома.
– время изодрома.

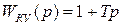 - форсирующее звено.
- форсирующее звено. .
. .
.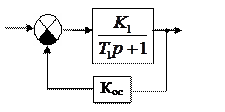


 , при
, при 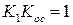
 , т.е. вводится интегрирование на базе апериодического звена.
, т.е. вводится интегрирование на базе апериодического звена.
 T>>Ti, т.е. больше постоянных времени остальных звеньев.
T>>Ti, т.е. больше постоянных времени остальных звеньев.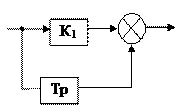
 , где
, где 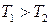 ,
,  . В этом случае положительный фазовый сдвиг получается за счет подавления низких частот. Аналогичный эффект дает применение отрицательных ОС, содержащих апериодическое звено.
. В этом случае положительный фазовый сдвиг получается за счет подавления низких частот. Аналогичный эффект дает применение отрицательных ОС, содержащих апериодическое звено.


 .
.
 ,
,  ,
,  ,
,  ,
,  .
. (порядок системы, структурно устойчива или нет, статическая или астатическая).
(порядок системы, структурно устойчива или нет, статическая или астатическая). и
и 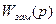 без КУ ОС, записать характеристическое уравнение и условия устойчивости, оценить устойчивость при выбранных параметрах звеньев.
без КУ ОС, записать характеристическое уравнение и условия устойчивости, оценить устойчивость при выбранных параметрах звеньев. .
. ;
;  ;
;  . Оценить влияние
. Оценить влияние  . Определить наличие ошибки, используя теорему о предельном переходе. Оценить влияние величины
. Определить наличие ошибки, используя теорему о предельном переходе. Оценить влияние величины 

 . Необходимо записать характеристическое уравнение замкнутого контура и определить условие устойчивости.
. Необходимо записать характеристическое уравнение замкнутого контура и определить условие устойчивости. при
при 

 , при введении которой можно получить абсолютную инвариантность системы как по входному сигналу, так и по возмущению, т. е. абсолютно точную систему, в которой ошибка равна нулю и не зависит от входного сигнала и возмущения.
, при введении которой можно получить абсолютную инвариантность системы как по входному сигналу, так и по возмущению, т. е. абсолютно точную систему, в которой ошибка равна нулю и не зависит от входного сигнала и возмущения. (1)
(1) в этом случае будет тождественно равна единице:
в этом случае будет тождественно равна единице: .
. .
. и
и  , обусловленные возмущением, будут равны, а их разность (на входе
, обусловленные возмущением, будут равны, а их разность (на входе  ) равна нулю, т. е. действия возмущения по цепям
) равна нулю, т. е. действия возмущения по цепям  взаимно компенсируются.
взаимно компенсируются.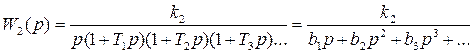 ,
, ;
;  ;
;  ;…
;… , (3)
, (3) ;
;  ;
;  ;…
;… .
.
 в передаточной функции
в передаточной функции  влияет на условия компенсации ошибки, а также на характеристическое уравнение замкнутой системы. Поэтому на практике необходимо, чтобы
влияет на условия компенсации ошибки, а также на характеристическое уравнение замкнутой системы. Поэтому на практике необходимо, чтобы  и
и  . Записать для данной схемы условие полной инвариантности по задающему воздействию и найти
. Записать для данной схемы условие полной инвариантности по задающему воздействию и найти  .
.


 . Записать для данной схемы условие полной инвариантности по возмущающему воздействию и найти
. Записать для данной схемы условие полной инвариантности по возмущающему воздействию и найти  .
. .
.