
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория автоматического управленияСодержание книги
Поиск на нашем сайте
В.И. Гаркушенко
ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ Практическое руководство к выполнению курсовой работы
Казань 2010
УДК 681.51
Гаркушенко В.И. Теория автоматического управления: Практическое руководство к выполнению курсовой работы: Казань, 2010. 95с.
Пособие предназначено для выполнения курсовой работы по дисциплине «Теория автоматического управления» с использованием современного вычислительного пакета MATLAB 7.5. Представленные в пособии программные файлы системы MATLAB 7.5. позволяют автоматизировать наиболее трудоемкие вычислительные операции, освобождая тем самым время для более полного теоретического исследования с использованием различных методов и расширения задачи синтеза, включающей синтез непрерывного и дискретного регуляторов. Предназначено для студентов очного и заочного отделений специальностей 210100 – «Управление и информатика в технических системах», 181200 — «Приборы и системы ориентации, стабилизации и навигации», а также может быть использовано для других инженерных специальностей технических вузов.
Табл. 5. Ил. 47. Библиогр.: 31 назв.
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ. 4 1. ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ.. 5 1.1 Cиловые системы автоматического управления. 5 1.1.1 Исходные данные. 8 1.1.2 Техническое задание. 10 1.2 Содержание пояснительной записки. 11 2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.. 12 2.1 Расчет САУ в линейном приближении. 13 2.2 Расчет САУ с учетом нелинейности. 15 3. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ.. 16 3.1 Введение. 16 3.2 Математическое описание функциональных элементов. 21 3.2.1 Генератор постоянного тока. 22 3.2.2 Тахогенератор. 24 3.2.3 Электромашинный усилитель. 25 3.2.4 Двигатель постоянного тока. 30 3.3 Определение передаточных функций замкнутых систем. 31 3.4 Определения коэффициента усиления электронного усилителя. 34 3.5 Построение области устойчивости по коэффициенту усиления. 35 3.5.1 Алгебраический метод построения области устойчивости. 35 3.5.2 Частотный метод построения области устойчивости. 37 3.6 Построение ЛАХ и ЛФХ разомкнутой системы и определение запасов устойчивости замкнутой системы.. 41 3.7 Построение переходной характеристики замкнутой системы.. 49 3.8 Синтез последовательной коррекции с помощью ЛАХ и ЛФХ.. 50 3.9 Электрическая схема корректирующего устройства. 63 3.10 Синтез дискретного корректирующего устройства. 66 3.10.1 Приближенный синтез дискретного корректирующего устройства. 67 3.10.2 Синтез дискретного корректирующего устройства частотным методом. 71 3.11 Определение параметров автоколебаний. 78 3.12 Исследование системы на абсолютную устойчивость. 84 СПИСОК ЛИТЕРАТУРЫ.. 88 ПРИЛОЖЕНИЕ А. Корректирующие цепи. 90 ПРИЛОЖЕНИЕ Б. Коэффициенты гармонической линеаризации нелинейных характеристик. 93 ПРИЛОЖЕНИЕ В. Справочные данные. 95 ВВЕДЕНИЕ
В связи с повышением требований к уровню подготовки специалиста и широким использованием современных вычислительных средств, в практическом руководстве переработаны и дополнены методические указания по статическому и динамическому расчету одномерных типовых САУ, используемых в учебном процессе на кафедре «Автоматика и управление» [28, 29]. Пособие предназначено для самостоятельной работы студентов очного и заочного отделений специальностей 210100 – «Управление и информатика в технических системах», 181200 — «Приборы и системы ориентации, стабилизации и навигации», а также может быть использовано для других инженерных специальностей технических вузов.. Целью практического руководства является закрепление теоретических знаний по дисциплине «Теория автоматического управления» и приобретение практических навыков по проектированию САУ с использованием современного вычислительного пакета MATLAB 7.5. Для облегчения самостоятельной работы по каждому пункту задания приводятся постраничные ссылки на литературу, при этом для выполнения расчетов в курсовой работе не требуется дополнительных сведений. Представленные в пособии программные файлы системы MATLAB 7.5. позволяют автоматизировать наиболее трудоемкие вычислительные операции, освобождая тем самым время для более полного теоретического исследования с использованием различных методов и расширения задачи синтеза, включающей синтез непрерывного и дискретного регуляторов. Учитывая, что программные средства системы MATLAB являются вспомогательными для выполнения курсовой работы, необходимые программные файлы могут быть скопированы из электронной версии пособия, а также взяты из его приложения.
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Шифр задания на курсовую работу состоит из первой буквы и трех групп цифр, при этом буква означает тип принципиальной схемы одномерной САУ (рис.1-5). Первая группа из четырех цифр означает: первая цифра - № двигателя; вторая цифра – № генератора; третья цифра – № электромашинного усилителя; четвертая цифра – № тахогенератора (таблица 1). Цифра "0" указывает на отсутствие элемента в данной схеме. Вторая группа из трех цифр означает: первая цифра – число, на которое надо поделить значение в первом столбце таблицы 2; вторая цифра – число, которое надо отнять от значения во втором столбце таблицы 2; третья цифра – число, на которое надо поделить значение в третьем столбце таблицы 2. Третья группа из двух цифр, предназначенная для выполнения второй части задания, означает: первая цифра – № нелинейности (рис.6); вторая цифра – число, на которое надо умножить заданное значение параметра Например, для выполнения задания А-1323-202-12 необходимо рассчитать схему А с двигателем № I, с генератором № 3, с электромашинным усилителем №2, с тахогенератором № 3; в соответствии с обозначениями таблицы 2 Исходные данные
Номинальные данные электрических машин постоянного тока представлены в таблице 1. Таблица 1. Номинальные данные электрических машин постоянного тока
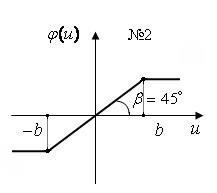
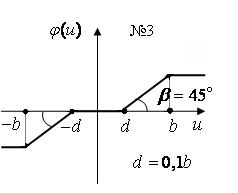
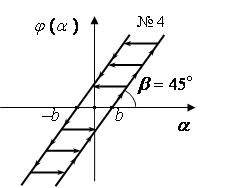
При рассмотрении схем необходимо учесть следующее: 1) Кривые намагничивания всех электрических машин предполагаются линейными в пределах рабочего режима заданных систем, гистерезис отсутствует, реакции электрических машин скомпенсированы. 2) Пренебрежимо малы индуктивности обмоток якорей всех машин. 3) Параметры короткозамкнутой цепи ЭМУ равны 4) Момент инерции ротора двигателя 5) Электронный усилитель с коэффициентом усиления 6) Параметры корректирующей 7) В схеме В сопротивления делителя напряжения 8) В схеме Б параметры управляющей обмотки возбуждения ЭМУ и обмотки обратной связи считать одинаковыми ( для стабилизирующего трансформатора со стальным сердечником приняты следующие параметры: первичная обмотка – вторичная обмотка – взаимная индукция обмоток 9) В схемах Г и Д коэффициенты передачи дифференциала и потенциометра соответственно равны 10) В схеме Д параметры делителя напряжения 11) В схемах Г и Д передаточные отношения редуктора 12) При исследовании влияния нелинейностей на динамику замкнутой системы с найденным законом управления рассматриваются нелинейные элементы с нечетно-симметричными характеристиками № 1,2,3 (рис. 6), включаемые в структурную схему системы перед электронным усилителем и нелинейный элемент № 4 только для схем Г, Д, включаемый перед редуктором двигателя. Здесь нелинейный элемент № 1 типа "зона нечувствительности" характеризует момент трогания двигателя для схем А, Б, Г, Д с параметром
Рис. 6.
1.1.2 Техническое задание
1. По заданным в соответствии с таблицей 2 показателям точности и качества переходных процессов в замкнутой САУ провести синтез непрерывной последовательной коррекции, составить ее электрическую схему, определить параметры корректирующего устройства и место его включения. Таблица 2. Требуемые показатели точности и качества
Здесь показатели качества Для схем А, Б, В значение командного сигнала Для схем А, Б, Г, Д момент нагрузки 2. Рассмотреть возможность замены непрерывной коррекции на дискретное корректирующее устройство при малых периодах дискретности. 3. Провести анализ влияния нелинейного элемента на динамику замкнутой системы при отсутствии входного сигнала и нагрузки с использованием метода гармонической линеаризации или метода абсолютной устойчивости.
Содержание пояснительной записки
Пояснительная записка (объемом не более 40 страниц) оформляется в соответствии с ГОСТ 7.32-2001 [31]. Рекомендуется оформление работы в Microsoft Word с использованием электронной версии данного пособия, с набором математических формул в редакторе Math Type 5.2, который прилагается к электронной версии данного пособия наряду с другими литературными источниками. Пояснительная записка содержит: · титульный лист (с названием задания и его шифром); · содержание; · введение; · основная часть; · заключение; · список использованных источников; · приложения. В пояснительной записке приводятся результаты расчетов в соответствии с порядком выполнения работы, описанного в разделе 2. При этом названия пунктов выполнения работы, выделенных курсором, входят в содержание пояснительной записки. В заключении приводятся основные результаты, полученные в работе. В приложение рекомендуется выносить программы расчета на выбранном алгоритмическом языке, схемы моделирования (например, в системах MATLAB, SIMULINK), графики логарифмических характеристик и т.п. Переходные процессы, иллюстрирующие результаты вычислений, следует приводить в тексте основной части пояснительной записки.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Введение. Во введении необходимо привести: · схему системы управления, исходные данные в соответствии с шифром задания и принятыми допущениями в п.п.1.2; · краткое описание работы схемы; · функциональную схему системы; · классификацию по принципу регулирования [2, с.21-34; 3, с.9-14; 4, с.30]; · определение статизма (астатизма) системы по отношению к возмущению нагрузки и команде вида I. Расчет САУ в линейном приближении II. Расчет САУ с учетом нелинейности На первом этапе проводится расчет САУ в линейном приближении без учета имеющихся нелинейностей; на втором этапе – расчет системы при наличии одного нелинейного элемента. Расчеты проводятся с использование ПЭВМ. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ Введение
Во введении при доказательстве статизма или астатизма системы можно воспользоваться методом доказательства от противного. Например, для схемы А по отношению к входному сигналу При доказательстве статизма системы по отношению к возмущению рассматривается изменение установившейся ошибки при наличии входного сигнала Для пояснения работы системы и обоснования преимущества отрицательной обратной связи необходимо учитывать следующее. 1. Для систем стабилизации (схемы А, Б, В) обобщенная структурная схема системы для установившегося режима системы, т.е. без учета инерционности функциональных элементов (постоянные времени типовых звеньев равны нулю) представлена на рис. 7.
Выражение для управляемой выходной координаты системы
где Преимущество замкнутой системы, заключается в том, что выход Желаемое значение выхода
Тогда ошибка стабилизации заданного значения
т.е. зависит от заранее неизвестного возмущения С другой стороны ошибка рассогласования
которая при Здесь также при некотором значении Таким образом, при возможности измерения и формирования входного сигнала В тех случаях, когда постоянный сигнал 2. Для следящих систем (схемы Г, Д) обобщенная структурная схема системы без учета инерционности функциональных элементов (постоянные времени типовых звеньев равны нулю) представлена на рис. 8.
Здесь переменный входной сигнал Если для функции
При этом время регулирования следящей системы
или после упрощения
Для устойчивой замкнутой системы установившаяся ошибка определяется по формуле
где В системах слежения за подвижными объектами должно выполняться условие
определяется по формуле
Генератор постоянного тока
1. Уравнения статики для номинального режима генератора имеют вид
где Отсюда следует, что
и с учетом паспортных значений найдем коэффициент усиления генератора
Например, для генератора №1 получим
2. Уравнения динамики генератора в схеме соединения имеют вид
где Отсюда с учетом преобразования Лапласа при нулевых начальных условиях получим
где Например, коэффициент усиления генератора для схем Г, Д имеет значение
т.е. меньше паспортного значения. 3. Для генератора с нагрузкой
где
В установившемся номинальном режиме при отсутствии нагрузки
Учитывая малость величины
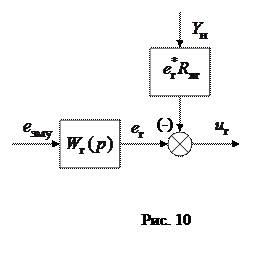
Фрагмент структурной схемы генератора с нагрузкой представлен на рис. 10.
Тахогенератор
1. Тахогенератор постоянного тока предназначен для измерения угловой скорости вращения якоря. Уравнения статики для номинального режима следуют из уравнений статики генератора без учета малого сопротивления
где Отсюда следует, что
где
Например, для тахогенератора №1 получим
2. Уравнения динамики тахогенератора имеют вид
Тогда передаточная функция тахогенератора для схем А,Б имеет вид
Для схем Г, Д выходом тахогенератора является угловое перемещение
Электромашинный усилитель
1. С учетом принятых допущений о полной компенсации реакции якоря в цепи нагрузки ЭМУ, уравнения статики для номинального режима имеют вид
где Исключая переменные
Отсюда найдем
Например, для ЭМУ №1 получим
2. Уравнения динамики ЭМУ в схеме соединения имеют вид
где Отсюда с учетом преобразования Лапласа при нулевых начальных условиях найдем: 1) для схем А, В:
с передаточной функцией
где 2) в схемах Б, В предусмотрена гибкая дифференцирующая обратная связь, предназначенная для гашения возможных колебательных процессов в электромашинной системе при больших коэффициентах усиления ЭМУ. Сигнал отрицательной обратной связи снимается с зажимов выхода ЭМУ в соответствии со схемой
где
Например, для генератора и ЭМУ №1 получим
а) В схеме Б обратная связь осуществляется с помощью стабилизирующего трансформатора, уравнения которого имеют вид [8, стр.68; 9, стр. 17]
где Исключая ток
где После подстановки исходных данных полученное выражение можно представить в виде
где наименьшей постоянной времени
С учетом обратной связи по току
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.51.35 (0.009 с.) |

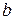 .
.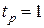 с,
с, 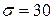 %,
%, 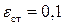 В; в задании на нелинейную часть использовать нелинейность № 1 с параметром
В; в задании на нелинейную часть использовать нелинейность № 1 с параметром 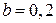 В.
В.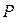 кВт
кВт
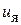 В
В
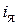 А
А
 А
А
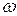 рад/с
рад/с
 кг×м2
кг×м2
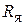 Ом
Ом
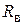 Ом
Ом
 Гн
Гн
 Ом;
Ом; 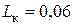 Гн.
Гн.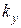 считается идеальным с бесконечным входным сопротивлением и выходным сопротивлением R вых=10 Ом.
считается идеальным с бесконечным входным сопротивлением и выходным сопротивлением R вых=10 Ом.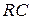 - цепи (в схемах А, В):
- цепи (в схемах А, В):  =4000 Ом,
=4000 Ом,  Ом,
Ом, 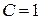 мкФ.
мкФ.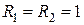 кОм; сопротивление нагрузки
кОм; сопротивление нагрузки 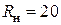 Ом.
Ом.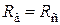 ,
,  ,
,  );
); Ом,
Ом, 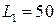 Гн;
Гн;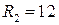 Ом,
Ом, 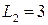 Гн;
Гн;  Ом (дополнительное сопротивление);
Ом (дополнительное сопротивление); .
. =1,
=1, 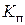 =114,6 В/рад.
=114,6 В/рад. кОм,
кОм,  кОм.
кОм. и платформы
и платформы 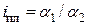 соответственно равны
соответственно равны 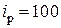 ,
, 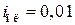 .
.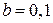 В; нелинейный элемент № 2 типа "насыщение" определяет ограничение управляющего напряжения на выходе электронного усилителя, связанного с величиной напряжения питания, с параметром
В; нелинейный элемент № 2 типа "насыщение" определяет ограничение управляющего напряжения на выходе электронного усилителя, связанного с величиной напряжения питания, с параметром 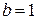 0 В; нелинейный элемент № 3 типа "зона нечувствительности - насыщение" сочетает свойства двух первых нелинейных элементов с параметром
0 В; нелинейный элемент № 3 типа "зона нечувствительности - насыщение" сочетает свойства двух первых нелинейных элементов с параметром 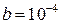 рад.
рад.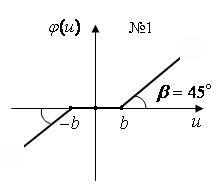
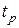 , с
, с
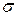 , %
, %
 и возмущению
и возмущению 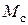 )
)
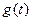 )
)
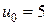 В; для схем Г, Д командный сигнал
В; для схем Г, Д командный сигнал 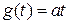 ,
, 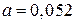 рад/с.
рад/с.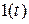 ,
, 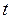 (и
(и  для схем Г, Д) методом от противного. Расчет САУ состоит из двух этапов:
для схем Г, Д) методом от противного. Расчет САУ состоит из двух этапов: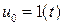 и при отсутствии нагрузки предположим, что система является астатической, т.е. в установившемся режиме рассогласование
и при отсутствии нагрузки предположим, что система является астатической, т.е. в установившемся режиме рассогласование 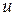 равно нулю. Тогда на выходе усилителя напряжение отсутствует и на двигатель напряжение не поступает, и ротор неподвижен. В этом случае рассогласование
равно нулю. Тогда на выходе усилителя напряжение отсутствует и на двигатель напряжение не поступает, и ротор неподвижен. В этом случае рассогласование 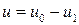 между входным сигналом
между входным сигналом 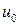 и нулевым напряжением на выходе тахогенератора
и нулевым напряжением на выходе тахогенератора 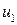 равно
равно 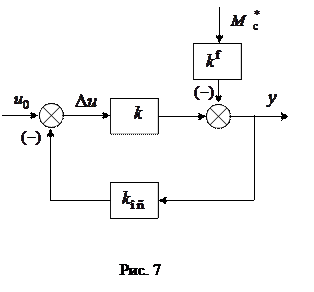
 в установившемся режиме при постоянных значениях входного сигнала
в установившемся режиме при постоянных значениях входного сигнала  для разомкнутой и замкнутой системы имеют вид
для разомкнутой и замкнутой системы имеют вид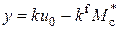 ,
,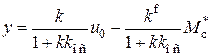 ,
,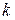 и
и 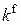 – коэффициенты передачи системы,
– коэффициенты передачи системы, 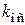 – коэффициент обратной связи.
– коэффициент обратной связи. в замкнутой системе
в замкнутой системе  .
.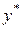 для разомкнутой и замкнутой системы может быть достигнуто заданием входного сигнала
для разомкнутой и замкнутой системы может быть достигнуто заданием входного сигнала 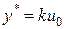 ;
; .
.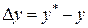 имеет вид
имеет вид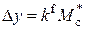 ;
; ,
,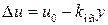 для замкнутой системы определяется по формуле
для замкнутой системы определяется по формуле ,
, должна быть равна
должна быть равна 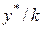 , т.е. не равной нулю. Кроме того для простоты реализации коэффициент
, т.е. не равной нулю. Кроме того для простоты реализации коэффициент 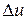 на динамику системы может оказывать влияние нелинейность типа "зона нечувствительности".
на динамику системы может оказывать влияние нелинейность типа "зона нечувствительности". .
.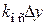 .
.
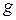 заранее неизвестен и измеряемая ошибка рассогласования
заранее неизвестен и измеряемая ошибка рассогласования  характеризует точность слежения системы.
характеризует точность слежения системы.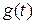 удается провести кусочно-линейную аппроксимацию
удается провести кусочно-линейную аппроксимацию  с заданной точностью (рис. 9), то на интервалах времени
с заданной точностью (рис. 9), то на интервалах времени  задающий сигнал
задающий сигнал  , где постоянные коэффициенты
, где постоянные коэффициенты 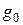 ,
, 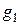 заранее неизвестны.
заранее неизвестны.
 должно удовлетворять условию
должно удовлетворять условию 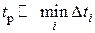 , а заданная точность слежения должна достигаться для
, а заданная точность слежения должна достигаться для  , поскольку на постоянное воздействие
, поскольку на постоянное воздействие 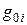 ошибка равна нулю. Это следует из выражения изображение по Лапласу для ошибки
ошибка равна нулю. Это следует из выражения изображение по Лапласу для ошибки 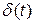 :
: ,
,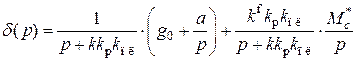 .
.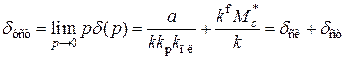 ,
,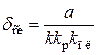 – скоростная ошибка;
– скоростная ошибка;  – статическая ошибка. При этом скорость командного сигнала равна установившейся скорости регулируемой координаты
– статическая ошибка. При этом скорость командного сигнала равна установившейся скорости регулируемой координаты 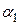 , т.е.
, т.е.  . Отсюда следует, что
. Отсюда следует, что 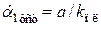 .
.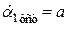 ,
, 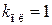 ; в системах воспроизведения командного сигнала возможны случаи
; в системах воспроизведения командного сигнала возможны случаи  ,
, 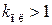 или
или 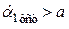 ,
, 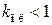 . При этом установившаяся ошибка слежения
. При этом установившаяся ошибка слежения 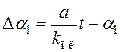 с учетом выражения
с учетом выражения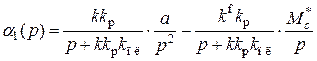
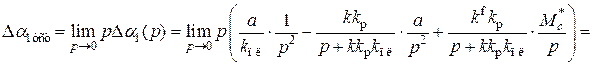
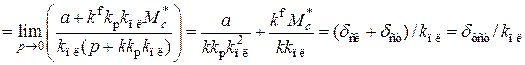 .
.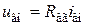 ,
,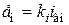 ,
,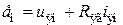 ,
, и
и 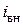 – номинальные напряжение и ток в обмотке возбуждения генератора,
– номинальные напряжение и ток в обмотке возбуждения генератора, 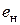 – номинальное значение э.д.с.;
– номинальное значение э.д.с.; 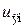 и
и 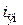 – номинальные напряжение и ток в якорной обмотке генератора,
– номинальные напряжение и ток в якорной обмотке генератора,  – сопротивление управляющей обмотки возбуждения генератора;
– сопротивление управляющей обмотки возбуждения генератора;  – сопротивление якорной обмотки генератора;
– сопротивление якорной обмотки генератора; 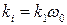 – коэффициент усиления по току, зависящий от угловой скорости вращения
– коэффициент усиления по току, зависящий от угловой скорости вращения 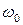 якоря вспомогательного двигателя. В генераторах, предназначенных для усиления напряжения по мощности,
якоря вспомогательного двигателя. В генераторах, предназначенных для усиления напряжения по мощности, 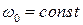 .
.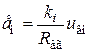 ,
,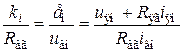 .
. .
.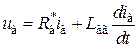 ,
,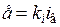 ,
, ,
,  ,
, 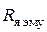 – сопротивление якоря ЭМУ – для схем А, Б, В;
– сопротивление якоря ЭМУ – для схем А, Б, В;  ,
, 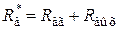 ,
, 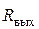 – выходное сопротивление электронного усилителя – для схем Г, Д.
– выходное сопротивление электронного усилителя – для схем Г, Д.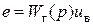 с передаточной функцией
с передаточной функцией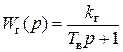 ,
,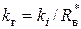 ,
,  .
.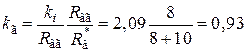 ,
, в схеме В напряжение на нагрузке определяется по формуле
в схеме В напряжение на нагрузке определяется по формуле ,
, ;
; 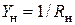 – проводимость нагрузки. Отсюда следует, что напряжение
– проводимость нагрузки. Отсюда следует, что напряжение 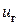 является нелинейной функцией от величин
является нелинейной функцией от величин  ,
, 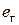 . Учитывая, что при наличии нагрузки
. Учитывая, что при наличии нагрузки  , с помощью разложения в ряд Тейлора можно записать
, с помощью разложения в ряд Тейлора можно записать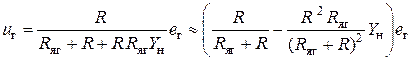 .
.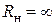 (
( ) справедливо уравнение
) справедливо уравнение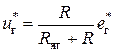 .
. , отклонения
, отклонения 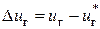 ,
, 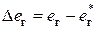 вызванные подключением нагрузки
вызванные подключением нагрузки 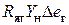 будет справедливо уравнение
будет справедливо уравнение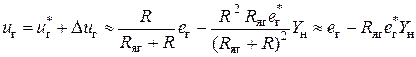 .
.
 ,
,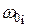 – номинальные обороты якоря;
– номинальные обороты якоря; 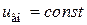 .
.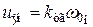 ,
,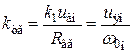 .
.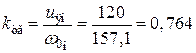 Вс/рад.
Вс/рад.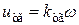 .
. .
.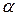 . В этом случае с учетом равенства
. В этом случае с учетом равенства 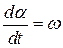 получим
получим .
. ,
, ,
,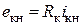 ,
, ,
,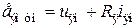 ,
,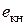 и
и 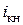 – номинальные э.д.с. и ток в короткозамкнутой цепи;
– номинальные э.д.с. и ток в короткозамкнутой цепи; 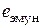 ,
, 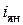 и
и  – номинальные э.д.с., напряжение, ток и сопротивление якорной цепи нагрузки ЭМУ соответственно;
– номинальные э.д.с., напряжение, ток и сопротивление якорной цепи нагрузки ЭМУ соответственно; 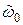 – постоянная угловая скорость вращения якоря вспомогательного двигателя.
– постоянная угловая скорость вращения якоря вспомогательного двигателя. .
.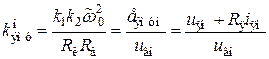 .
.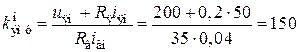 .
. ,
,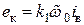 – для схем А, В;
– для схем А, В; – для схемы Б (объяснить почему),
– для схемы Б (объяснить почему), ,
,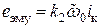 ,
,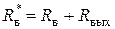 ,
, 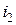 – ток во вторичной обмотке трансформатора схемы Б.
– ток во вторичной обмотке трансформатора схемы Б.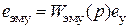
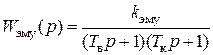 ,
,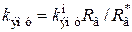 ,
, 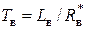 ,
, 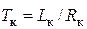 .
.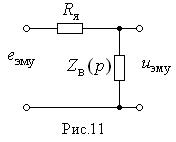 рис.11, где
рис.11, где 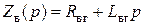 – операционное сопротивление обмотки возбуждения генератора. При этом
– операционное сопротивление обмотки возбуждения генератора. При этом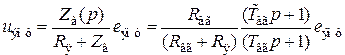 ,
,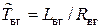 ,
, 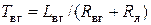 . Учитывая, что
. Учитывая, что 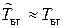 , можно принять
, можно принять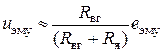 .
.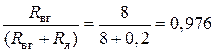 .
.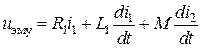 ,
,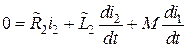 ,
,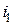 и
и 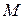 – взаимная индукция обмоток;
– взаимная индукция обмоток; 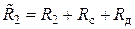 – общее сопротивление вторичной обмотки,
– общее сопротивление вторичной обмотки, 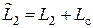 – общее индуктивное сопротивление вторичной обмотки.
– общее индуктивное сопротивление вторичной обмотки. для трансформатора со стальным сердечником получим выражение для тока
для трансформатора со стальным сердечником получим выражение для тока  ,
,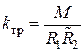 ,
, 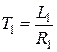 ,
,  .
.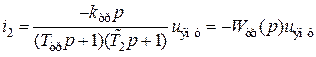 ,
,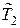 можно пренебречь. Тогда упрощенная передаточная функция трансформатора будет иметь вид:
можно пренебречь. Тогда упрощенная передаточная функция трансформатора будет иметь вид: .
.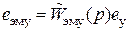 , где эквивалентная передаточная фун
, где эквивалентная передаточная фун 


