
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез дискретного корректирующего устройства частотным методомСодержание книги
Поиск на нашем сайте
В случае, когда с помощью приближенного способа синтез дискретного корректирующего устройства удается получить требуемое качество переходной характеристики замкнутой системы только при малом значении периода дискретности Последовательность синтеза дискретной коррекции следующая [9, с. 66-70]. 1. По передаточной функции нескорректированной разомкнутой системы
с учетом передаточной функции фиксатора нулевого порядка
2. С помощью подстановки
осуществляет конформное отображение замкнутой области устойчивости корней
Рис. 35
Действительно, учитывая, что любому корню
С другой стороны, поскольку
где псевдочастота Отсюда следует, что единичная окружность отображается в мнимую ось комплексной Для найденной передаточной функции 3. Проводится факторизация: передаточной функции
где символы "+" и "–" обозначают полиномы, корни которых удовлетворяют и не удовлетворяют требуемым показателям соответственно. Формируется структура желаемой передаточной функции
Таким образом, желаемая передаточная должна содержать полиномы 4. По передаточной функции 5. С учетом свободы выбора полиномов
6. Определяется передаточная функция последовательной дискретной коррекции по ее логарифмической характеристике
или с помощью выражения
Выражение передаточной функции дикретной коррекции 7. По найденной передаточной функции
Данной передаточной функции соответствует операторное уравнение для дискретной коррекции
которому соответствует разностное уравнение
при нулевых начальных условиях:
Для устойчивой работы алгоритма вычисления Таким образом, алгоритм вычисления управляющего сигнала Влияние запаздывания на качество переходных процессов замкнутой системы можно оценить с помощью моделирования системы. При необходимости следует заново провести синтез коррекции с учетом запаздывания
Для рассмотренного выше примера при % Передаточная функция нескорректированной разомкнутой системы Wpas=75.5*tf([0.4 1],[0.04 1])*tf([1],[0.2 1])*... tf([1],[0.96 1])*tf([1],[0.38 1]);
% Дискретная передаточная функция нескорректированной разомкнутой системы T0=0.06, Wpasd=c2d(Wpas,T0); % ЛАХ и ЛФХ нескорректированной дискретной системы в псевдочастоте [nWpasd,dWpasd]=tfdata(Wpasd,'v'); NWpasd=poly2sym(nWpasd,'z'); DWpasd=poly2sym(dWpasd,'z'); s=sym('s'); z=(1+s*T0/2)/(1-s*T0/2); Ns=compose(NWpasd,z); Ds=compose(DWpasd,z); Ws=Ns/Ds; Ws=simple((Ws)); [nWs,dWs]=numden(Ws); nWs=sym2poly(expand(nWs));dWs=sym2poly(expand(dWs)); Wpass=tf(nWs,dWs);zpk(Wpass) % Асимптотическая ЛАХ нескорректированной системы в псевдочастоте omega=[0.1 1.041 2.495 2.626 4.963 21.17 33.33 46.17 79.54 1000]; L1=20*log10(75.5);L2=20*log10(75.5);L3=L2-20*log10(2.495/1.041); L4=L3;L5=L4-20*log10(4.963/2.626);L6=L5-40*log10(21.17/4.963); L7=L6-60*log10(33.33/21.17);L8=L7-40*log10(46.17/33.33); L9=L8-20*log10(79.54/46.17);L10=L9; L=[L1 L2 L3 L4 L5 L6 L7 L8 L9 L10]; figure(1); semilogx(omega,L);hold on % Асимптотическая ЛАХ желаемой разомкнутой системы в псевдочастоте omega=[0.1 0.6 3 46.17 79.54 1000]; L1=20*log10(75.5);L2=20*log10(75.5);L3=L2-40*log10(4/0.7); L4=L3-20*log10(46.17/4);L5=L4-20*log10(79.54/46.17);L6=L5; L=[L1 L2 L3 L4 L5 L6]; semilogx(omega,L,'r');grid on % красный цвет % Точные ЛАХ и ЛФХ, запасы устойчивости желаемой системы в псевдочастоте Wgs=75.5*tf([1/3 1],[1/0.6 1])*tf([1/46.17 1],[1/0.6 1])... *tf([1/33.33 -1],[1/33.33 1])*tf([1/79.54 -1],[1/79.54 1]);zpk(Wgs) figure(2);margin(Wgs); % Последовательная коррекция в псевдочастоте Wks=Wgs/Wpass;Wks=minreal(Wks,1e-2); % Обратный переход от псевдочастоты к z-изображению [nWks,dWks]=tfdata(Wks,'v'); NWks=poly2sym(nWks,'s'); DWks=poly2sym(dWks,'s'); z=sym('z'); s=2/T0*(z-1)/(z+1); Ns=compose(NWks,s); Ds=compose(DWks,s); Ws=Ns/Ds; Ws=simple((Ws)); [nWs,dWs]=numden(Ws); nWs=sym2poly(expand(nWs));dWs=sym2poly(expand(dWs)); % Дискретная коррекция в z-изображении Wkd=tf(nWs,dWs,T0);zpk(Wkd) sim('DiskrKor');figure(3);hold on; simplot(y)
В результате выполнения программы определяются передаточные функции
Zero/pole/gain: 0.071012 (s-79.54) (s-33.33) (s+46.17) (s+2.495) ------------------------------------------------ (s+21.17) (s+4.963) (s+2.626) (s+1.041)
Zero/pole/gain: 0.19623 (s-79.54) (s-33.33) (s+46.17) (s+3) ------------------------------------------- (s+79.54) (s+33.33) (s+0.6)^2 Zero/pole/gain: 0.8345 (z-0.9394) (z-0.8539) (z-0.8349) (z-0.7408) (z-0.2231) ------------------------------------------------------------- (z-0.9646)^2 (z-0.8607) (z+0.4094) (z-5e-005)
Sampling time: 0.06
Задание желаемой передаточной функции разомкнутой системы в псевдочастоте проводится с учетом В результате выполнения программы также выводятся на печать: асимптотические ЛАХ нескорректированной и желаемой разомкнутой системы в псевдочастоте (рис. 36); точные значения ЛАХ и ЛФХ желаемой разомкнутой системы (рис. 37) с указанием запасов по амплитуде (8,26 дБ) и фазе (45,5 рад/с); переходная характеристика замкнутой системы (рис. 38) с показателями качества
Рис. 36
С учетом малости полюса
При этом переходная характеристика замкнутой системы практически не изменяется. Здесь полюса передаточной функции
Рис. 37
Рис. 38 Для вычисления управляющего сигнала Оценим влияние запаздывания управляющего сигнала
Wpas=75.5*tf([0.4 1],[0.04 1])*tf([1],[0.2 1])*... tf([1],[0.96 1])*tf([1],[0.38 1],'td',0.001) Wkd=tf(nWs,dWs,T0);zpk(Wkd) sim('DiskrKor');figure(3);hold on; simplot(y)
который запускается на выполнение после выполнения предыдущего Script-файла. В результате строится переходная характеристика замкнутой системы с показателями качества
|
|||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.150.165 (0.007 с.) |

 с, можно провести синтез дискретной коррекции с помощью логарифмических частотных характеристик.
с, можно провести синтез дискретной коррекции с помощью логарифмических частотных характеристик.
 строится ее дискретная передаточная функция по формуле:
строится ее дискретная передаточная функция по формуле: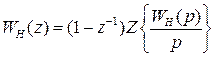 .
.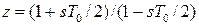 находятся передаточные функции
находятся передаточные функции  ,
,  , где
, где 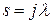 ,
,  – псевдочастота. При
– псевдочастота. При  билинейное преобразование
билинейное преобразование .
. комплексной плоскости
комплексной плоскости  в левую полуплоскость
в левую полуплоскость  вспомогательной комплексной переменной
вспомогательной комплексной переменной  (рис. 35) или переменной
(рис. 35) или переменной 

 соответствует единственный корень
соответствует единственный корень  , при
, при  будет выполняться неравенство
будет выполняться неравенство .
. , с учетом равенства
, с учетом равенства  при
при  получим
получим ,
, изменяется на интервале
изменяется на интервале  при изменении
при изменении  . При малых значениях
. При малых значениях 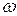 псевдочастота
псевдочастота  , т.к.
, т.к.  .
.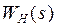 разомкнутой системы можно применить критерий устойчивости Найквиста для непрерывных систем.
разомкнутой системы можно применить критерий устойчивости Найквиста для непрерывных систем. ,
,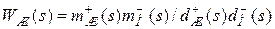 .
. ,
,  передаточной функции
передаточной функции  .
. , также как ранее для непрерывных систем.
, также как ранее для непрерывных систем.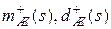 строится асимптотическая желаемая ЛАХ
строится асимптотическая желаемая ЛАХ  по заданным показателям качества
по заданным показателям качества 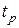 ,
, 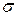 , которая изображается на графике ЛАХ нескорректированной системы
, которая изображается на графике ЛАХ нескорректированной системы  . При этом следует учитывать, что
. При этом следует учитывать, что 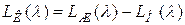 ,
, .
. определяется в результате обратного преобразования
определяется в результате обратного преобразования  .
. дискретной коррекции составляется алгоритм вычисления управляющего сигнала. Для этого передаточная функция записывается в виде:
дискретной коррекции составляется алгоритм вычисления управляющего сигнала. Для этого передаточная функция записывается в виде: .
.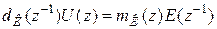 ,
,
 ;
; 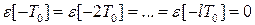 .
. необходимо, чтобы полюса передаточной функции
необходимо, чтобы полюса передаточной функции 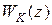 , т.е. корни уравнения
, т.е. корни уравнения  , лежали внутри единичной окружности комплексной плоскости. При этом ошибки вычисления
, лежали внутри единичной окружности комплексной плоскости. При этом ошибки вычисления  умножений и
умножений и  сложений (вычитаний), приводит к запаздыванию управления на время
сложений (вычитаний), приводит к запаздыванию управления на время  , которое не должно превышать период дискретности
, которое не должно превышать период дискретности 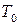 .
. передаточную функцию
передаточную функцию .
. с проведем синтез дискретной коррекции частотным методом с помощью программы составленной в Script-файле:
с проведем синтез дискретной коррекции частотным методом с помощью программы составленной в Script-файле: ,
,  .
. с,
с,  %.
%.
 , вызванного ошибками вычислений, передаточную функцию
, вызванного ошибками вычислений, передаточную функцию  можно записать в виде
можно записать в виде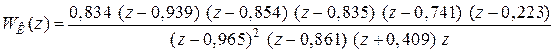 .
. будет работать устойчиво, т.е. ошибки вычисления накапливаться не будут.
будет работать устойчиво, т.е. ошибки вычисления накапливаться не будут.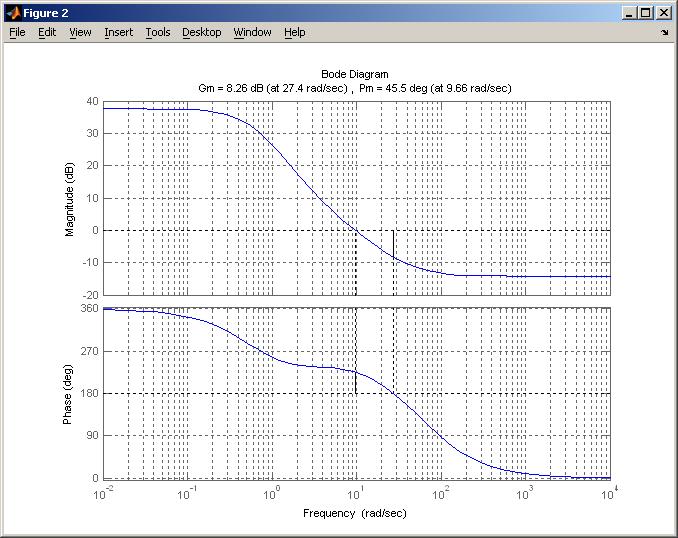

 требуется 10 умножений и 8 сложений (вычитаний). Если согласно [27] принять, что время выполнения операций умножения и сложения соизмеримы и составляет примерно 3мкс, то общее время вычисления составит 54 мкс.
требуется 10 умножений и 8 сложений (вычитаний). Если согласно [27] принять, что время выполнения операций умножения и сложения соизмеримы и составляет примерно 3мкс, то общее время вычисления составит 54 мкс. мкс = 0,001с. Для этого воспользуемся Script-файлом:
мкс = 0,001с. Для этого воспользуемся Script-файлом: с,
с,  %.
%.


