
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение параметров автоколебанийСодержание книги
Поиск на нашем сайте
После синтеза корректирующего устройства необходимо исследовать динамику замкнутой системы при учете нелинейностей функциональных элементов. Наличие нелинейных элементов в системе может привести к потере устойчивости системы или к возникновению незатухающих периодических движений, которые называются автоколебаниями. Тем самым, нелинейности функциональных элементов могут приводить к ухудшению качества переходных процессов и снижению точности системы. Целью исследования условий возникновения автоколебаний и определения их параметров (амплитуды и частоты) является оценка точности системы и при необходимости синтез вспомогательной коррекции для исключения автоколебаний или обеспечения заданной точности.
При учете нелинейного элемента структурную схему системы с последовательной непрерывной коррекцией для нелинейных элементов № 1-3 можно представить в виде рис. 39, для нелинейного элемента № 4 схем Г, Д – рис. 40. Здесь приняты обозначения: При функционировании системы возможны режимы: первый – отработка начальных отклонений системы при отсутствии входного воздействия; второй – отработка входного воздействия при различных начальных отклонениях. Здесь при устойчивом функционировании замкнутой системы, когда переходные процессы ограничены, возможны случаи: в первом режиме автоколебания отсутствуют, при этом они могут возникнуть во втором режиме и наоборот; автоколебания могут отсутствовать или возникать в каждом режиме. Рассмотрим первый режим, полагая в схемах рис. 39, рис.40 сигнал Для определения параметров автоколебаний и исследования их устойчивости можно использовать аналитический или графоаналитический способы, рассмотренные в [2, с.359-367; 4, с.256-259; 9, с.15-21, 19, с.81-86]. Учитывая сложность аналитических вычислений для систем высокого порядка, рассмотрим графо-аналитический способ определения параметров автоколебаний и исследование их устойчивости с использованием критерия Найквиста. С учетом гипотезы существования в замкнутой системе периодических колебаний близких к гармоническим
где Тогда передаточная функция разомкнутой системы, охваченная отрицательной обратной связью для структурных схем рис. 39, рис. 40, имеет вид:
При этом характеристическое уравнение замкнутой системы определяется из уравнения
и с учетом выражения
Для существования гармонических незатухающих колебаний с частотой
или
при Для определения параметров автоколебаний воспользуемся первым уравнением, которое перепишем в виде:
Здесь параметры автоколебаний При наличии автоколебаний для найденной частоты
Здесь в зависимости от того насколько левая часть в неравенстве больше правой настолько возрастает точность гармонической линеаризации нелинейного элемента. Проверку условия фильтра можно проводить по виду ЛАХ
Один из приближенных методов исследования устойчивости найденных периодических решений – метод вариации амплитуды и частоты на основе критерия Найквиста [9, с.18-21; 19, с.82-86]. Из критерия Найквиста для гармонически линеаризованной разомкнутой системы с передаточной функцией В таблице П.2 (Приложение Б) приведены выражения коэффициентов Выражения нелинейных элементов таблицы П.2 удобно представить в зависимости от величины Если характеристика Из таблицы П.3 следует, что для нелинейностей № 1,2 независимо от величины параметра Для построения графиков функций
%Желаемая передаточная функция Wgpas=75.5*tf([1/3.06 1],[1/0.7 1])*tf([1],[1/0.7 1])... *tf([1],[1/45.31 1])*tf([1],[1/45.31 1]); figure(1);nyquist(Wgpas);hold on;% АФЧХ Wgpas(jw) %Нелинейный элемент № 1 a=1:0.1:100; q=1-2/pi*(asin(1./a)+(1./a).^2.*(a.^2-1).^0.5); Wn1=-1./q+i*1e-20*a; % Построение годографа -1/Wнэ(a) plot(Wn1)
Результат построения приведен на рис. 42, из которого следует, что точки пересечения
Рис. 42
При этом АФЧХ В силу приближенности метода гармонической линеаризации даже при выполнении условия фильтра в некоторых случаях автоколебания для найденной частоты Для уточнения параметров автоколебаний необходимо провести моделирования замкнутой системы в соответствии со структурной схемой рис. 39 или рис. 40. Схема моделирования системы с передаточной функцией Wgpas
Рис. 43 Моделирование системы следует провести для одного из значений Отметим, что ценность метода гармонической линеаризации состоит в том, что с его помощью удается сформировать условия на вид АФЧХ
|
|||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.007 с.) |



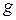 – входной сигнал;
– входной сигнал;  – условный выход системы;
– условный выход системы;  – рассогласование;
– рассогласование;  – нелинейная функция;
– нелинейная функция;  – желаемая передаточная функция разомкнутой системы найденная в подразделе 3.8. На рис. 39 параметры нелинейности
– желаемая передаточная функция разомкнутой системы найденная в подразделе 3.8. На рис. 39 параметры нелинейности 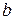 нелинейного элемента № 4 следует увеличить в
нелинейного элемента № 4 следует увеличить в 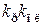 раз.
раз.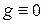 .
. , где
, где  – амплитуда и
– амплитуда и  – частота предполагаемых автоколебаний (параметры автоколебаний), по виду нелинейного элемента заменяем его нелинейную характеристику передаточной функцией
– частота предполагаемых автоколебаний (параметры автоколебаний), по виду нелинейного элемента заменяем его нелинейную характеристику передаточной функцией .
. ,
,  – коэффициенты гармонической линеаризации.
– коэффициенты гармонической линеаризации. .
.
 имеет вид:
имеет вид: .
. имело левые корни и пару комплексно-сопряженных чисто мнимых корней
имело левые корни и пару комплексно-сопряженных чисто мнимых корней  . Полагая
. Полагая  , с учетом выражения
, с учетом выражения  найдем уравнение для определения амплитуды
найдем уравнение для определения амплитуды 
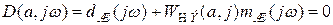
 ,
,  для найденного решения.
для найденного решения.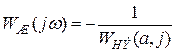 .
. и
и  , построенных на комплексной плоскости при изменении
, построенных на комплексной плоскости при изменении  и
и 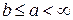 , где
, где  – параметр нелинейного элемента.
– параметр нелинейного элемента.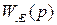 в виде неравенства:
в виде неравенства: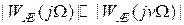 ,
, 
 , которая в соответствии с методикой синтеза в большинстве случаев убывает при
, которая в соответствии с методикой синтеза в большинстве случаев убывает при  .
. Найденные периодические решения, удовлетворяющие условию фильтра, могут быть устойчивыми (т.е. обладают свойством асимптотической орбитальной устойчивости) и неустойчивыми. Если периодическое решение устойчиво, то фазовые траектории стягиваются к предельному циклу, который разделяет фазовую плоскость на две области I и II (рис. 41) с качественно различным характером фазовых траекторий; если периодическое решение неустойчиво, то фазовые траектории удаляются от предельного цикла (в этом случае область II предельного цикла определяет область устойчивости положения равновесия).
Найденные периодические решения, удовлетворяющие условию фильтра, могут быть устойчивыми (т.е. обладают свойством асимптотической орбитальной устойчивости) и неустойчивыми. Если периодическое решение устойчиво, то фазовые траектории стягиваются к предельному циклу, который разделяет фазовую плоскость на две области I и II (рис. 41) с качественно различным характером фазовых траекторий; если периодическое решение неустойчиво, то фазовые траектории удаляются от предельного цикла (в этом случае область II предельного цикла определяет область устойчивости положения равновесия). следует, что для устойчивости автоколебаний необходимо, чтобы годограф
следует, что для устойчивости автоколебаний необходимо, чтобы годограф  пересекал годограф
пересекал годограф  ,
, 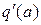 передаточной функции
передаточной функции  для нелинейных элементов № 1-4.
для нелинейных элементов № 1-4. , которая изменяется в пределах
, которая изменяется в пределах  . В таблице П.3 приведены указанные зависимости и графическое изображение характеристик
. В таблице П.3 приведены указанные зависимости и графическое изображение характеристик  с учетом заданных параметров нелинейностей
с учетом заданных параметров нелинейностей 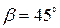 ,
,  .
.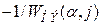 при изменении
при изменении  в некоторой точке при
в некоторой точке при 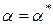 , то значение амплитуды возможных автоколебаний определяется по формуле
, то значение амплитуды возможных автоколебаний определяется по формуле  .
. ; для нелинейности № 3 – полуось
; для нелинейности № 3 – полуось  . Для нелинейности № 4 в таблице П.3 приведена характеристика
. Для нелинейности № 4 в таблице П.3 приведена характеристика 
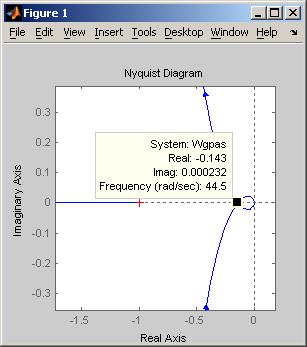
 со значением
со значением  . Поэтому, если увеличить коэффициент усиления передаточной функции
. Поэтому, если увеличить коэффициент усиления передаточной функции  раз, то получим пересечение указанных характеристик. Однако при этом автоколебания не возникают, поскольку характеристика
раз, то получим пересечение указанных характеристик. Однако при этом автоколебания не возникают, поскольку характеристика  при изменении
при изменении  извне вовнутрь, что соответствует неустойчивому предельному циклу. Это означает, что в некоторой области фазовые траектории стягиваются к началу координат, а за пределами данной области уходят в бесконечность. Тем самым замкнутая система устойчивая в большом и неустойчивая в целом.
извне вовнутрь, что соответствует неустойчивому предельному циклу. Это означает, что в некоторой области фазовые траектории стягиваются к началу координат, а за пределами данной области уходят в бесконечность. Тем самым замкнутая система устойчивая в большом и неустойчивая в целом.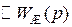 , kne
, kne  представлена на рис. 43, где на вход системы подается короткий исчезающий импульс для возбуждения автоколебаний такой, чтобы переходной процесс
представлена на рис. 43, где на вход системы подается короткий исчезающий импульс для возбуждения автоколебаний такой, чтобы переходной процесс  превысил значение параметр
превысил значение параметр 
 , при котором возникают автоколебания, и при
, при котором возникают автоколебания, и при  для исходной системы. Изменяя амплитуду входного импульса добиться возникновения автоколебаний или убедиться в их отсутствии.
для исходной системы. Изменяя амплитуду входного импульса добиться возникновения автоколебаний или убедиться в их отсутствии.


