
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение лах и лфх разомкнутой системы и Определение запасов устойчивости замкнутой системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Построение ЛАХ и ЛФХ разомкнутой системы можно проводить ручным и машинным способом. Для использования ручного способа построения асимптотической ЛАХ и ЛФХ необходимо, чтобы исходная передаточная функция была представлена в стандартном виде, т.е. в виде произведения типовых звеньев. При необходимости приведение к стандартному виду произвольной передаточной функции можно проводить с помощью функции zpk. Например, для передаточной функции
при выполнении командной строки >> W=tf([3 6 2],[200 10 3 0]),W1=zpk(W)
Transfer function: 3 s^2 + 6 s + 2 ---------------------- 200 s^3 + 10 s^2 + 3 s
Zero/pole/gain: 0.015 (s+1.577) (s+0.4226) -------------------------- s (s^2 + 0.05s + 0.015) исходная передаточная функция представлена в виде Zero/pole/gain, т.е. в виде произведения типовых звеньев, у которых свободные члены отличны от единицы. Для приведения передаточной функции к стандартному виду необходимо свободные члены вынести за скобки. Ручной способ построения асимптотической ЛАХ и ЛФХ по передаточной функции разомкнутой системы проводится в следующей последовательности: · исходная передаточная функция представляется в стандартном виде:
где · определяется значение · определяются сопрягающие частоты · строится асимптотическая ЛАХ: через точку в сопрягающей частоте ЛАХ терпит излом относительно предыдущего участка на далее проводится прямая до следующей сопрягающей частоты, в которой ЛАХ терпит излом аналогично предыдущему; в области высоких частот ЛАХ уходит в бесконечность с наклоном · строится ЛФХ в виде суммы ЛФХ типовых звеньев, входящих в передаточную функцию, при этом в области низких частот ЛФХ начинается со значения При ручном способе построения ЛАХ и ЛФХ следует использовать масштаб: по оси ординат 20 дБ - 40 мм и I град - I мм; по оси частот 1 дек - 100 мм. При построении ЛФХ воспользоваться шаблонами ЛФХ апериодического и колебательного звена с заданным коэффициентом затухания, построенных с помощью таблиц [1] и вырезанных из ватмана. При машинном способе построения с использованием системы MATLAB строится точная ЛАХ, на которую следует нанести график асимптотической ЛАХ, которая в дальнейшем используется для синтеза последовательного корректирующего устройства. Рассмотрим машинный способ построение ЛАХ и ЛФХ с помощью системы MATLAB для рассмотренной выше передаточной функции разомкнутой системы схемы А:
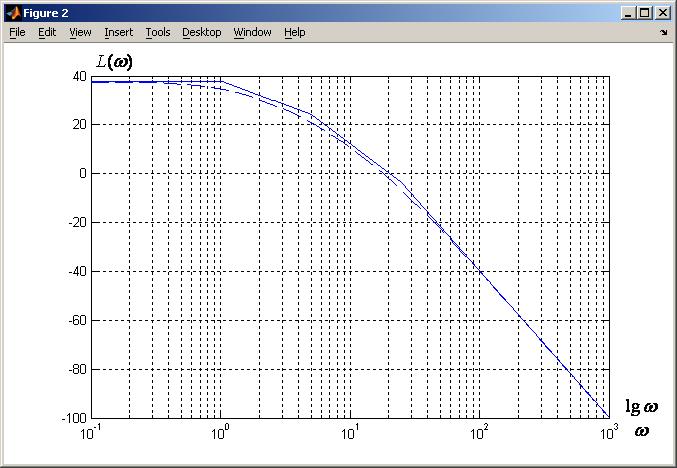
для принятых параметров Воспользуемся вспомогательной программой, составленной в Script-файле: % передаточная функция разомкнутой системы Wpas=75.5*tf([0.4 1],[0.04 1])*tf([1],[0.2 1])*tf([1],[0.96 1])*tf([1],[0.38 1]); % сопрягающие частоты omega=[0.1 1/0.96 1/0.4 1/0.38 1/0.2 1/0.04 1/0.001]; % построение ЛАХ и ЛФХ, запасов устойчивости по амплитуде и фазе margin(Wpas); grid on; figure % построение асимптотическая ЛАХ в заданной области частот по передаточной функции L1=20*log10(75.5);L2=20*log10(75.5);L3=L2-20*log10(0.96/0.4); L4=L3;L5=L4-20*log10(0.38/0.2);L6=L5-40*log10(0.2/0.04);L7=L6-60*log10(0.04/0.001); L=[L1 L2 L3 L4 L5 L6 L7]; semilogx(omega,L); grid on; hold on % точная ЛАХ для сравнения [Lg,f,w]=bode(Wpas,{0.1,1000});Lg1=20*log10(squeeze(Lg)); semilogx(w,Lg1,'--') Приведенный текст программы можно скопировать и вставить в рабочее поле m-file, которое открывается при нажатии левой верхней кнопки в среде MATLAB. Затем выполнить программу нажатием кнопки со стрелкой Если программу оформить в виде m-файла с помощью оператора function, то переменные будут локальными в пределах данного m-файла. В результате выполнения получим графики представленные на рис. 17, рис.18.
Рис. 17
Рис. 18
Согласно критерию Найквиста для устойчивости замкнутой отрицательной единичной обратной связью физически реализуемой разомкнутой системы с передаточной функцией Подсчет охватов удобно проводить с помощью правила Цыпкина, согласно которому сумма охватов точки
где характеристическое уравнение замкнутой системы Логарифмический аналог критерия Найквиста устанавливается с учетом связи АФЧХ и ЛАХ и ЛФХ передаточной функции Пересечение ЛФХ линий На рис. 17 представлены точные ЛАХ и ЛФХ с указанными значениями запасов устойчивости по амплитуде: На рис. 18 представлена асимптотическая ЛАХ (и точная ЛАХ для сравнения), которая может быть использована в дальнейшем для синтеза последовательной коррекции. Графики рис. 17, рис. 18 следует представлять в наибольшем масштабе (растянуть и отредактировать график аналогично предыдущему) и вставлять в текст документа Word, выбирая параметры данной страницы "альбомная". В соответствии с логарифмическим аналогом критерия Найквиста замкнутая система неустойчива. Для устойчивой замкнутой системы значения Критический коэффициент усиления разомкнутой системы
при этом Значение критической частоты Для минимально-фазовых передаточных функций Для рис. 14 при уточненном значении
>> Kpas=75.5;Kkp=Kpas/abs(freqresp(Wpas,[12.6518]))
В результате получим значение Kkp =35.3756 равное значению, найденному с помощью метода D – разбиения. Для проверки правильности полученного результата можно также построить годографы движения корней характеристического уравнения замкнутой системы при изменении коэффициента усиления разомкнутой системы >> WKpas=Wpas/Kpas; rlocus(WKpas);
Результат вычислений представлен на рис. 19. С помощью левой клавиши мыши отметить точку пересечения одной из ветвей годографа с мнимой осью комплексной плоскости корней и не отпуская клавишу подвигать точку в левую и правую сторону. При этом в открывшемся окне будут указаны значения коэффициента усиления Таким образом, при Вычислить корни характеристического уравнения замкнутой системы при выбранном коэффициенте усиления можно с помощью командной строки >> Kkp=35.3756; p=esort(tzero(1+Kkp*Wpas/Kpas))
Рис. 19
в результате выполнения которой получим p = -0.0000 +12.6518i -0.0000 -12.6518i -2.4977 -31.1754
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1910; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.147.12 (0.007 с.) |


 ,
, – коэффициент усиления разомкнутой системы;
– коэффициент усиления разомкнутой системы;  ,
,  ; порядок полинома числителя
; порядок полинома числителя  не превышает порядка знаменателя
не превышает порядка знаменателя  , что соответствует физически реализуемым системам;
, что соответствует физически реализуемым системам; ;
; , вычисляются
, вычисляются  ;
; дБ/дек до первой слева сопрягающей частоты, где
дБ/дек до первой слева сопрягающей частоты, где 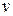 – число интегрирующих звеньев в передаточной функции (если
– число интегрирующих звеньев в передаточной функции (если  , то прямая проводится параллельно оси частот; если вместо интегрирующих звеньев присутствуют
, то прямая проводится параллельно оси частот; если вместо интегрирующих звеньев присутствуют  дифференцирующих звеньев, то следует принять
дифференцирующих звеньев, то следует принять  и наклон асимптоты будет положительным);
и наклон асимптоты будет положительным); дБ/дек или
дБ/дек или  дБ/дек. Если сопрягающей частоте соответствует звено первого порядка, то излом составляет
дБ/дек. Если сопрягающей частоте соответствует звено первого порядка, то излом составляет 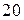 дБ/дек, для звена второго порядка (с комплексно-сопряженными корнями) соответственно
дБ/дек, для звена второго порядка (с комплексно-сопряженными корнями) соответственно  дБ/дек. Знак "+" соответствует звеньям, расположенных в числителе, а знак "–" в знаменателе передаточной функции;
дБ/дек. Знак "+" соответствует звеньям, расположенных в числителе, а знак "–" в знаменателе передаточной функции;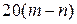 дБ/дек, где
дБ/дек, где  рад, а в области высоких частот ЛФХ стремится к значению
рад, а в области высоких частот ЛФХ стремится к значению  рад.
рад. ,
, ;
;  ;
; 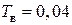 ;
; 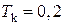 ;
;  ;
;  .
. (Run) на панели инструментов m-file. При этом вычисленные переменные в Script-файле являются глобальными и доступны в любом другом Script-файле, а также в среде MATLAB.
(Run) на панели инструментов m-file. При этом вычисленные переменные в Script-файле являются глобальными и доступны в любом другом Script-файле, а также в среде MATLAB.
 , необходимо и достаточно, чтобы АФЧХ
, необходимо и достаточно, чтобы АФЧХ 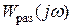 охватывала точку
охватывала точку  с учетом знака в сумме
с учетом знака в сумме  раз, где
раз, где  число правых корней характеристического уравнения разомкнутой системы
число правых корней характеристического уравнения разомкнутой системы  . При этом следует считать, что при наличии
. При этом следует считать, что при наличии  при
при 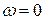 дополняется дугой бесконечно большого радиуса с раствором угла
дополняется дугой бесконечно большого радиуса с раствором угла  против часовой стрелки (по часовой стрелке – отрицательный охват). Принятые знаки поворота радиус-вектора объясняются тем, что углу
против часовой стрелки (по часовой стрелке – отрицательный охват). Принятые знаки поворота радиус-вектора объясняются тем, что углу  , отложенному от вещественной положительной полуоси, в первом квадранте соответствует
, отложенному от вещественной положительной полуоси, в первом квадранте соответствует  и, следовательно,
и, следовательно,  , а в четвертом квадранте
, а в четвертом квадранте  и, следовательно,
и, следовательно,  .
. в соответствии с рис. 19, на котором показаны возможные случаи переходов вещественной полуоси
в соответствии с рис. 19, на котором показаны возможные случаи переходов вещественной полуоси  При прохождении АФЧХ
При прохождении АФЧХ  , которому соответствует уравнение
, которому соответствует уравнение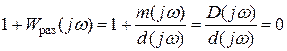 ,
, имеет пару мнимых корней
имеет пару мнимых корней  при некотором значении
при некотором значении  .
.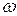 , соответствующих положительным значениям
, соответствующих положительным значениям  , сумма переходов ЛФХ через линии
, сумма переходов ЛФХ через линии  с учетом знаков (положительный – снизу вверх, отрицательными – сверху вниз и т.д.) равнялась
с учетом знаков (положительный – снизу вверх, отрицательными – сверху вниз и т.д.) равнялась  плоскости АФЧХ. В большинстве случаев, в том числе для рассматриваемых схем САУ, ЛФХпересекает только одну линию
плоскости АФЧХ. В большинстве случаев, в том числе для рассматриваемых схем САУ, ЛФХпересекает только одну линию  .
. (при частоте 12,7 рад/с) и фазе
(при частоте 12,7 рад/с) и фазе  град (при частоте 18 рад/с).
град (при частоте 18 рад/с). должны быть положительными.
должны быть положительными. , при котором замкнутая система с отрицательной единичной обратной связью находится на границе устойчивости, определяется согласно критерию Найквиста из условия
, при котором замкнутая система с отрицательной единичной обратной связью находится на границе устойчивости, определяется согласно критерию Найквиста из условия ,
,
 .
. можно найти с помощью ЛФХ из условия
можно найти с помощью ЛФХ из условия  град, при этом для критического коэффициент усиления
град, при этом для критического коэффициент усиления  , что может быть использовано при графическом определении
, что может быть использовано при графическом определении  соответствует границе колебательной устойчивости.
соответствует границе колебательной устойчивости. 12,6518 рад/с вычисление
12,6518 рад/с вычисление  с помощью командной строки
с помощью командной строки в замкнутой системе все корни устойчивые из них одна пара комплексно-сопряженных корней
в замкнутой системе все корни устойчивые из них одна пара комплексно-сопряженных корней  ; при
; при  ,
,  пара комплексно-сопряженных корней становится неустойчивой:
пара комплексно-сопряженных корней становится неустойчивой:  .
.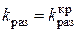 замкнутая система находится на границе колебательной устойчивости и при
замкнутая система находится на границе колебательной устойчивости и при 



