
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неинерциальные системы отсчета (НИСО). Уравнение движения материальной точки в НИСО.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Различают В механике НИСО: 1). Ускорение тел вызывается силами, но эти силы не обязательно обусловлены действием тел друг друга. 2). в НИСО действуют: Абсолютное движение – движение относительно сист К. Относительное движение – движение тела относительно движущейся СО. Переносное движение – движение, кот покоится в системе
Силы инерции. Сила инерции – векторная величина, численно равная произведению мат точки на ее ускорение (ускорение НИСО) и направленная противоположно ускорению. 1). тело покоится во вращающейся с пост угл скоростью в НИСО:
3). Тело движется во вращающейся с пост Си́ла Кориоли́са — одна из сил инерции, существующая в неинерциальной системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения. Названа по имени французского учёного Гюстава Гаспара Кориолиса, впервые её описавшего. Ускорение Кориолиса было получено Кориолисом в 1833 году, Гауссом в 1803 году и Эйлеромв 1765 году. Причина появления силы Кориолиса — в кориолисовом (поворотном) ускорении. В инерциальных системах отсчёта действует закон инерции, то есть, каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось, требуется придавать телу ускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса. Для того, чтобы тело двигалось с кориолисовым ускорением, необходимо приложение силы к телу, равной Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки — то вправо. Сила Кориолиса в природе Сила Кориолиса, вызванная вращением Земли, может быть замечена при наблюдении за движением маятника Фуко[1]. Кроме того, сила Кориолиса проявляется и в глобальных масштабах. В северном полушарии сила Кориолиса направлена вправо от движения, поэтому правые берега рек в Северном полушарии более крутые — их подмывает вода под действием этой силы[2] (см. Закон Бэра). В Южном полушарии всё происходит наоборот. Сила Кориолиса ответственна также и за вращение циклонов и антициклонов[3] (см. геострофический ветер): в Северном полушарии вращение воздушных масс происходит в циклонах против часовой стрелки, а в антициклонах — по стрелке; в Южном — наоборот: по часовой стрелке в циклонах и против — в антициклонах. Отклонение ветров (пассатов) при циркуляции атмосферы — также проявление силы Кориолиса. Если бы рельсы были бы идеальными, то при движении железнодорожных составов с севера на юг и с юга на север, под воздействием силы Кориолиса один рельс изнашивался бы сильнее, чем второй. В северном полушарии больше изнашивается правый, а в южном левый[4]. Силу Кориолиса необходимо учитывать при рассмотрении планетарных движений воды в океане. Она является причиной возникновения гироскопических волн[5]. При идеальных условиях сила Кориолиса определяет направление закручивания воды например, при сливе в раковине. Однако идеальные условия трудно достижимы. Поэтому феномен «обратного закручивания воды при стоке» является скорее околонаучной шуткой. 11) Импульс. Вывод закона сохранения импульса из второго закона динамики. Центр масс системы материальных точек. Импульсом, или количеством движения материальной точки называется векторная величина, равная произведению массы материальной точки m на скорость ее движения v. – для материальной точки; – для системы материальных точек (через импульсы этих точек); – для системы материальных точек (через движение центра масс). Центром масс системы называется точка С, радиус-вектор rC которой равен ,где Уравнение движения центра масс:
Смысл уравнения таков: произведение массы системы на ускорение центра масс равно геометрической сумме внешних сил, действующих на тела системы. Как видим, закон движения центра масс напоминает второй закон Ньютона. Если внешние силы на систему не действуют или сумма внешних сил равна нулю, то ускорение центра масс равно нулю, а скорость его неизменна во времени по модулю и наплавлению, т.е. в этом случае центр масс движется равномерно и прямолинейно. В частности, это означает, что если система замкнута и центр масс ее неподвижен, то внутренние силы системы не в состоянии привести центр масс в движение. На этом принципе основано движение ракет: чтобы ракету привести в движение, необходимо выбросить выхлопные газы и пыль, образующиеся при сгорании топлива, в обратном направлении. Закон Сохранения Импульса Для вывода закона сохранения импульса рассмотрим некоторые понятия. Совокуп ность материальных точек (тел), рассмат риваемых как единое целое, называется механической системой. Силы взаимодей ствия между материальными точками ме ханической системы называются внутрен ними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной). Если мы имеем механиче скую систему, состоящую из многих тел, то, согласно третьему закону Ньютона, силы, действующие между этими телами, будут равны и противоположно направле ны, т. е. геометрическая сумма внутренних сил равна нулю. Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны т 1, m 2,..., тn и v 1, v 2,..., v n. Пусть F '1, F '2,..., F 'n — равнодействующие внутренних сил, действующих на каждое из этих тел, a f 1, f 2,..., F n — равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из n тел механической системы: d/dt(m1v1)= F '1+ F 1, d/dt(m2v2)= F' 2+ F 2, d/dt(mn v n)= F 'n+ F n. Складывая почленно эти уравнения, получим d/dt (m1 v 1+m2 v 2+... + mn v n) = F '1+ F '2+...+ F ' n + F 1+ F 2+...+ F n. Но так как геометрическая сумма внутрен них сил механической системы по третьему закону Ньютона равна нулю, то d/dt(m1v1+m2v2 +... + mnvn)= F 1 + F 2+...+ F n, или dp/dt= F 1+ F 2+...+ F n, (9.1) где импульс системы. Таким образом, производная по времени от им пульса механической системы равна гео метрической сумме внешних сил, действующих на систему.
В случае отсутствия внешних сил (рассматриваем замкнутую систему)
Это выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени. Закон сохранения импульса справед лив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выполняется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). Этот закон носит универсальный характер, т. е. закон со хранения импульса — фундаментальный закон природы. 12. Физические основы космических полетов: законы движения тел переменной массы.
Пусть в результате этого процесса за время dt скорость ракеты изменится на величину d υ, а ее масса m уменьшится на dm. Тогда изменение импульса системы "ракета, топливо" можно рассчитать с помощью соотношения: d p = ((m - dm)·(υ + d υ) + dm· u) - m· υ, Согласно закону преобразования скоростей, запишем следующее векторное равенство: u = υ т + υ, Из уравнений (14), (15) получим формулу для расчета изменения импульса системы за время dt. d p = m·d υ + υ т·dm. Согласно второму закону Ньютона скорость изменения импульса равна равнодействующей внешних сил F, действующих на систему. Проведя разделение переменных, преобразуем уравнение (16) к виду: d υ = - υ т·dm/m. Проведя интегрирование (17) по скорости от 0 до υ и массе от m0 до m, получим формулу Циолковского (18), позволяющую рассчитать скорость ракеты в зависимости от соотношения масс ракеты с топливом в начальный m0 и текущий m моменты времени и скорости истечения продуктов сгорания топлива относительно ракеты: υ = υт·ln (m0/m). Формулу (18) можно привести к виду, позволяющему определить, каково должно быть отношение массы ракеты с топливом к массе корпуса ракеты mкдля достижения ракетой заданной скорости υ, например, первой космической.
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 955; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |

 ,
,  ,
,  . В СО связанные с Землей, на каждое тело действует
. В СО связанные с Землей, на каждое тело действует  – весом называют силу, с кот любое тело в поле сил тяжести, созданным небесным объектом, действует на опору или подвес, кот препятствует свободному падению тел. Отметим, что сила тяж и веса приложены к разным объектам: вес – к опоре,
– весом называют силу, с кот любое тело в поле сил тяжести, созданным небесным объектом, действует на опору или подвес, кот препятствует свободному падению тел. Отметим, что сила тяж и веса приложены к разным объектам: вес – к опоре,  – к телу. Эти силы имеют различную физическую природу: вес – упругую природу (электромагнитная), а
– к телу. Эти силы имеют различную физическую природу: вес – упругую природу (электромагнитная), а  тела относительно Земли отличается от
тела относительно Земли отличается от  по 2 закону Ньютона:
по 2 закону Ньютона:  . Тогда по определению вес тела
. Тогда по определению вес тела  . При свободном падении тела вместе с опорой (подвесом) вес
. При свободном падении тела вместе с опорой (подвесом) вес  равен нулю, т.к.
равен нулю, т.к.  . Невесомость – состояние тела, при кот оно движется только под действием силы тяжести. Введение сил инерции позволяет для ИСО ввести уравнение, подобное 2-ому з Ньютона, внешний вид которого сохраняется за счет введения сил инерции.
. Невесомость – состояние тела, при кот оно движется только под действием силы тяжести. Введение сил инерции позволяет для ИСО ввести уравнение, подобное 2-ому з Ньютона, внешний вид которого сохраняется за счет введения сил инерции.  ,
,  (уравнение движения в НИСО),
(уравнение движения в НИСО),  - ускорение в НИСО.
- ускорение в НИСО. , кот присутствуют из-за ускоренного движения сист
, кот присутствуют из-за ускоренного движения сист  относительно K. 3). Все силы инерции, подробно силам тяготения, пропорциональны массе тел.
относительно K. 3). Все силы инерции, подробно силам тяготения, пропорциональны массе тел. , кот движ относительно K.
, кот движ относительно K. ,
,  - закон преобразования скорости при переходе от сит К к сист
- закон преобразования скорости при переходе от сит К к сист 
 ,
,  – ускорение в сист К,
– ускорение в сист К,  - ускорение в НИСО,
- ускорение в НИСО, 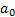 – переносное ускорение, ускорение
– переносное ускорение, ускорение  – геометрическая сумма всех сил, действующих на данное тело со стороныдругих тел,
– геометрическая сумма всех сил, действующих на данное тело со стороныдругих тел,  – сумма сил инерции, действующих на тело.
– сумма сил инерции, действующих на тело. ,
,  – сила натяжения нити,
– сила натяжения нити,  – равнодействующая силы тяжести и силы натяжения нити.
– равнодействующая силы тяжести и силы натяжения нити. 2). В СО, вращающейся с постоянной
2). В СО, вращающейся с постоянной  , на покоящееся в ней тело действует центробежная сила инерции
, на покоящееся в ней тело действует центробежная сила инерции  :
:  . Переносное ускорение при этом:
. Переносное ускорение при этом:  .
. относительно неподвижной ИСО, то переносное ускорение
относительно неподвижной ИСО, то переносное ускорение  . Действуют 3 силы: 1. поступательная сила инерции
. Действуют 3 силы: 1. поступательная сила инерции  . Возникает при поступательном движении НИСО. 2. Центробежная сила инерции
. Возникает при поступательном движении НИСО. 2. Центробежная сила инерции  .Действует во вращающихся СО и на движущиеся, и на неподвижные тела, удаленные от оси вращения на конечное расстояние r. 3. кориолисова сила инерции
.Действует во вращающихся СО и на движущиеся, и на неподвижные тела, удаленные от оси вращения на конечное расстояние r. 3. кориолисова сила инерции  . Действует во вращающейся системе координат только на движущиеся с относительной скоростью
. Действует во вращающейся системе координат только на движущиеся с относительной скоростью  тела. Когда скорость эт движения =0, эта сила исчезает. Она зависит от угловой скорости вращения и относительной скорости вращения. Т.о.
тела. Когда скорость эт движения =0, эта сила исчезает. Она зависит от угловой скорости вращения и относительной скорости вращения. Т.о.  ,
,  – сумма сил, действующих на тело со стороны других тел.
– сумма сил, действующих на тело со стороны других тел. , где
, где  — кориолисово ускорение. Соответственно, тело действует по третьему закону Ньютона с силой противоположной направленности.
— кориолисово ускорение. Соответственно, тело действует по третьему закону Ньютона с силой противоположной направленности.  Сила, которая действует со стороны тела, и будет называться силой Кориолиса. Не следует путать Кориолисову силу с другой силой инерции — центробежной силой, которая направлена по радиусу вращающейся окружности.
Сила, которая действует со стороны тела, и будет называться силой Кориолиса. Не следует путать Кориолисову силу с другой силой инерции — центробежной силой, которая направлена по радиусу вращающейся окружности.


 .
.


