
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическая теория теплоемкости идеального газа.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Обьект - ИГ Теплоемкостью тела С называется отношение бесконечно ма юго количества тепла бQ, полученного телом, к соответствующему приращению dT его температуры:
32. Адиабатный процесс.
Адиабатный процесс — это процесс, происходящий без теплообмена системы с окружающей средой, т.е. Q = 0. Первый закон термодинамики имеет вид:
Это значит, что при адиабатном процессе система может выполнять работу над внешними телами только за счет убыли своей внутренней энергии. Если А > 0, то Δ U = - A < 0, т.е. U 2 < U 1, а так как Как известно, газ совершает положительную работу, если Δ V > 0. Таким образом, при адиабатном расширении газ совершает работу и сам охлаждается. Наоборот, при адиабатном сжатии А < 0 над газом совершается работа и газ нагревается. При адиабатном процессе давление и объем связаны между собой уравнением
где γ > 1 — показатель адиабаты (или коэффициент Пуассона). Это уравнение называется уравнением адиабаты или уравнением Пуассона. Адиабатное изменение состояния газа можно выразить графически. График этого процесса называют адиабатой. При одних и тех же начальных условиях (p 0, V 0) при адиабатном расширении давление газа уменьшается быстрее, чем при изотермическом (рис. 1), так как падение давления вызвано не только увеличением объема (как при изотермическом расширении), но и понижением температуры. Поэтому адиабата идет ниже изотермы и газ при адиабатном расширении совершает меньшую работу, чем при изотермическом расширении.
Рис. 1 При быстром сжатии (расширении) теплообмен произойти не успевает и процессы можно рассматривать как адиабатные (неравновесные). Поэтому любой газ при быстром сжатии нагревается (например, нагревание насоса при накачивании велосипедной шины). При сильном и быстром сжатии воздуха температура может повыситься настолько, что при наличии в воздухе паров бензина они воспламеняются. Это используется в дизельных двигателях для зажигания горючей смеси. Этим объясняется необходимость специального охлаждения мощных компрессоров. Охлаждение воздуха при адиабатном расширении вызывает образование облаков. Политропические процессы. Политропные процессы Политропные процессы. Уравнения политропных процессов и их энергетические характеристики. Анализ частных случаев политропных процессов: изобарный, изотермический, адиабатный и изохорный. Обобщенная рабочая диаграмма политропных процессов. Зависимость теплоемкости от показателя политропы. Численное определение показателя политропы.
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 4497; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.154.204 (0.012 с.) |

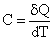
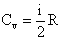
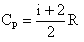
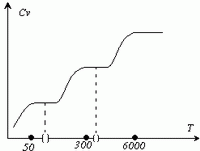
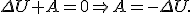
 , то T 2 < T 1.
, то T 2 < T 1.

 Понятие “политропные процессы” представляет собой обобщающую модель всего многообразия термодинамических процессов в идеальных газах, протекающих при постоянном значении теплоемкости. Идентификация процессов осуществляется по показателю политропы n, который определяет связь между параметрами состояния в виде уравнений политропных процессов Pvn= const; Tvn-1= const; TnP1-n= const.
Понятие “политропные процессы” представляет собой обобщающую модель всего многообразия термодинамических процессов в идеальных газах, протекающих при постоянном значении теплоемкости. Идентификация процессов осуществляется по показателю политропы n, который определяет связь между параметрами состояния в виде уравнений политропных процессов Pvn= const; Tvn-1= const; TnP1-n= const.


