Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплоемкость (удельная, молярная). Уравнение Майера.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теплоемкость тела показывает, какое количество теплоты необходимо для увеличения температуры тела на 1 градус. Зависит от материала вещества и от массы тела. Удельная теплоемкость Молярная теплоемкость Удельная и молярные теплоемкости идеального газа зависят не только от химического состава газа, но и от процесса, с помощью которого происходит изменение температуры.
Изохорный процесс – при постоянном объеме, значит, работа не совершается. Для одноатомного идеального газа
Удельная теплоемкость в этом процессе
Молярная теплоемкость
2.Изобарный процесс – процесс при постоянном давлении.
Удельная теплоемкость для изобарного процесса
Молярная теплоемкость для изобарного процесса
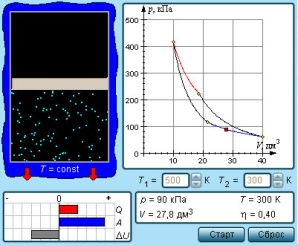
3.Изотермический процесс – это процесс при постоянной температуре.
4.Адиабатный процесс – это процесс при отсутствии теплопередачи с системой. Для реализации такого процесса необходимо изолировать систему от окружающей среды, или процесс должен проходить быстро, не успевая приходить в тепловое равновесие с окружающей средой. Первый закон термодинамики для адиабатного процесса: При адиабатном расширении температура понижается. При адиабатном сжатии температура газа повышается. Уравнение Майера. Найдем связь между Ср и Сv идеального газа. Используя формулы запишем первое начало термодинамики в виде или Ср = Сv + R. (3.16) Формулу (3.16) называют уравнением Майера. Вывод: при изобарическом нагревании газа к нему подводится больше теплоты, чем при изохорическом. Практически изобарический процесс можно осуществить, например, при нагревании или охлаждении газа в цилиндре с подвижным поршнем, на который действует постоянная сила давления. Работу при изобарическом расширении идеального газа можно найти по формуле
или
Если при изменении температуры Ср не изменяется, то теплоту, сообщенную газу в изобарическом процессе, можно найти по формуле
P-V диаграмма изобарического процесса приведена на рис. 3.4, где площадь прямоугольника (заштрихованная часть рисунка) численно равна работе газа в этом процессе. Циклические процессы. Цикл Карно. КПД цикла Карно. Цикл Карно Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1–2) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T1. Газ изотермически расширяется, совершая работу A12, при этом к газу подводится некоторое количество теплоты Q1 = A12. Далее на адиабатическом участке (2–3) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A23 > 0. Температура газа при адиабатическом расширении падает до значения T2. На следующем изотермическом участке (3–4) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре T2 < T1. Происходит процесс изотермического сжатия. Газ совершает работу A34 < 0 и отдает тепло Q2 < 0, равное произведенной работе A34. Внутренняя энергия газа не изменяется. Наконец, на последнем участке адиабатического сжатия газ вновь помещается в адиабатическую оболочку. При сжатии температура газа повышается до значения T1, газ совершает работу A41 < 0. Полная работа A, совершаемая газом за цикл, равна сумме работ на отдельных участках: A = A12 + A23 + A34 + A41 На диаграмме (p, V) эта работа равна площади цикла. Процессы на всех участках цикла Карно предполагаются квазистатическими. В частности, оба изотермических участка (1–2 и 3–4) проводятся при бесконечно малой разности температур между рабочим телом (газом) и тепловым резервуаром (нагревателем или холодильником).Как следует из первого закона термодинамики, работа газа при адиабатическом расширении (или сжатии) равна убыли ΔU его внутренней энергии. Для одного моля газа A = –ΔU = –CV (T2 – T1), где T1 и T2 – начальная и конечная температуры газа. Отсюда следует, что работы, совершенные газом на двух адиабатических участках цикла Карно, одинаковы по модулю и противоположны по знакам A23 = –A41 По определению, коэффициент полезного действия η цикла Карно есть
1.1. КПД цикла С. Карно выразил коэффициент полезного действия цикла через температуры нагревателя T1 и холодильника T2:
Цикл Карно замечателен тем, что на всех его участках отсутствует соприкосновение тел с различными температурами. Любое состояние рабочего тела (газа) на цикле является квазиравновесным, т. е. бесконечно близким к состоянию теплового равновесия с при конечной разности температур рабочего тела и окружающей среды (термостатов), когда тепло может передаваться без совершения работы. Поэтому цикл Карно – наиболее эффективный круговой процесс из всех возможных при заданных температурах нагревателя и холодильника: ηКарно = ηmax
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.78.12 (0.006 с.) |

 показывает, какое количество теплоты необходимо для нагревания 1 килограмма вещества на 1 градус.
показывает, какое количество теплоты необходимо для нагревания 1 килограмма вещества на 1 градус.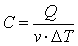 показывает, какое количество теплоты необходимо для нагрева 1 моля вещества на 1 градус.
показывает, какое количество теплоты необходимо для нагрева 1 моля вещества на 1 градус.



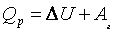

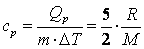

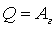 так как
так как 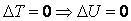
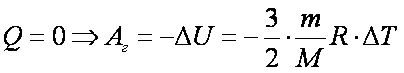
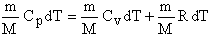
 (3.17)
(3.17) (3.18)
(3.18) (3.19)
(3.19)