
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплоемкость, энтальпия и энтропияСодержание книги
Поиск на нашем сайте
Теплоемкость и ее виды. Удельной теплоемкостью с называют количество теплоты q, которое требуется для изменения температуры единицы количества вещества на один градус: Различают массовую с, объемную с' и мольную
где νо, ρо, μ – удельный объем, плотность и молекулярная масса газа при нормальных условиях (ρо = 1,013 · 105 Па, То = 273 К). Теплоемкость зависит от физической природы рабочего тела, температуры, термодинамического процесса. В технической термодинамике наиболее часто используют изобарную теплоемкость ср (при р = const) и изохорную сν (при ν = const). Связь между этими теплоемкостями определяется соотношением Майера для идеального газа: ср - сν = R, (1.16) где R – газовая постоянная, Дж/кг · К. Зависимостью теплоемкости от температуры часто пренебрегают, и тогда количество теплоты в изобарном и изохорном процессах находится из выражений Qp = Мср (Т2 – Т1) или qр = ср (Т2 – Т1); (1.17) Qν = Мсν (Т2 – Т1) или qν = сν (Т2 – Т1). Из выражения первого закона термодинамики (1.13) и соотношения (1.14) можно получить соотношения для определения изменения внутренней энергии Δu и энтальпии Δh, справедливые для всех термодинамических процессов: dqν = du; du = cνdT; Δu = u2 – u1 = cν (Т2 – Т1); (1.18) dqр = du + рdν = dh; dh = cpdT; Δh = h2 – h1 = cp (Т2 – Т1). Поскольку теплоемкость изменяется с температурой, в зависимости от интервала температур различают истинную с и среднюю сср теплоемкости. Истинная теплоемкость Энтальпия. Вводится расчетным путем: полное – H = U + pV или удельное значение h = u + pν, энтальпия представляет некоторую энергию, равную сумме внутренней энергии и произведения давления на объем. Единицей измерения энтальпии Н является джоуль (Дж) или h, Дж/кг. Энтальпия является функцией состояния. Так как в изобарном процессе dH = dQ, то можно сказать, что энтальпия – это количество теплоты, подведенное в изобарном процессе.
Энтропия. Единицей измерения энтропии S является Дж/К и удельной s – Дж/ кг·К. Эта функция состояния вводится расчетным путем и имеет полный дифференциал
Если представить термодинамический процесс в T-s диаграмме, то площадь под кривой процесса характеризует количество подведенной или отведенной теплоты. Энтропию нельзя измерить, но по физическому смыслу она является мерой температурной ценности теплоты, ее способности превращения в работу. Можно сказать также, что энтропия характеризует потерю работы вследствие необратимости реальных процессов (при этом энтропия возрастает). Обычно при расчете термодинамических процессов определяют не абсолютные значения u, h, s, а изменение в процессе Δu, Δh, Δs.
Первый закон термодинамики для потока рабочего тела В потоке рабочего тела происходит изменение кинетической энергии рабочего тела
или
Теплота, подведенная к потоку рабочего тела, идет на увеличение его энтальпии и кинетической энергии. Так как по первому закону
то
Изменение кинетической энергии потока называют его технической работой, т. е. кинетическая энергия потока рабочего тела равна технической (полезной) работе Пример. В тепловом двигателе (паротурбинная установка) поток пара адиабатно расширяется на лопатках турбины (dq = 0):
Второй закон термодинамики Второй закон термодинамики качественной устанавливает направление перехода теплоты, а также ту ее часть, которую можно перевести в работу в тепловом двигателе. С. Карно (1824 г.) указал на возможность превращения теплоты в полезную работу в двигателях при наличии двух источников теплоты, т. е. необходимым условием для получения работы в тепловом двигателе является разность температур. Циклы, в которых теплота превращается в работу, называются прямыми, или циклами тепловых двигателей. На рис. 1.3 и 1.4 изображены прямой цикл в p-v диаграмме и схема теплового двигателя. Рабочее тело 1 (рис. 1.4) в тепловом двигателе 3 получает из горячего источника 2 с температурой Т1 на участке 1-2 цикла (рис. 1.3) теплоту q1 (подвод теплоты) и совершает работу l1 (площадь 1-а-2-3-4-1). Чтобы процесс непрерывно повторялся, в тепловом двигателе нужно возвратить рабочее тело в начальное состояние 1 путем затраты работы l2 в процессе 2-в-1 (площадь 2-в-1-4-3-2) и отвода теплоты q2 в холодный источник 4 с температурой Т2. В тепловом двигателе часть теплоты (q1 – q2) превращена в работу.
Рис. 1.3. Изображение замкнутого термодинамического процесса (цикла) в р, v – диаграмме Эффективность прямых обратимых циклов оценивают термическим КПД. Термический КПД – это отношение работы цикла ко всей подведенной теплоте.
Термический КПД цикла Карно
Из формулы видно, что Термический КПД цикла Карно имеет максимальное значение, он является эталоном при оценке совершенства любых циклов тепловых двигателей.
Рис. 1.4. Схема теплового двигателя
Диаграммы водяного пара В современной теплоэнергетике водяной пар является основным рабочим телом. Термодинамические таблицы водяного пара могут дать лишь дискретные значения искомых величин. Для изображения процессов водяного пара на практике часто используют диаграммы. Диаграмма T-s водяного пара (рис. 1.5) представляет собой график, построенный в координатах температура-энтропия, на котором нанесены следующие линии: изобары нагрева воды аоа', парообразования а´а´´ и перегрева пара а´´а, верхняя (х = 1) и нижняя (х = 0) пограничные кривые, линии постоянной сухости (х = const). Между пограничными кривыми расположена область влажного пара с различными степенями сухости. Части диаграммы, находящиеся правее х = 1 и левее х = 0, являются соответственно областями перегретого пара и воды. Т-s диаграмма позволяет наглядно оценить изменение температуры водяного пара и теплоту пара в различных процессах. Недостатком использования Т-s диаграммы является необходимость измерения площадей.
Рис. 1.5. Т-s – диаграмма водяного пара Диаграмма h-s водяного пара (рис. 1.6) строится по значениям энтальпии и энтропии на обеих пограничных кривых области насыщения. Указанные данные определяются по таблицам термодинамических свойств воды и водяного пара. Начальной точкой для отсчета энтальпии и энтропии является тройная точка. Изобары-изотермы области насыщения представляют собой наклонные прямые линии p = const. При увеличении давления растет температура насыщения и изобары идут более круто. Крутизна изобар-изотерм возрастает вплоть до критических значений, так как наибольшей температурой области насыщения является критическая температура. Параметры критической точки К: tкр = = 374 oC, Pкр = 22,1 МПа, vкр = 0,001 м3/кг. После пересечения с верхней пограничной кривой (х = 1) изобары, плавно сопрягаясь с прямолинейными отрезками области насыщения, начинают приобретать выпуклость, направленную вниз, а изотермы круто поворачивают направо, асимптотически стремясь к горизонталям. Последнее объясняется тем, что по мере удаления от области насыщения и падения давления перегретый пар по своим свойствам приближается к идеальному газу, для которого энтальпия является однозначной функцией температуры. С помощью h, s – диаграммы можно сразу с достаточной для инженерной практики точностью найти числовые значения для шести термодинамических параметров: h, s, v, p, t, x. Остальные необходимые термодинамические величины такие, как работа и теплота, а также изменение внутренней энергии, легко рассчитывают по найденным параметрам.
Диаграмма h-s приведена в приложении.
Рис. 1.6. h-s – диаграмма водяного пара Тема 1.2. Теплообмен Теория теплообмена изучает самопроизвольные необратимые процессы переноса теплоты в пространстве с неоднородным полем температуры. Под процессами переноса теплоты в теории теплообмена имеют в виду процесс обмена внутренней энергией между элементами системы в форме теплоты. Внутренняя энергия тел, имеющих более высокую температуру, убывает, а энергия тел с меньшей температурой увеличивается. Самопроизвольный процесс переноса теплоты в пространстве возникает под действием разности температур и направлен в сторону уменьшения темпе-ратуры. Закономерности переноса теплоты и количественные характеристики этого процесса исследуются в теории теплообмена. В природе существуют три основных способа переноса теплоты: теплопроводность, конвекция и тепловое излучение. Теплопроводность – молекулярный перенос теплоты при непосредственном соприкосновении молекул, атомов, ионов, свободных электронов с различными температурами. В чистом виде теплопроводность имеет место в твердых телах и неподвижных слоях жидкости и газа. Конвекция – процесс переноса теплоты, вещества, количества движения при перемещении в пространстве объемов жидкости или газа из области с одной температурой в область с другой температурой. Конвективный перенос теплоты всегда происходит вместе с теплопроводностью. Тепловое излучение – процесс распространения теплоты электромагнитными волнами. При этом внутренняя энергия тела (среды) переходит в энергию излучения. Тепловое излучение определяется только температурой и оптическими свойствами излучающего тела. В природе и технике элементарные процессы распространения теплоты – теплопроводность, конвекция и тепловое излучение очень часто происходят совместно. Конвективным теплообменом называется процесс совместного переноса теплоты конвекцией и теплопроводностью жидкости или газа. Конвективная теплоотдача (теплоотдача) – это конвективный тепло-обмен между потоками жидкости или газа и омываемой ими поверхностью. Тепломассообмен, обусловленный совместным переносом теплоты излучением и теплопроводностью, называют радиационно-кондуктивным. Если перенос теплоты осуществляется дополнительно и конвекцией, то такой процесс называют радиационно-конвективным.
Теплопередача – процесс теплообмена между двумя средами (жидкостью, газами) через разделяющую их поверхность, который осуществляется совмест-ным действием теплопроводности, конвекции и теплового излучения. Парогене-рирующие трубы котельного агрегата, например, получают теплоту от продуктов сгорания топлива в результате радиационно-конвективного теплообмена. Через слой наружного загрязнения, металлическую стенку и слой накипи теплота передается теплопроводностью. От внутренней поверхности трубы к омывающей ее воде теплота переносится теплоотдачей. Процессы теплообмена могут происходить в различных средах, чистых веществах и разных смесях, при изменении и без изменения агрегатного состояния жидкостей и т. д. В зависимости от этого теплообмен протекает по-разному и описывается различными уравнениями.
Теплопроводность Теплопроводностью называют молекулярный перенос теплоты микрочастицами, вызванный разностью температур. Процесс теплопроводности наблюдается в чистом виде в твердых телах. Молекулы, атомы, электроны и другие микрочастицы движутся со скоростями, пропорциональными их температуре. За счет взаимодействия друг с другом быстродвижующиеся микрочастицы отдают свою энергию более медленным, передавая таким образом теплоту из зоны с высокой в зону с более низкой температурой. Втвердых металлических телах теплопроводность происходит вследствие движения свободных электронов. Внеметаллических твердых телах(в частности, изоляционных материалах), в которых практически отсутствуют свободные электроны, перенос теплоты осуществляется за счет колебаний атомов и молекул. В газах микроструктурным движением является беспорядочные молекулярные движения, интенсивность которых возрастает с увеличением температур. В основе теории теплопроводности в твердых телах лежит закон Фурье:
где Q – количество переданной теплоты в единицу времени, Вт;
n – нормаль к изотермической поверхности тела; F – площадь, перпендикулярная к направлению распространения теплоты, м2; λ – коэффициент теплопроводности, Вт / (м · К). Коэффициент теплопроводности λ, характеризующий способность данного вещества проводить теплоту, зависит как от его природы, так и от агрегатного состояния. Значительное влияние на коэффциент теплопроводности могут оказывать температура, а у пористых материалов еще плотность и влажность. Значения λ для различных тел в зависимости от температуры приводятся в справочной литературе [3]. При исследовании процесса теплопроводности в твердых телах пользуются дифференциальным уравнением Фурье-Кирхгофа:
где Коэффициент температуропроводности является физической величиной, характеризующей скорость изменения температуры в данном веществе.
Если температурное поле не зависит от времени, то оно называется стационарным и описывается следующим уравнением:
Это уравнение является исходным при решении задач стационарной теплопроводности. Например, из этого уравнения получают выражение для температурных полей в однослойной стенке:
Здесь R – термическое сопротивление: - в случае плоской стенки
- в случае цилиндрической стенки
где δ – толщина плоской стенки; d2, d1 – внешний и внутренний диаметры цилиндра; t1, t2 – температура на внутренней и внешней поверхностях тела.
1.2.2. Конвективный теплообмен (теплоотдача) Общие положения. Конвективный теплообмен представляет собой сложный процесс, при котором теплота передается за счет перемещения объемов жидкости (газа) и одновременно за счет теплопроводности между неравномерно нагретыми частицами жидкости. Причиной конвективного теплообмена является неравномерность температурного поля внутри жидкой или газообразной среды (теплоносителя). Математический анализ конвективного теплообмена чрезвычайно сложен [1, 2]. Теплоотдача, характеризующая конвективный теплообмен между потоком
Закон Ньютона Практические расчеты теплоотдачи основываются на законе Ньютона-
где α - коэффициент теплоотдачи, характеризующий интенсивность процесса теплообмена. Размерность α - Вт/( Разность температур в соотношении (1.26) берут по абсолютной величине с учетом, что теплота распространяется самопроизвольно в сторону убывания температуры. Величина коэффициента теплоотдачи α сложным образом зависит от многих факторов: природы и режима движения, теплофизических свойств жидкости, температуры, формы и размеров поверхности теплообмена, ее положения в пространстве и др. По природе возникновения различают свободное (естественное) и вынужденное движение жидкости. Вынужденное движение создается внешними источниками (насосом, вентилятором и др.); свободное движение возникает за счет разности плотностей нагретых и холодных слоев жидкости, т. е. под действием архимедовых сил. Режим движения жидкости имеет решающее значение в процессах теплоотдачи, так как определяет физический механизм переноса теплоты. Различают два характерных режима движения - ламинарный и турбулентный. При ламинарном режиме частицы жидкости движутся по упорядоченным траекториям, вид которых определяется формой границ тела. Перенос теплоты осуществляется за счет соприкосновения частиц и слоев жидкости, т. е. за счет ее теплопроводности. В турбулентном режиме частицы жидкости движутся беспорядочно, по случайным траекториям, быстро меняющимся во времени, перенос теплоты происходит в основном за счет интенсивного перемещения частиц жидкости, т. е. за счет конвекции. Из курса гидрогазодинамики известно, что течение вязкой жидкости вдоль обтекаемой поверхности может быть ламинарным или турбулентным. Заторможенный слой у твердой поверхности называется пограничным. Внутри ламинарного слоя теплота переносится вследствие хаотического движения молекул, т. е. теплопроводностью жидкости. В турбулентном пограничном слое поперек него перемещаются и переносят теплоту крупные частицы жидкости, интенсивность теплообмена возрастает. Из многообразия физических свойств жидкости наибольшее влияние на процесс теплоотдачи оказывают следующие параметры: плотность ρж, кинематическая вязкость νж, коэффициент теплопроводности λж, температуропроводность аж, теплоемкость сж. Кроме того, коэффициент теплоотдачи зависит от скорости течения, от геометрических размеров, формы и положения тела. Задача расчета конвективного теплообмена - определение коэффициента
1.2.2.2. Основы теории подобия
При изучении конвективного теплообмена большую помощь оказывает теория подобия, на основе которой были установлены группы подобных явлений и обобщенные переменные - числа (критерии) подобия, характеризующие данную группу явлений. Эти числа подобия составляются из различных физических параметров, и они безразмерны. В случае конвективного теплообмена наиболее часто используются следующие числа подобия: ▪ число Нуссельта, определяющее интенсивность теплообмена:
▪ число Прандтля, характеризующее физические свойства жидкости:
▪ число Грасгофа характеризует интенсивность свободного движения:
▪ число Рейнольдса характеризует гидродинамический режим движения потока жидкости:
В эти выражения входят следующие величины:
l – определяющий размер тела, м;
g – ускорение свободного падения, м/с2; а – коэффициент температуропроводности жидкости, м2/с;
w – скорость потока жидкости, м/с. В зависимости от геометрической формы поверхности теплообмена в качестве определяющего размера l выбирают следующие параметры: • для труб и шаров определяющим линейным размером является • для вертикальных труб большого диаметра и пластин - высота Н; для горизонтальных плит – наименьший размер плиты(если греющая сторона плиты обращена вверх, то значение коэффициента α необходимо увеличить на 30 % по сравнению с приведенным, если греющая сторона обращена вниз, то значение Так как входящие в числа подобия физические величины зависят от температуры, значения этих чисел рассчитываются при температуре, называемой далее определяющей. Классификация задач по условиям конвективного теплообмена позволила выделить два основных вида конвективного теплообмена: ▪ теплообмен без изменения агрегатного состояния (вынужденная конвекция и свободная конвекция) жидкости; ▪ теплообмен при изменении агрегатного состояния(кипение и конденсация) жидкости. В свою очередь, каждый из этих видов конвективного теплообмена (кипение, конденсация, вынужденная и свободная конвекции) имеют свои разновидности. Для примера, можно показать порядок величины, α, Вт/(м2·К) для различных условий конвективного теплообмена:
В общем случае коэффициент теплоотдачи определяется как
При решении задач на конвективный теплообмен критерий Нуссельта чаще всего дается в критериальной форме в виде
где показатели степеней n1, n2, n3 и множитель пропорциональности Абыли найдены путем обработки экспериментальных данных.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 4947; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.89.2 (0.012 с.) |



 теплоемкости, которые имеют размерность: с, Дж/кг · К; с', Дж/нм3 · К;
теплоемкости, которые имеют размерность: с, Дж/кг · К; с', Дж/нм3 · К;  (1.15)
(1.15) соответствует бесконечно малому интервалу температур, а средняя -
соответствует бесконечно малому интервалу температур, а средняя -  конечному интервалу изменения температуры. Значения теплоемкостей основных газов приводятся в справочниках, учебных пособиях в зависимости от температуры [2, 3].
конечному интервалу изменения температуры. Значения теплоемкостей основных газов приводятся в справочниках, учебных пособиях в зависимости от температуры [2, 3]. Количество теплоты в термодинамическом процессе
Количество теплоты в термодинамическом процессе
 и учитывается работа сил внешнего давления dl´. Тогда согласно первому закону термодинамики
и учитывается работа сил внешнего давления dl´. Тогда согласно первому закону термодинамики

 (1.19)
(1.19) ,
, . (1.20)
. (1.20)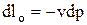 (знак минус указывает на уменьшение объема с ростом давления).
(знак минус указывает на уменьшение объема с ростом давления).

 , Дж.
, Дж.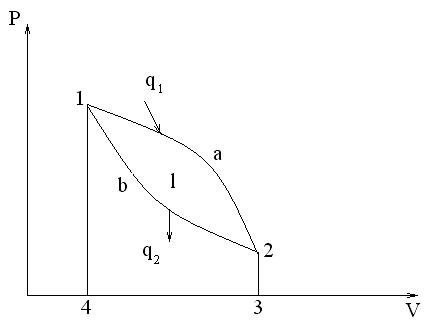
 . (1.21)
. (1.21) . (1.22)
. (1.22) не зависит от свойств рабочего тела, а его величина определяется температурами Т2 и Т1 холодного и горячего источников теплоты.
не зависит от свойств рабочего тела, а его величина определяется температурами Т2 и Т1 холодного и горячего источников теплоты.


 (1.23)
(1.23) - градиент температур, К/м;
- градиент температур, К/м; (1.24)
(1.24) - коэффициент температуропроводности, м2/с.
- коэффициент температуропроводности, м2/с.
 (1.25)
(1.25)

 , (1.26)
, (1.26) ), т. е. это - количество теплоты, которое в единицу времени отдается единицей поверхности тела при разности температур поверхности тела и омывающей среды в один градус.
), т. е. это - количество теплоты, которое в единицу времени отдается единицей поверхности тела при разности температур поверхности тела и омывающей среды в один градус. Величина α зависит от рядафакторов, влияющих на сам процесс теплообмена. К ним относятся скорость движения жидкости, физические свойства теплоносителя, гидродинамические характеристики потока, геометрическая форма и размеры поверхности теплообмена и др.:
Величина α зависит от рядафакторов, влияющих на сам процесс теплообмена. К ним относятся скорость движения жидкости, физические свойства теплоносителя, гидродинамические характеристики потока, геометрическая форма и размеры поверхности теплообмена и др.: ;
; ;
; ;
; .
. – коэффициент конвективной теплоотдачи, Вт/(м2·К);
– коэффициент конвективной теплоотдачи, Вт/(м2·К); – теплопроводность жидкости, Вт/(м2·К);
– теплопроводность жидкости, Вт/(м2·К); – кинематическая вязкость жидкости, м2/с;
– кинематическая вязкость жидкости, м2/с; – температурный коэффициент объемного расширения, 1/К (для газов
– температурный коэффициент объемного расширения, 1/К (для газов  , для жидкостей значения берутся из справочной литературы);
, для жидкостей значения берутся из справочной литературы); . (1.27)
. (1.27) , (1.28)
, (1.28)


